
математика Раздел1 практика
.pdf
минимума для функции S x . Поэтому в основании бака наименьшей площади должен лежать квадрат со стороной 4 м , высота бака должна быть
32 |
2 |
м . |
|
|
|||
42 |
|||
|
|
Задания для самостоятельного решения.
1.В треугольник с основанием a и высотой h вписан прямоугольник наибольшей площади. Определить площадь прямоугольника.
2.Забором длиной 120 м нужно огородить прилегающую к дому прямоугольную площадку наибольшей площади. Определить размеры прямоугольной площадки.
3.Разложить число 10 на два слагаемых так, чтобы произведение их было наибольшим.
График дифференцируемой функции называется выпуклым на
интервале a;b , если дуга кривой на этом интервале расположена ниже каса-
тельной, проведенной к графику функции в любой точке x a;b . Если на интервале a;b любая касательная располагается ниже дуги кривой графика функции, то он называется вогнутым на данном интервале. Точка
любая касательная располагается ниже дуги кривой графика функции, то он называется вогнутым на данном интервале. Точка
x0 ; f x0  , отделяющая участок вогнутости от участка выпуклости,
, отделяющая участок вогнутости от участка выпуклости,
называется точкой перегиба.
Теорема. (Достаточное условие выпуклости (вогнутости) графика функции.)
|
Если функция |
y f x дважды дифференцируема на интервале |
|||
a;b |
и для |
x |
a;b |
выполняется f '' x 0 |
( f '' x 0 ) , то функция |
выпукла (вогнута) на интервале a;b . |
|
||||
Прямая y |
kx |
b называется наклонной асимптотой графика функции |
|||
y |
f x , если расстояние от точки M x, f x |
до этой прямой стремится к |
|||
нулю при удалении точки М в бесконечность.
Практически параметры k,b наклонной асимптоты определяются из
k |
lim |
f |
x |
|
|
x |
. |
||
системы: |
x |
|||
|
|
|
||
b |
lim f |
x |
k x |
|
|
x |
|
|
|
|
|
|
|
71 |

Прямая x a является вертикальной асимптотой графика функции
y f x , если хотя бы один из односторонних пределов lim f |
x , lim f x |
x a 0 |
x a 0 |
равен бесконечности.
Пример. Определить промежутки выпуклости, вогнутости, точки перегиба
x2
функции y x2 1 .
Решение. Ранее была найдена первая производная этой функции
|
|
x2 |
' |
|
|
|
2x |
|
|
|
|
|
|
|
|
|
||||
y' |
|
|
|
|
|
|
|
|
|
|
. Найдѐм еѐ вторую производную: |
|
|
|||||||
x2 |
1 |
|
x2 |
1 2 |
|
|
||||||||||||||
y" |
|
|
|
2x |
' |
|
|
2 x2 1 2 |
2 x2 |
1 2x |
2x 6x2 |
2 |
|
|||||||
|
x2 1 |
2 |
|
|
|
|
|
|
x2 |
1 4 |
|
|
|
x2 |
1 3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y" 0 |
|
6x2 |
2 |
|
|
x2 |
1 0. |
|
|
|
|
|
|
|
|
|||||
|
x2 |
1 3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 |
1 |
0 |
|
x |
; 1 |
1; |
. Значит на промежутке x |
; 1 1; |
||||||||||||
график вогнутый. Аналогично, на |
1;1 |
y" 0 |
и график выпуклый. Точек |
|||||||||||||||||
перегиба нет, так как x |
1 и x |
1 не входят в ОДЗ. |
|
|
||||||||||||||||
Задания для самостоятельного решения.
Определить интервалы выпуклости, вогнутости, наличие точек перегиба.
1. |
y |
|
x |
4 |
|
4 |
|
x |
3 |
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
y |
|
|
e |
x2 |
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
y |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
y |
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
e x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. |
|
Определить асимптоты графика функции y |
x2 |
. |
|
|
||||||||||||||||||||||||||||||||||||
|
x2 |
1 |
|
|
||||||||||||||||||||||||||||||||||||||
Решение. |
|
Область определения функции: D( y) : |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
x |
, |
|
1 |
|
|
|
|
|
1; 1 |
1, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция не определена в точках x 1 и x |
1, поэтому эти точки являются |
|||||||||||||||||||||||||||||||||||||||||
точками разрыва функции y |
|
|
x 2 |
|
|
. Найдѐм односторонние пределы в этих |
||||||||||||||||||||||||||||||||||||
|
|
x 2 |
|
1 |
||||||||||||||||||||||||||||||||||||||
точках. |
lim |
|
|
|
x 2 |
|
|
1 |
|
, |
|
lim |
|
|
|
x 2 |
|
|
|
1 |
|
|
. Поэтому x |
|
1 – точка |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
1 0 x 2 |
|
1 |
0 |
|
|
|
x |
1 0 x 2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
разрыва 2 рода. Аналогично, |
|
lim |
|
|
|
|
x 2 |
|
|
|
1 |
|
|
|
|
, lim |
|
x 2 |
|
|
1 |
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 0 x 2 |
1 |
|
0 |
|
|
|
|
|
|
x 1 0 x 2 |
1 |
0 |
|
|
||||||||||||
Поэтому x 1 – точка разрыва 2 рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Раз x |
|
1 и x |
|
|
|
1 – точки разрыва 2 рода, то прямые - x |
1 и x |
1 |
|
|
||||||||||||||||||||||||||||||||
вертикальные асимптоты. Исследуем на наличие наклонной асимптоты:
72

|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k lim |
y |
|
lim |
x2 1 |
lim |
|
|
x2 |
|
0 , |
|
b lim y kx lim |
|
x2 |
|
|
0 x 1. |
|||||||||||
|
x |
|
x |
|
x |
|
|
|
x |
x |
x |
2 |
1 |
x |
|
x |
|
x |
x |
2 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поэтому y |
1 – наклонная асимптота. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Задания для самостоятельного решения. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Определить асимптоты графика функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1. |
|
y |
|
x |
e |
x |
|
|
|
|
2. |
|
y |
|
x2 |
4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
|
y |
|
x |
|
1 |
|
|
|
|
|
|
|
4. |
|
y |
|
x2 |
|
|
|
|
|
|
|
|||
|
|
|
2x |
|
3 |
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
28 Общая схема исследования функций и построение их графиков.
Полное исследование функции и схематическое построение еѐ графика обычно проводят по следующей схеме:
1.Область определения функции.
2.Исследование на чѐтность, нечѐтность, периодичность.
3.Наличие точек разрыва, поведение на 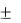 .
.
4.Наличие асимптот.
5.Точки пересечения графика с осями координат.
6.Интервалы монотонности, наличие точек экстремума.
7.Интервалы выпуклости, вогнутости графика функции и точки перегиба.
8.На основании проведѐнного исследования схематично строим график.
ПРИМЕР
Исследовать методами дифференциального исчисления функцию
y |
|
|
x |
и, используя результаты исследования, построить ее график. |
|||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
3 x 2 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
Решение |
|
|
|
|
|
|
|
||||
1) |
Область определения функции D(у) = ( , 1) ( 1,1) (1, ) . |
||||||||||
2) |
Область определения функции симметрична относительно нуля и |
||||||||||
выполняется равенство у(– х) = |
|
|
х |
|
|
= – у(х). Следовательно, функция |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
3 x2 |
|
1 |
|||||||||
|
|
|
|
|
|
|
|
||||
нечетная. Ее график симметричен относительно начала координат. Поэтому достаточно исследовать функцию в интервале 0,1 (1, ) .
Функция непериодическая.
3) Исследуем поведение функции на концах области определения. Функция не определена в точке х = 1. Следовательно, х = 1 точка разрыва функции.
73
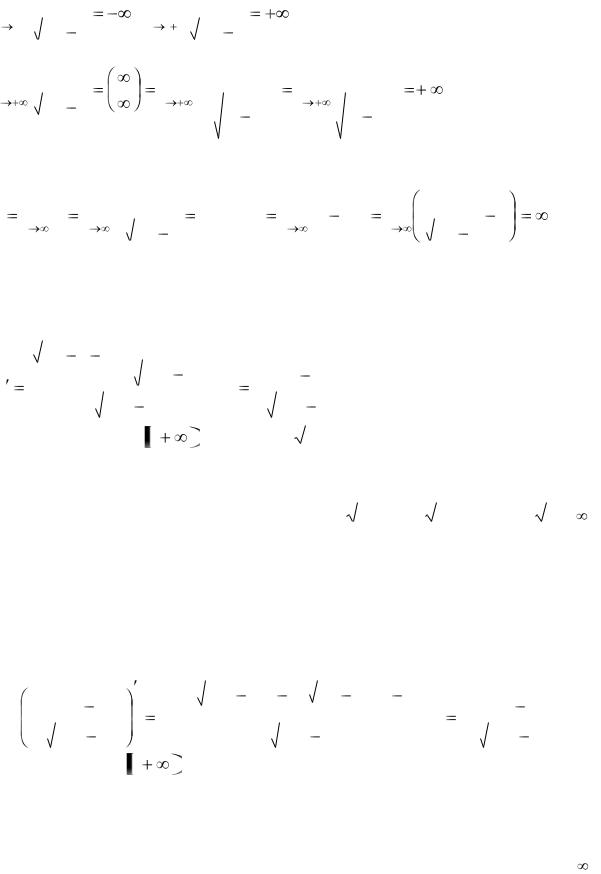
Определим характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:
х = 1
lim |
|
x |
; |
lim |
|
x |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
x 1-0 3 x2 1 |
|
x 1 0 3 x2 1 |
|||||||
значит, х = 1 – точка разрыва второго рода. |
|||||||||
lim |
|
|
x |
|
|
|
|
lim |
|
|
x |
|
|
|
lim |
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
x |
1 |
|
|
x |
1 |
|
1 |
|
|
x |
1 |
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x3 |
|
|
|
x |
|
x3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4) Прямая х = 1 является вертикальной асимптотой. Найдем наклонную асимптоту y = kx + b.
k lim |
y |
lim |
|
|
x |
|
|
0, |
b lim ( y kx) |
lim |
|
|
x |
|
|
0 |
. |
|
x |
|
3 |
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
2 |
|
|
|
2 |
|
|||||||||||
x |
x |
x |
x |
1 |
|
x |
x |
x |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
График данной функции наклонной асимптоты не имеет.
5)Точка пересечения графика данной функции с осями координат: О(0,0).
6)Определим интервалы возрастания, убывания функции и точки экстремума, для чего найдем у′:
3 |
|
|
x |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
x 2 1 |
|
|
|
|
|
2x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
3 |
(x |
2 |
|
1) |
2 |
|
|
|
|
x |
2 |
3 |
|
|
|||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1)2 |
|
|
|
|
|
|
33 (x 2 |
|
1)4 |
|||||||||||
|
|
|
3 (x 2 |
|
|
|
|
|
|
|
|
|
||||||||||
у′ = 0 в интервале |
0. |
|
|
|
в точке х = |
|
3 . |
|
|
|||||||||||||
Составим таблицу.
Таблица 1 – Исследование функции с помощью первой производной
х |
[0,1) |
1 |
|
|
|
|
|
|
|
|
|
(1, 3 ) |
3 |
( 3 ,+ ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
у′ |
– |
не сущест. |
– |
0 |
|
|
+ |
|
|
||
|
|
|
|
|
|
||||||
у |
убывает |
не сущест. |
убывает |
уmin≈1,37 |
возраст. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
7) Определим интервалы выпуклости, вогнутости графика функции и точки перегиба.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
|
2x3 (x |
2 |
1) |
4 |
x |
2 |
|
1(x |
2 |
3)2x |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
у″= |
1 x |
3 |
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
1 2x(9 x |
) |
. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 3 |
|
|
|
|
|
|
|
||||||||||
3 |
(x |
2 |
1) |
4 |
|
|
|
|
|
|
|
|
3 |
|
(x |
2 |
1) |
8 |
|
|
|
|
|
(x |
2 |
1) |
7 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
На промежутке 0. |
|
|
|
у″ обращается в нуль в точках х = 0, х = 3 и не |
|
|||||||||||||||||||||||||||||||||||||||||||
существует в точке х = 1. у(3) = |
|
3 |
|
. Составим таблицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таблица 2 – Исследование функции с помощью второй производной |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
х |
|
|
|
0 |
|
|
|
|
|
(0,1) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(1,3) |
|
|
3 |
|
|
|
|
|
|
|
(3,+ |
) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
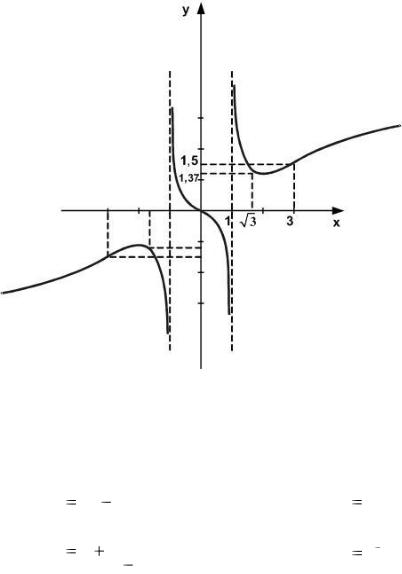
у″ |
0 |
– |
не сущ. |
+ |
0 |
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
у |
упер.= 0 |
выпукл. |
не сущ. |
вогнут. |
упер.= |
3 |
|
выпукл. |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
8) Используя результаты исследования, строим график функции (рисунок 1).
Рисунок – График функции Задания для самостоятельного решения.
Провести полное исследование указанных функций и построить их графики:
1. |
y |
x |
3 |
3x |
2 |
|
2. |
y |
|
x |
|
|
|
|
|
||||||||
|
|
|
|
|
ln x |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
3. |
y |
x |
|
1 |
|
|
4. |
y |
e |
x2 |
|
|
|
x |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
29 Примеры функций нескольких переменных. Область определения, график. Предел и непрерывность функции 2 переменных. Частные производные функций нескольких переменных. Полный дифференциал функций двух переменных и его применение к приближѐнным вычислениям.
Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных z = f(x, y). Если аргументов более 2, то говорят про ФНП.
75

Пример. |
z |
|
x |
|
, z x y |
, z sin x y и т. д. |
|
|
|
|
|||||
y |
v |
u |
|||||
|
|
|
|
Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие
MM0 r
также верно и условие |
f (x, y) A |
. |
|
|
|
Записывают: lim f (x, y) A
xx0
yy0
Определение: Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется
непрерывной в точке М0(х0, у0), если lim f (x, y) f (x0 , y0 ) , причѐм точка |
|
x |
x0 |
y |
y0 |
М(х, у) стремится к точке М0(х0, у0) произвольным образом.
В противном случае говорят о точках разрыва ФНП.
Пример. Найти область определения функции z |
1 |
. |
|
||
x2 y 2 1 |
Решение. Функция определена во всех точках координатной плоскости, за исключением точек удовлетворяющих условию x2 y2 1 0 . Очевидно, что
этому условию удовлетворяют все точки, лежащие на окружности единичного радиуса с центром в начале координат. Поэтому область
определения функции |
z |
|
1 |
|
|
есть вся координатная плоскость за |
|
|
|
|
|
||||
x2 |
y 2 |
1 |
|||||
|
|
|
|||||
исключением точек этой окружности.
Задания для самостоятельного решения.
Найти область определения функций нескольких переменных.
1. |
|
|
|
|
|
2. |
z ln x y2 |
|||
z |
|
25 x2 y2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
3. |
z |
1 |
|
|
4. |
z sin |
x |
2 |
|
|
|
|
|
|
|
|
|
||||
|
2x 3y |
|
|
y |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
76

Пример. Исследовать на непрерывность функцию z |
|
x2 |
|
3y2 |
в точке 0;0 . |
|
x2 |
y2 |
|||
|
|
|
|||
Решение. Приближаясь к точке 0;0 вдоль прямой y |
|
kx , получим: |
|||
lim |
x2 |
|
3y2 |
|
lim |
x2 |
3k 2 |
|
x2 |
|
lim |
x2 1 3k 2 |
|
|
lim |
|
1 3k 2 |
|
|
|
1 3k 2 |
|
. Если |
|||||||||||||||||||||
x2 |
|
y2 |
|
x2 |
k 2 |
x2 |
|
x2 1 k 2 |
|
|
|
1 k 2 |
|
|
1 k 2 |
|||||||||||||||||||||||||||||
x 0 |
|
|
x 0 |
|
x 0 |
|
|
x 0 |
|
|
|
|||||||||||||||||||||||||||||||||
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бы предел функции |
z |
|
x |
2 |
3y2 |
|
в точке |
0;0 |
|
существовал, то он был бы |
||||||||||||||||||||||||||||||||||
|
x2 |
|
y2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
единственным и не зависел от направления подхода к точке |
|
|
0;0 . Раз |
|||||||||||||||||||||||||||||||||||||||||
зависимость от k есть, то lim |
|
x2 |
|
3y2 |
|
не существует. Значит, по |
|
|||||||||||||||||||||||||||||||||||||
|
x2 |
|
|
y2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определению точка |
0;0 |
|
|
|
– точка разрыва функции |
z |
|
x2 3y2 |
. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
x2 |
y2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задания для самостоятельного решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Исследовать на непрерывность функцию z |
z x; y |
в точке. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x 3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
x2 |
y2 |
|
|
; |
|
|
|
||||||||
1. |
|
|
z |
|
|
; |
0;0 |
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
4 |
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Определение. Пусть в некоторой области задана функция z = f(x, y). |
|
|||||||||||||||||||||||||||||||||||||||||||
Возьмем произвольную точку М(х, у) и зададим приращение |
|
х к |
|
|||||||||||||||||||||||||||||||||||||||||
переменной х. Тогда величина |
xz = f( x + x, y) – f(x, y) называется |
|
||||||||||||||||||||||||||||||||||||||||||
частным приращением функции по х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Тогда |
lim |
|
x z |
|
|
lim |
|
f (x |
|
|
|
x, y) |
f (x, y) |
называется частной производной |
||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
x |
0 |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
функции z = f(x, y) по х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Обозначение: |
|
z |
; |
zx ; |
|
|
f (x, y) |
; |
|
f x (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично определяется частная производная функции по у.
z |
lim |
f (x, y |
y) f (x, y) |
|
y |
|
y |
||
y 0 |
||||
|
|
|||
Частные производные ФНП ищутся с соблюдением всех известных правил дифференцирования. При этом при дифференцировании по одной переменной остальные переменные зафиксированы, то есть считаются постоянными.
Пример. Найти частные производные заданной ФНП в произвольной точке: z x y .
77

Решение. При дифференцировании по переменной x функция z |
x y |
|||||
является степенной. Тогда |
z |
y x y 1 . При дифференцировании по |
||||
x |
||||||
|
|
|
|
|
||
переменной y функция z |
x y является показательной и производная ищется |
|||||
по правилу дифференцирования показательной функции: |
z |
x y |
ln x . |
|||
y |
||||||
|
|
|
|
|
||
Задания для самостоятельного решения.
Найти частные производные заданной ФНП в произвольной точке.
1. |
z |
y |
2 |
e |
x2 |
|
|
|
2. |
z |
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
z |
ln 1 |
|
x |
2 |
y |
2 |
4. |
|
|
|
|
|
|
|
z |
tg x |
y |
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у приращения функции z в точке (х,
у).
dz  f x (x, y)dx f y (x, y)dy
f x (x, y)dx f y (x, y)dy
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
Пример. Найти полный дифференциал функции z |
|
|
|
|
. |
|||||||||||||||||||||||||||||||
|
|
x 2 |
y 2 |
|||||||||||||||||||||||||||||||||
Решение. |
|
z |
|
|
|
2 yx |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
(x2 y 2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z y (x2 |
|
y 2 ) y( 2 y) |
|
x2 |
y 2 |
|
|
|
|
2 y 2 |
|
|
|
|
x2 |
y 2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||
|
y |
|
|
(x2 |
y 2 )2 |
|
|
|
|
|
(x2 |
y 2 )2 |
|
|
|
(x2 |
y 2 )2 |
|
|
|||||||||||||||||
|
|
|
|
2xy |
|
|
|
x2 |
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dz |
|
|
|
dx |
|
|
|
|
|
|
dy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(x2 |
y 2 ) |
|
(x2 |
|
y 2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Приближѐнные вычисления основаны на формуле: |
|
|
||||||||||||||||||||||||||||||||||
|
f (x |
|
x, y y) |
f (x, y) |
|
|
f (x, y) |
|
x |
|
|
f (x, y) |
y . |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Вычислить приближенно значение 1,041,99 . |
|
|
||||||||||||||||||||||||||||||||||
Решение. Здесь z |
|
x y , |
|
z |
|
|
y |
x y |
1 , |
|
z |
|
|
x y ln x , |
x; y |
1;2 , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
|
|
|
y |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x; |
y |
0,04; |
0,01 . В соответствии с формулой |
|
|
|
|
|
|||||||||||||||||||||||||||
1,041,99 12 |
2 11 |
|
0,04 |
12 |
|
ln1 |
0,01 |
|
1 0,08 0 1,08. |
|
||||||||||||||||||||||||||
Задания для самостоятельного решения. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Вычислить приближѐнно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
|
1,023,01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,022 |
2,982 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|
|
||

3. |
1,023 2,953 |
4. |
arctg |
1,99 |
1 |
|
0,97 |
||||||
|
|
|
|
|
||
|
|
|
|
|
|
30 Нахождение экстремумов функции двух переменных.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
f (x0 , y0 ) f (x, y) ( f (x0 , y0 ) f (x, y) )
то точка М0 называется точкой максимума (минимума).
При нахождении точек экстремума Ф2П используются следующие факты:
Теорема. (Необходимые условия экстремума).
Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю
fx (x0 , y0 ) 0, f y (x0 , y0 ) 0 , либо хотя бы одна из них не существует.
Точку (х0, у0) будем называть критической точкой.
Теорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
D x, y |
f |
x |
2 (x, y) |
f xy (x, y) |
|
A B |
|
A C B2 . |
|
|
|
||||||||
|
|
|
2 (x, y) |
|
|
|
|||
|
f xy (x, y) |
f |
|
B C |
|
|
|||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум. При этом если f x2 (x0 , y0 ) 0 , то в точке (х0, у0) будет максимум, если же
f x2 (x0 , y0 ) 0 - минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума В случае, если D = 0, вывод о наличии экстремума сделать нельзя.
Пример Найти экстремумы функции f (x, y) 1 15x 2x 2 xy 2 y 2 .
Решение. Функция определена на всей координатной плоскости. Найдѐм частные производные первого порядка, приравняем их к нулю и решим систему уравнений:
f 'x (x, y) 0 |
15 4x y 0 |
15 15y 0 |
y |
1 |
. |
|
f ' y (x, y) 0 |
x 4y 0 |
x |
4 y |
x 4 |
|
|
|
|
|||||
Значит, стационарная точка M(4;-1). Находим частные производные второго порядка:
f ' 'xx (x, y) (15 4x y)'x |
4 ; |
79

f ' ' yy (x, y) ( x 4y)' y |
4 ; |
|
|
|
|
|
|
|
|
||
f ' 'xy (x, y) |
(15 4x y)'y |
1. |
|
|
|
|
|
|
|
|
|
В данном случае производные от x, y не зависят, поэтому и для |
|||||||||||
стационарной точки M(4;-1) имеем: |
|
f ' 'xx (4; |
1) 4 ; f ' ' yy (4; |
1) 4 ; |
|||||||
f ' 'xy (4; 1) |
1. Тогда |
|
A |
B |
|
4 |
1 |
|
15 0 |
. Так как A 0 |
, то M(4;-1) – |
|
|
|
|||||||||
|
B |
C |
|
1 |
4 |
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
точка локального максимума исходной функции. Максимум функции
f (x, y) |
1 15x 2x 2 |
|
xy |
2 y 2 будет |
fmax |
f (4; 1) 31. |
|
|
||
Задания для самостоятельного решения. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1. |
|
f (x, y) |
x 2 |
xy |
y 2 |
10 |
2. |
f (x, y) (x 3)2 |
y 1 2 |
1 |
3. |
|
f (x, y) |
3x 6 y |
x2 |
xy y 2 |
4. |
f (x, y) 2x3 xy 2 |
5x2 |
y 2 |
|
31, 32 Алгебраическая, тригонометрическая и показательная формы комплексного числа, его геометрическая интерпретация. Действия над комплексными числами. Извлечение корней натуральной степени из комплексного числа
Определение. Алгебраической формой комплексного числа z
называется выражение z a ib , где |
a и b – действительные числа, |
|
i – |
|||
мнимая единица, которая определяется |
соотношением: i 2 |
|
|
|
|
|
1; |
i |
1. |
||||
При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа z a ib и z a ib называются комплексно –
сопряженными.
Любое комплексное число представляется точкой на (комплексной) плоскости. Координатами этой точки будут соответственно действительная и мнимая части комплексного числа.
С помощью геометрического представления комплексные числа можно представлять в тригонометрической форме: z a ib r(cos
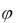
80
