
- •3. Синтез и анализ зубчатой передачи и планетарного редуктора.
- •3.1. Цели и задачи третьего листа. Классификация зубчатых механизмов с неподвижными осями; основные теоремы зацепления.
- •3.2. Геометрический расчёт рядовой цилиндрической зубчатой передачи.
- •3.3. Построение картины эвольвентного зацепления. С.429-432[1].
- •3.4. Построение зубчатого зацепления; определение активных профилей зубьев; определение активной линии зацепления и коэффициента торцового перекрытия аналитическим и графическим способами
- •3.5.Метод нарезания эвольвентных профилей зубьев.
- •3.6. Определение общего передаточного отношения заданного привода, а также простой и планетарной ступени зубчатого механизма.
- •3.7. Построение плана линейных скоростей.
- •3.8. Построение плана частот вращения зубчатых колёс. Определение частоты вращения зубчатых колёс аналитическим методом.
3. Синтез и анализ зубчатой передачи и планетарного редуктора.
3.1. Цели и задачи третьего листа. Классификация зубчатых механизмов с неподвижными осями; основные теоремы зацепления.
При выполнении 3-го листа надо спроектировать эвольвентное зацепление, исходя из заданного передаточного отношения (основное условие). В качестве дополнительных условий при проектировании зубчатой передачи необходимо выполнение следующих условий:
отсутствие подрезание ножки зуба.
обеспечение непрерывности зацепления.
обеспечение отсутствия заострения головки зуба.
отсутствие интерференции зубьев.
При проектировании планетарного механизма необходимо подобрать число зубьев зубчатых колёс, исходя из основного условия заданного передаточного отношения. В качестве дополнительного условия будем использовать условие соосности.
Зубчатое зацепление – высшая кинематическая пара, образованная последовательно взаимодействующими зубцами двух колёс.
Зубчатые механизмы с неподвижными осями делятся на три группы:
с параллельными осями (цилиндрические);
с пересекающимися осями (конические);
с перекрещиваюмися осями (гиперболические);
В зависимости от формы зуба передачи бывают: эвольвентного зацепления, зацепления Новикова, цевочного зацепления, зацепление циклоидное и цевочное зацепление.
В зависимости от
направления зуба: прямоугольная,
косозубая (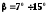 ),
шевронная (
),
шевронная (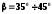 ).
).
Взаимодействующие поверхности зубцов, обеспечивающие заданное передаточное отношение, называется сопряжёнными поверхностями.
Передаточное отношение зубчатого механизма – отношение угловой скорости входного звена к угловой скорости выходного звена:
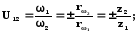 с.139 [1]
с.139 [1]
где rw1 и rw2 – радиусы начальных окружностей колёс;
z1 и z2 – число зубьев колёс.
(-) – внешнее зацепление (в разные стороны);
(+) – внутренне зацепление (вращение зубчатых колёс в одну сторону), (передаточное отношение – отношение числа зубьев большего колеса к числу зубьев меньшего колеса – шестерни; не всегда совпадает с передаточным отношением).
Задача синтеза внутреннего зацепления состоит в определении сопряжённых поверхностей зубцов по заданному относительному движению (передаточному отношению).
При воспроизведении возвратного движения можно иметь одну пару сопряжённых поверхностей. Если же требуется воспроизвести непрерывное движение в одном направлении, то надо иметь несколько последовательно взаимодействующих пар сопряжённых поверхностей, которые располагаются на выступах, называемых зубьями. Для полного зацепления вместо сопряжённых поверхностей можно рассматривать сопряжённые профили, т.е. кривые, получаемые в сечении сопряжённых поверхностей плоскостью, параллельной плоскости движения.
Связь меду заданными законами относительного движения и геометрическими характеристиками сопряжённых поверхностей устанавливается основной теоремой зацепления:
Сопряжённые поверхности должны быть выбраны так, чтобы в любой точке их контакта, общая нормаль к ним была перпендикулярно вектору скорости точки контакта в заданном относительном движении поверхностей.
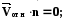
где
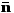 - единичный орт по нормали;
- единичный орт по нормали;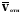 - вектор скорости точки контакта (к)
сопряженных поверхностей в движении
одного звена относительно другого.
- вектор скорости точки контакта (к)
сопряженных поверхностей в движении
одного звена относительно другого.
Зацепление в котором оба звена совершают движение в одной и той же плоскости называется плоским.
Теорема для плоского зацепления:
Для передачи вращения с заданным передаточным отношением необходимо, чтобы общая нормаль к профилям зубьев в точке их контакта (касания) делила межосевое расстояние на части обратнопропорциональные угловым скоростям.
Если
 - полюс зацепления, геометрические места
точек на звеньях 1 и 2, которые при их
движении последовательно совпадают с
полюсом зацепления образую центроиды
Ц1
и Ц2
(центральный механизм – простейший
механизм для преобразования вращательного
движения вокруг одной оси во вращательное
движение вокруг другой оси); если
- полюс зацепления, геометрические места
точек на звеньях 1 и 2, которые при их
движении последовательно совпадают с
полюсом зацепления образую центроиды
Ц1
и Ц2
(центральный механизм – простейший
механизм для преобразования вращательного
движения вокруг одной оси во вращательное
движение вокруг другой оси); если
 ,
то Ц1
и Ц2
– окружности радиусов rw1
и rw2).
,
то Ц1
и Ц2
– окружности радиусов rw1
и rw2).
