Глава 2. Напряжённо-деформированное состояние стержня при центральном растяжении (сжатии).

1.Внутренние силовые факторы.

Yℓ+∆ℓ

А а` а с с` В

PP

Z

b`bdd`

ℓ

Рис.2.1

Рассмотрим стрежень АВ, по торцам которого действуют силы Р, растягивающие его (рис.2.1).

Для установления вида напряженного состояния применим метод плоских сечений и определим внутренние силовые факторы (рис.2.2).

A

N(z) Z

Рис.2.2

Ограничимся рассмотрением случая, когда внешние силы Р приложены в центрах тяжестей торцевых сечений. Из рис.2.2 очевидно, что из всех внутренних силовых факторов отличной от нуля будет только нормальная сила N(z), приложенная в центре тяжести мысленного поперечного сечения. В этом случае имеет место так называемое центральное растяжение.

Условимся направлять нормальную силу по направлению внешней нормали. Составим уравнение равновесия:

- P+N(z)= 0

Откуда получаем : N(z)=P

Аналогично можно рассуждать в случае, когда пара сил Р сжимают стержень. В этом случае величину N(z) получим с отрицательным знаком.

Таким образом отличие растяжения и сжатия будет сказываться только в знаках. Знак плюс нормальной силы указывает на растяжение, знак минус – на сжатие.

2.Напряжения при растяжении – сжатии стержня.

Из определения понятий о напряжениях следует, что от действия нормальной силы возникают нормальные напряжения. При этом условимся, что по толщине стержня напряжения и деформации остаются неизменными. То есть, фактически можно ограничиться по определению напряжений по высоте поперечного сечения в плоскости поперечного сечения.

Закон распределения напряжений по сечению стержня можно представить различными способами: см. рис.2.3, 2.4 и 2.5

Z

N(z)

Рис.2.3

Z

N(z)

Рис.2.4

Z

N(z)

Рис.2.5

Примеры использования принципа Сен-Венана изображены на рис. 2.3 – 2.5. Принцип Сен-Венана позволяет получать приближённые решения задач теории упругости с помощью решения аналогичных задач для частных распределений действующих сил.

Введём понятия продольной деформации и продольного напряжения в соответствии с формулами (2.1) и (2.3). В сопротивлении материалов мы имеем дело с малыми упругими деформациями для которых справедлив закон Гука (см. 2.2).

Для установления закона распределения нормальных напряжений составим условие совместности деформации. Для этого воспользуемся гипотезой плоских сечений Бернулли .

Рассмотрим стержень постоянного поперечного сечения аbиcd.

ℓ(y)=const.

По гипотезе плоских сечений при растяжении эти сечения не искривятся и переместятся параллельно себе. В результате новое расстояние будет:

(ℓ+∆ℓ)(у)=const.

Абсолютное удлинение :

(ℓ+∆ℓ)(у)-ℓ(у)=∆ℓ(у)=const.

Относительное удлинение – деформация :

(2.1)

Используя закон Гука, связывающий напряжения с деформацией линейной зависимостью :

(2.2)

Где Е – модуль упругости (модуль Юнга).

Таким образом по сечению стержня нормальные напряжения распределяются равномерно (рис.2.5).

Согласно определению нормального напряжения

(2.3)

Можем записать :

Так как , эту величину можно вынести из под знака интеграла :

То есть :

Откуда окончательно :

(2.4)

При расчётах на жесткость при растяжении – сжатии требуется определять величину удлинения стержня под нагрузкой. Закон Гука можем записать следующим образом :

Подставляя значения напряжения и деформации, перепишем закон Гука :

где ℓ - длина стержня.

Отсюда выражение для удлинения ∆ℓ :

(2.5)

Таким образом, получили выражение для удлинения (укорочения) стержня при растяжении (сжатии). Жесткость стержня характеризуется произведением , которое так и называется «жесткость при растяжении – сжатии».

Расчеты на прочность при растяжении – сжатии.

Из формулы (2.4) следуют три рода задач, решаемые при растяжении – сжатии. Составляется уравнение прочности для наиболее опасного сечения :

где- допускаемое напряжение. (2.6)

Допускаемое напряжение определяется через механические характеристики материала.

- для пластичных материалов,

- для хрупких материалов,

Где - предел текучести,

- предел прочности, обе эти величины получают путем механических испытаний материала,

n– коэффициент запаса прочности, назначается в зависимости от рода материала, способа приложения нагрузки и степени ответственности детали.

Определение допускаемой нагрузки. Для расчётного «опасного» сечения определяется допускаемое значение внутреннего силового фактора :

В конкретных задачах существует однозначная связь величины с величиной внешней нагрузки. Таким образом, определяется величина допускаемой нагрузки.

Энергетический метод расчёта на прочность. Рассчитывается величина внутренней потенциальной энергии упругой деформации тела.

Внутренняя потенциальная энергия упругой деформации при растяжении – сжатии.

Энергия упругой деформации (U) подсчитывается в предположении, что нагрузка прикладывается статически. При этом работа внешних сил полностью переходит в потенциальную энергию упругой деформации. Процесс нагружения складывается следующим образом. При отсутствии нагрузки удлинение отсутствует. Чем больше нагрузка, тем больше удлинение стержня. Графически зависимость между статически прикладываемой нагрузкой и удлинением стержня можно представить в виде прямой в соответствии с законом Гука, см рис.2.6

P

0. ∆ℓ

Рис.2.6

Работа А определяется как площадь под кривой процесса:

Внутренняя энергия : U=A

Учитывая, что нормальная сила возникает от действия силы Р, можем записать :

Подставляя из формулы (2.5) значение величины ∆ℓ, получим :

Для стержня, состоящего из nучастков, окончательно получаем :

Удельная потенциальная энергия определяется как энергия, отнесённая к единице объёма V:

Где .

Удельную энергию можем определить следующим образом :

При этом : ;.

Энергетическая гипотеза прочности. Здесь «опасным» считается такое состояние, когда удельная потенциальная энергия элемента начнёт превышать допускаемое при простом центральном растяжении:

Пример.

Стержень переменного сечения жестко защемлен в концевых сечениях и нагружен силой Р.

Требуется :

1. Определить реакции в заделках.

2. Построить эпюры нормальных сил N(z), нормальных напряжений, деформациии перемещенийw(z). Для этого составить на каждом участке соответствующие аналитические выражения и определить в буквенном виде значения характерных ординат.

3. Определить из условия прочности допускаемую величину силы Р.

4. Определить энергию деформации двумя способами :

а) как работу внешних сил,

б) вычислить энергию деформации, используя аналитические выражения нормальных сил N(z).

Данные к задаче :

a=0.1м;;

Примечания :

1. эпюра – это график исследуемой величины по оси стержня или по его поперечному сечению;

2. в нашем случае рассматривается задача когда напряжения и деформации по толщине стержня не меняются; и эпюры напряжений и деформаций строятся только по оси стержня.

Решение.

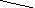
А В С 3 участок Д

1 участок 3F

F P Z

2a a 4a

Рис.2.7

Обозначаем характерные сечения начальными буквами латинского алфавита. Проводим продольную ось Z. см.рис.2.7. Отбрасываем мысленно заделку и заменяем на действия реакциямиR_A иR_Д, направляя обе в стороны, противоположные направлению силы Р. Удобно на этой схеме провести оси будущих эпюр.

Составляем уравнение равновесия : ,R_A+R_Д=P

Остальные уравнения равновесия дают тождественный ноль.

Таким образом, получаем одно уравнение с двумя неизвестными. Для решения поставленной задачи не достаёт одного уравнения, значит задача один раз статически неопределимая. Составим уравнения совместности перемещений, воспользовавшись законом Гука и принципом независимости действия сил.

Мысленно отбросим связь заделки в сечении А, заменив её действие силой R_A. При этом опораDсохраняется. Перемещение сечения А к сечениюDпод действием силыR_Aбудет равно :

При этом, жёсткость на 2 и 3 участках одинаковы, поэтому для 2 и 3 участков составляется общее слагаемое. Далее сечение освободим от нагрузки . Тогда перемещение сечения С к сечению D будет равно:

После простейших арифметических действий получаем :

Данный класс задач удобнее решать в простых дробях, что позволяет получать конечный результат в абсолютном значении без всяких приближений.

Аналогичные рассуждения в отношении правой реакции опоры приводят к результату

R д =7/11 P

Легко проверить, что при этом уравнение равновесия выполняется.

Построение эпюр.

Принято строить эпюры на недеформированном стержне.

Участок АВ . Мысленно делим стержень на 2 части и отбрасываем правую часть. Рассматриваем равновесие левой части. Мысленно направляем нормальную силу по внешней нормали и записываем уравнение равновесия левой части:

N(Z1) + Ra = 0 ;

То же отсечение левой части проводим на участке ВС, для которого условие равновесия имеет такой же вид, как и для

участка АВ. Таким образом нормальная сила на участках АВ и СD одинакова по величине и направлению (сжатие).

На участке CD стержень испытывает растяжение, так как из уравнения равновесия левой части стержня (при сечении

участка CD) следует:

N(Z3) = P – Ra > 0

Используя определение (2.4) для каждого из трёх участков определяем нормальные напряжения и строим

эпюру. Из закона Гука (2.2) определяем значения деформаций.

Строим эпюру нормальной силы

Эпюра перемещений W(Z).

Так как в пределах каждого участка деформации постоянны, то для построения эп.ры перемещений достаточно определить значения перемещений на границах участков и соединить эти координаты прямыми.

В сечении А перемещение отсутствует:

W(A)=0

В сечении В перемещение определяется деформацией первого участка:

и т.д.