
Использование замены переменной
Задача. Найти
![]()
Решение:
Обозначим
![]() .
Тогда для дифференциала данной функции
имеем выражение
.
Тогда для дифференциала данной функции
имеем выражение
![]() .
Следовательно
.
Следовательно
![]()
Подставляя в исходное выражение, получаем
![]() .
.
Иногда не вводят
обозначение для новой переменной, а все
выражение для новой переменной через
старую используют как ее имя, записывая
это выражение под знаком дифференциала.
Это и называют «подведением под знак
дифференциала». В рассмотренном примере:
![]() ,
мы можем записать
,
мы можем записать
![]() .
.
Задача. Найти
 .
.
Решение:
Обозначим
![]() .
Тогда
.
Тогда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Получаем

![]() .
.
Задача. Найти

Решение:
Обозначим
![]() .
Тогда
.
Тогда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Получаем
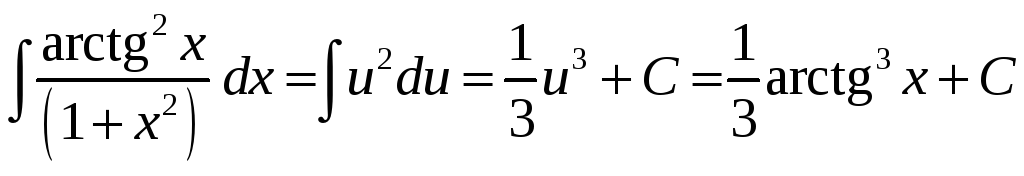 .
.
Вычисление
интегралов вида
![]() .
.
Метод вычисления таких интегралов изложим на примере:
Задача. Найти
![]()
Решение:
Выделим полный квадрат в знаменателе:
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.

В первом интеграле
сделаем замену:
![]() .
.
Тогда
![]() .
Второй интеграл табличный.
.
Второй интеграл табличный.
Получаем:

Ответ:
![]()
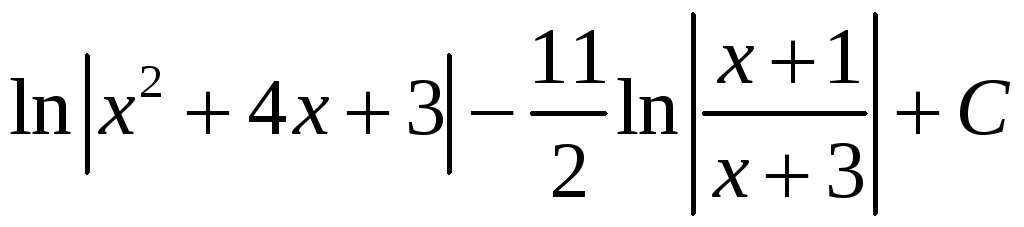 .
.
Задача. Найти
![]()
Ответ:
![]()
![]() .
.
Задача.
Найти
![]()
Ответ:
![]() =
=![]() .
.
Вычисление
интегралов вида
 .
.
Технология здесь аналогична рассмотренной в предыдущем случае.
Задача. Найти
 .
.
Решение:
Выделим полный
квадрат в подкоренном выражении в
знаменателе:
![]() ,
сделаем замену
,
сделаем замену
![]() .
.
Получаем

В первом интеграле
сделаем замену:
![]() .
.
Тогда
![]() .
Второй интеграл табличный.
.
Второй интеграл табличный.
 .
.
Ответ:

![]() .
.
Задача. Найти
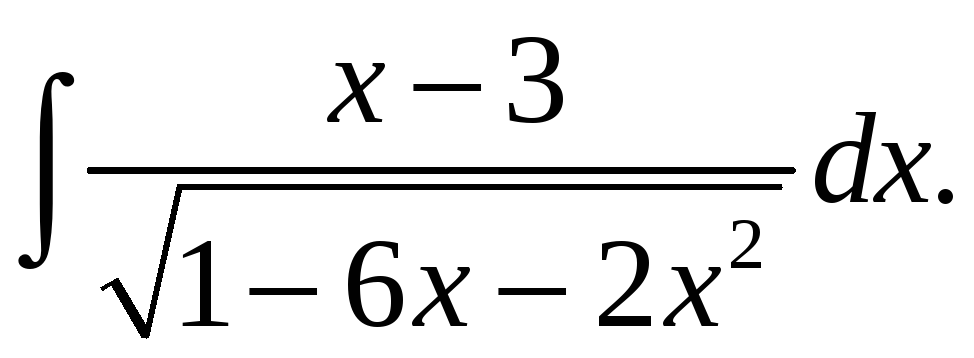
Указание:
Выделите полный
квадрат в знаменателе:

 .
.
Ответ:

![]() .
.
Применение формулы интегрирования по частям для вычисления неопределенных интегралов.
Формула интегрирования по частям имеет вид
![]()
В этой формуле за
![]() и
и
![]() обозначены
дифференциалы некоторых функций.
обозначены
дифференциалы некоторых функций.
На всякий случай
еще раз напомним определение дифференциала
функции
![]() ,
а так же формулу восстановления функции
по ее дифференциалу
,
а так же формулу восстановления функции
по ее дифференциалу
![]() .
.
Задача. Найти![]() .
.
При использовании
формулы интегрирования по частям важно
правильно на первом этапе разбить
подынтегральное выражение на два
множителя
![]() и
и
![]() .
Неудачное разбиение может привести не
к упрощению, а, наоборот, к усложнению
примера. В указанном примере обозначим
.
Неудачное разбиение может привести не
к упрощению, а, наоборот, к усложнению
примера. В указанном примере обозначим
![]() .
Всю оставшуюся часть подынтегрального
выражения мы обозначим
.
Всю оставшуюся часть подынтегрального
выражения мы обозначим
![]() ,
то есть
,
то есть
![]() .
.
Тогда имеем:
![]()
![]() ;
;
![]() .
.
Применяя формулу интегрирования по частям, получаем
 .
.
Для вычисления последнего интеграла подынтегральное выражение преобразуем к виду

Тогда получаем

![]() .
.
Ответ:
![]() .
.
Формула интегрирования «по частям» применяется для вычисления
интегралов
вида:
![]() ;
;
![]() ;
;
![]() .
.
Где
![]() - многочлен степени
- многочлен степени
![]() .
При вычислении таких интегралов
принимается
.
При вычислении таких интегралов
принимается
![]() .
.
Отметим, что тогда:
1)![]() ,
то есть
,
то есть
![]() ;
;
2)
![]() ,
то есть
,
то есть
![]() ;
;
3)
![]() ,
то есть
,
то есть
![]() .
.
Задача. Найти
![]() .
.
Полагаем
![]() ,
следовательно
,
следовательно
![]() .
Тогда
.
Тогда
![]() .
.
Применяя формулу интегрирования по частям, получаем
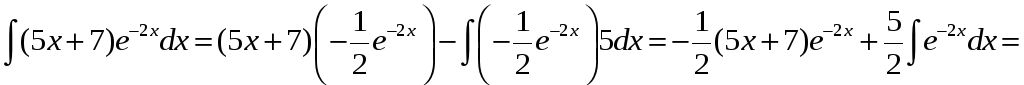
![]() +С.
+С.
Мы не будем проводить дальнейшее алгебраическое упрощение данного выражения.
Задача. Найти
![]() .
.
Пусть
![]() .
.
Тогда
![]() .
.
Применяя формулу интегрирования по частям, получаем
![]() .
.
Мы получили интеграл подобного типа, только степень многочлена стала меньше. Применим еще раз метод интегрирования по частям.
Пусть
![]() .
.
Тогда
![]() .
.
Получаем
![]() =
=
=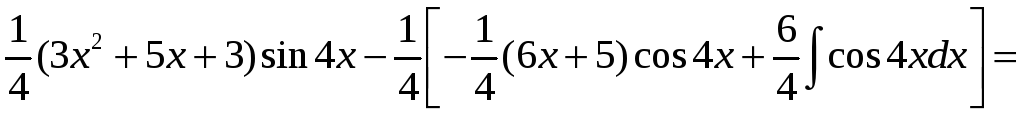
=![]()
Ответ:
![]()
![]()
Если вы хорошо
овладели навыками интегрирования, то
можно явно не выписывать чему равно
![]() и
и
![]() ,
,
![]() и
и
![]() ,
проделывая промежуточные выкладки в
уме. Покажем это на примере.
,
проделывая промежуточные выкладки в
уме. Покажем это на примере.
Задача. Найти![]() .
.

=![]() .
.
Ответ:
![]() =
=![]() .
.
Следующий тип интегралов, для которых применяется формула интегрирования по частям – это интегралы вида
![]() ,
где
,
где
![]() - многочлен степени
- многочлен степени
![]() ,
,
![]() целое положительное число. В этом случае
принимается
целое положительное число. В этом случае
принимается
![]() .
.
Задача. Найти
![]() .
.
Пусть
![]() ,
значит
,
значит
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Получаем
![]() =
=![]()
=![]()
Теперь обозначим
![]() ,
значит
,
значит
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Получаем
![]() =
=![]() =
=
=
=![]()
=![]() .
.
Ответ:
![]() =
=![]() .
.
Существует еще один класс интегралов, при вычислении которых полезно применить формулу интегрирования по частям. Применяемый прием называется «интегрирование с возвратом». Суть его состоит в том, что в результате применения формулы интегрирования по частям мы получаем уравнение для нахождения искомого интеграла.
Приведем пример
вычисления интегралов
вида
![]() и
и
![]() .
.
Задача. Найти
![]() .
.
Пусть
![]() .
Значит
.
Значит
![]() .
Тогда
.
Тогда
![]() .
.
Получаем
![]() .
.
Далее обозначим
![]() .
Значит
.
Значит
![]() .
Тогда, как и ранее
.
Тогда, как и ранее
![]() .
Применяя еще раз формулу интегрирования
по частям, получаем
.
Применяя еще раз формулу интегрирования
по частям, получаем
![]() =
=

Раскрываем скобки
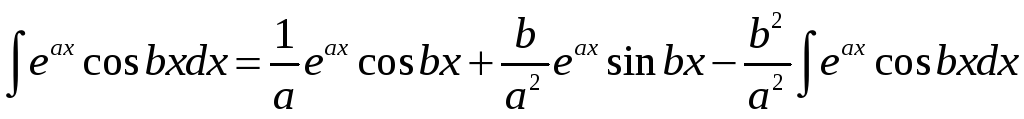 .
.
Фактически мы
получили уравнение для определения
искомого интеграла
![]() .
.
Переносим интеграл из правой части соотношения в левую
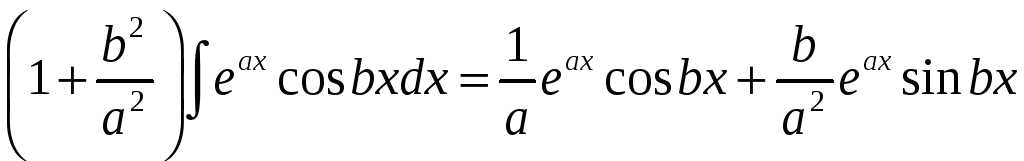 .
.
Получаем
![]() =
=![]() .
.
Задача. Найти
![]() .
.
Пусть
![]() .
Значит
.
Значит
![]() .
Тогда
.
Тогда
![]() .
.
Получаем
![]() .
.
Далее обозначим
![]() .
Значит
.
Значит
![]() .
Тогда, как и ранее
.
Тогда, как и ранее
![]() .
Применяя еще раз формулу интегрирования
по частям, получаем
.
Применяя еще раз формулу интегрирования
по частям, получаем
![]() =
=

Раскрываем скобки
![]() .
.
Переносим интеграл из правой части соотношения в левую
 .
.
Тогда
![]() =
=![]() .
.
Аналогичным образом могут быть вычислены интегралы вида:
![]() и
и
![]() .
.
Задача. Найти
![]() .
.
Обозначим
![]() ,
,
![]() .
Тогда
.
Тогда
 ,
,
![]() .
.
Применяя формулу интегрирования по частям, получаем
![]() =
= .
.
Преобразуем данное равенство к виду
![]() =
=
Последний из интегралов в правой части является табличным. Вычисляя его, имеем
![]() =
=![]()
Из полученного выражения следует
![]() =
=![]()
Тогда
![]() =
=![]() .
.
Задача. Найти
![]() .
.
Обозначим
![]() ,
,
![]() .
Тогда
.
Тогда
 ,
,
![]() .
.
Применяя формулу интегрирования по частям, получаем
![]() =
= .
.
Преобразуем данное равенство к виду
![]() =
=
=
Последний из интегралов в правой части является табличным. Вычисляя его, получаем
![]() =
=![]()
Из полученного выражения следует
![]() =
=![]()
Тогда
![]() =
= .
.
Интегрирование рациональных дробей.
Напомним, что рациональной дробью называется выражение вида:
 ,
где
,
где
![]() - многочлены степени
- многочлены степени
![]() и
и
![]() соответственно.
соответственно.
Дробь называется правильной, если степень многочлена в числителе строго меньше степени многочлена в знаменателе. В противном случае дробь называется неправильной.
Известно, что
всякая неправильная (![]() )дробь
может быть представлена в виде
)дробь
может быть представлена в виде
 =
=![]() ,
где
,
где
![]() - многочлен соответствующей степени, а
- многочлен соответствующей степени, а
![]() -
правильная рациональная дробь.
-
правильная рациональная дробь.
Поскольку проблема интегрирования многочлена не представляет серьезных трудностей, то основной вопрос – это интегрирование правильных рациональных дробей.
Простейшими рациональными дробями называются следующие выражения:
1)![]() ;
2)
;
2)
 ;
3)
;
3) ;
4)
;
4)
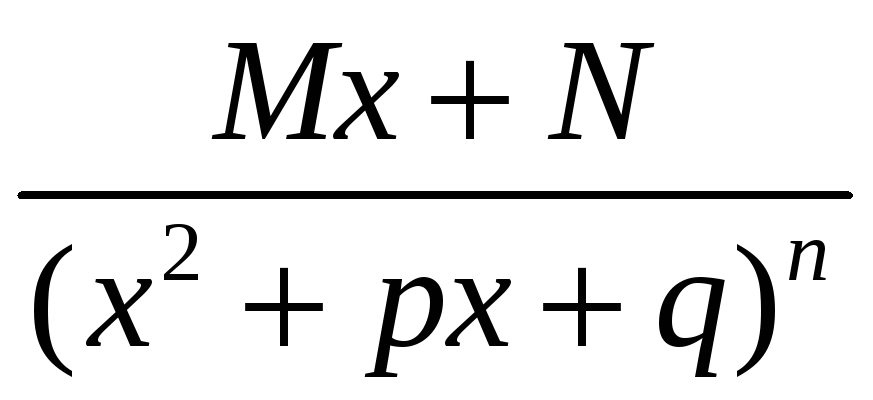 ,
,
где в последних
двух выражениях ![]() .
.
Известна теорема о том, что всякая правильная рациональная дробь может быть представлена в виде суммы простейших рациональных дробей.
Поясним вид такого представления.
Пусть имеется
правильная рациональная дробь
 .
.
Любой многочлен с действительными коэффициентами может быть представлен в виде произведения линейных и квадратных множителей.
Предположим, что
![]()
Где
![]() - целые числа,
- целые числа,
![]()
![]()
Тогда дробь
![]() может
быть представлена в виде
может
быть представлена в виде



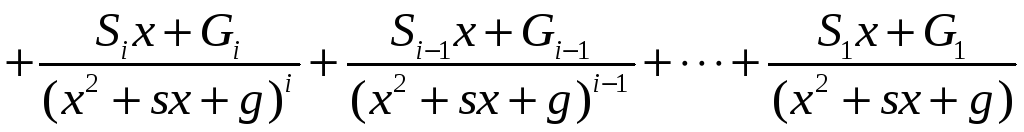 .
.
Методы определения коэффициентов разложения будут рассмотрены на конкретных примерах.
Приведем схему интегрирования простейших дробей.
1.
2.
3. Схема вычисления
интегралов вида
 была изложена
ранее.
была изложена
ранее.
4.Рассмотрим схему
вычисления интегралов вида
 .
.
Выделив полный квадрат, представим квадратный трехчлен в виде
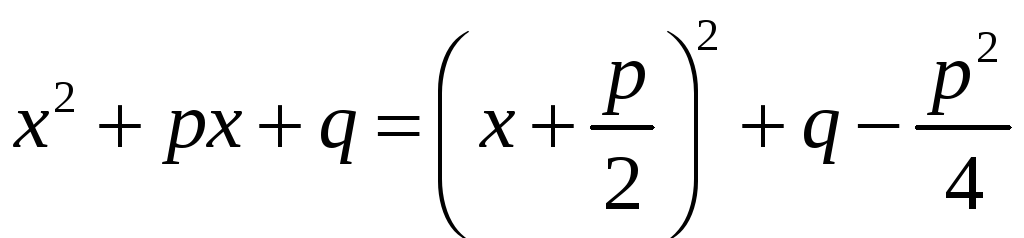 .
Поскольку
.
Поскольку
![]() ,
то обозначим
,
то обозначим
![]() .
Сделаем замену переменной
.
Сделаем замену переменной
![]() .
.
Тогда имеем
 .
.
Вычислим каждый интеграл отдельно.

Рассмотрим схему
вычисления второго интеграла
 .
Обозначим
.
Обозначим
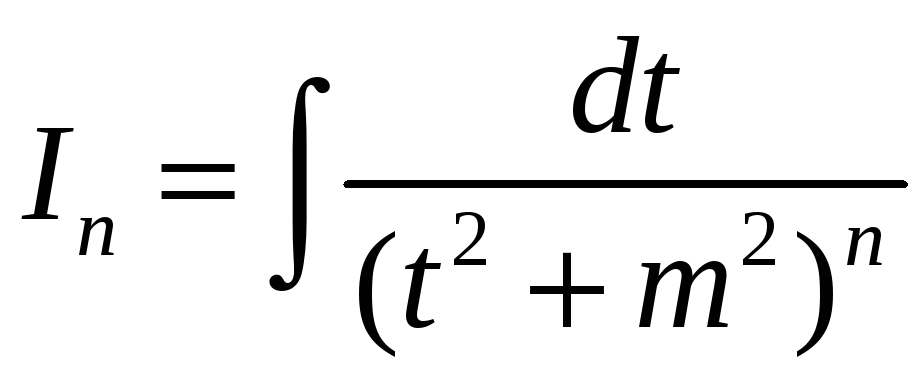 .
Его вычисление при
.
Его вычисление при
![]() не
представляет трудностей, поскольку он
является табличным интегралом
не
представляет трудностей, поскольку он
является табличным интегралом
 .
.
Далее наш метод
состоит в том, чтобы получить рекуррентное
соотношение, которое позволяет сводить
вычисление
 к вычислению
к вычислению
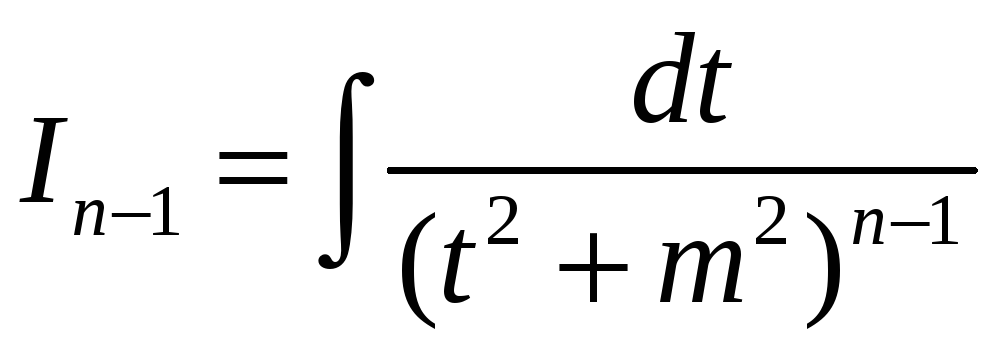 .
.
Преобразуем интеграл к виду

Это соотношение перепишем в виде

Для вычисления интеграла в правой части используем формулу интегрирования по частям. Обозначим:
![]() ,
,
 .
Тогда
.
Тогда
![]() ,
,
 .
.
Получаем
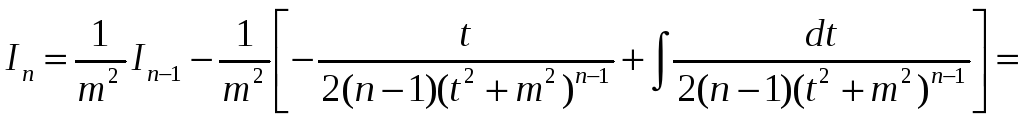
![]()
Таким образом
 .
.
Задача. Найти .
.
Используя полученное рекуррентное соотношение, получаем
 =
= .
.
Используем еще один раз рекуррентное соотношение.
Тогда
 =
=
Вычисление последнего интеграла не представляет трудностей. Следовательно
 =
=
Далее приведем примеры интегрирования рациональных дробей.
Задача. Найти

Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
 .
.
Осталось определить неизвестные пока коэффициенты А, В, С.
Приведем правую
часть к общему знаменателю, который
равен
![]() - знаменателю в левой части выражения
и приравняем числители в правой и левой
частях. Получим
- знаменателю в левой части выражения
и приравняем числители в правой и левой
частях. Получим
![]() .
(1)
.
(1)
В соотношении (1)
приравниваем коэффициенты при одинаковых
степенях
![]() и получаем систему уравнений для
определения А, В, С.
и получаем систему уравнений для
определения А, В, С.
 .
.
Решая эту систему
уравнений, находим коэффициенты. Отметим,
что в данном случае нет необходимости
решать систему уравнений, поскольку
неизвестные коэффициенты можно определить
более простым
путем.
Равенство (1) рассматриваем как равенство
многочленов, верное для любых значений
![]() .
Подставим в левую и правую части этого
равенства
.
Подставим в левую и правую части этого
равенства
![]() .
Получим
.
Получим
![]() ,
,
![]() .
.
Подставляя
![]() ,
имеем
,
имеем
![]() ,
,
![]() .
.
Подстановка
![]() дает
дает
![]() ,
,
![]() .
.
Следовательно
 .
.
Тогда
 =
=
= .
.
Ответ:
 =
=![]()
Задача. Найти

Поскольку дробь правильная, то представим ее в виде суммы простейших дробей вида
 .
.
Приводя к общему знаменателю, и, приравнивая числители в левой и правой частях, получаем
![]() .
(2)
.
(2)
Приравниваем
коэффициенты при одинаковых степенях
![]() и получаем систему уравнений для
определения А, В, С.
и получаем систему уравнений для
определения А, В, С.
 .
.
Решая эту систему
уравнений, находим коэффициенты. Отметим,
что в данном случае нет необходимости
полностью решать систему уравнений,
поскольку часть неизвестных коэффициентов
можно определить более простым путем.
Равенство (2) рассматриваем как равенство
многочленов, верное для любых значений
![]() .
Подставим в левую и правую части этого
равенства
.
Подставим в левую и правую части этого
равенства
![]() .
Получим
.
Получим
![]() ,
,
![]() .
.
Подставим в левую
и правую части этого равенства
![]() .
Получим
.
Получим
![]() ,
,
![]() .
.
Из первого уравнения системы находим
![]() .
.
Тогда
 .
.
Следовательно
 =
=
=
Ответ:
 =
=![]() .
.
Задача. Найти

Разложим это выражение на простейшие дроби
 .
.
Определяем коэффициенты
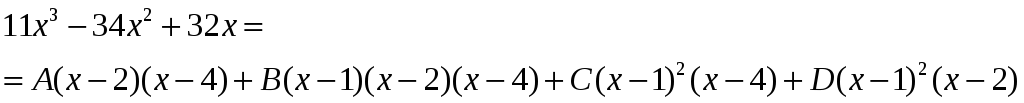
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
получаем
,
получаем

Часть коэффициентов определим независимым путем.
Полагая
![]() ,
,![]() ,
,
![]() получаем
получаем
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Тогда
![]() .
.
Следовательно
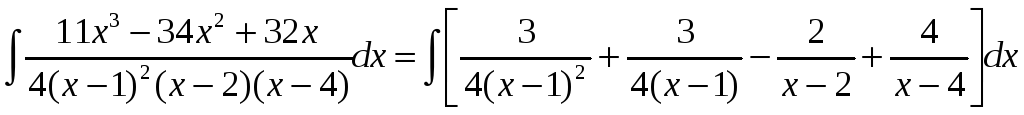 =
=
=

Ответ:


Задача. Найти
 .
.
Подынтегральное выражение является неправильной рациональной дробью. Представим его в виде суммы многочлена и правильной рациональной дроби.
Для этого используем схему деления многочлена на многочлен
-
_



 +1
+1_

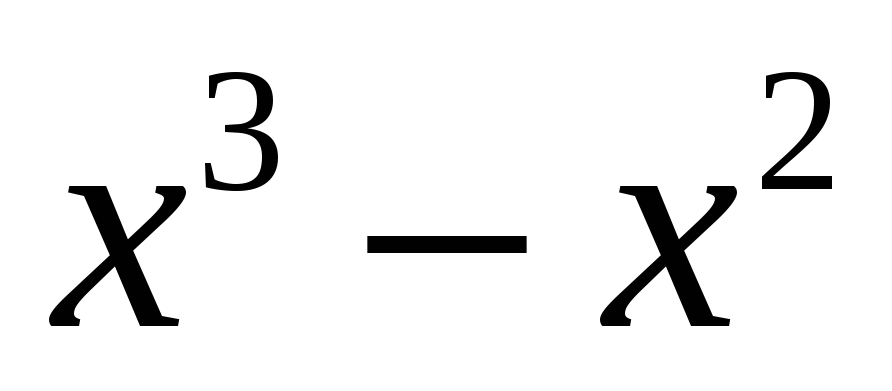

Следовательно
 =
=
Полученную
правильную рациональную дробь
 представим в виде суммы простейших
дробей
представим в виде суммы простейших
дробей
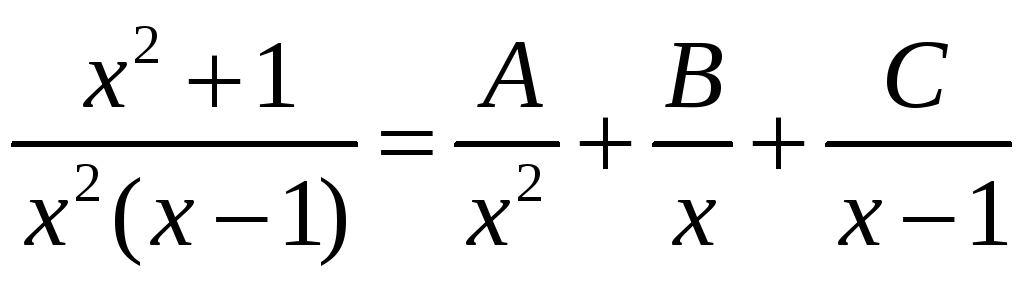
Приводя к общему знаменателю, и, приравнивая числители в левой и правой частях, получаем
![]()
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
имеем систему уравнений
,
имеем систему уравнений
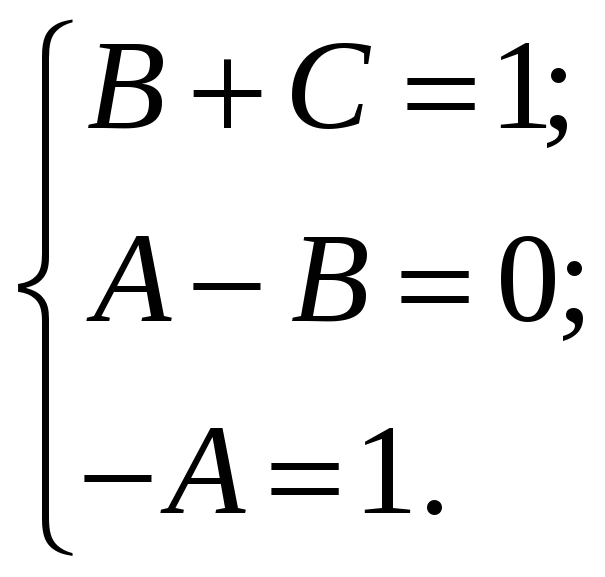
Решением этой
системы являются:
![]()
![]() ;
С=2.
;
С=2.
Тогда
 =
=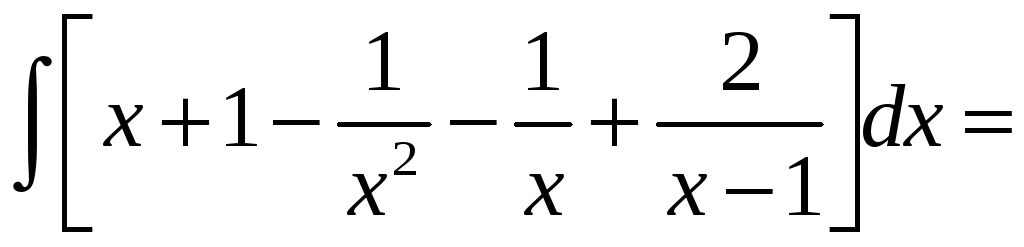
= .
.
Ответ:
 =
=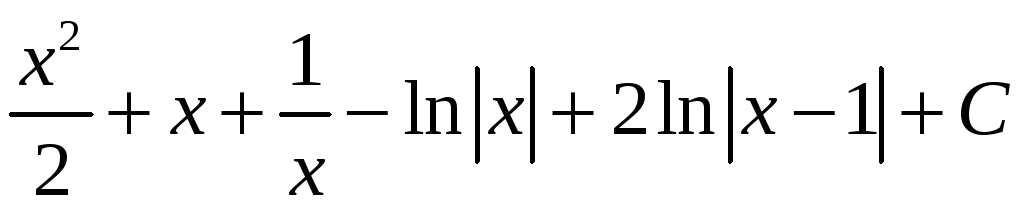 .
.
Задача. Найти
 .
.
Правильную
рациональную дробь
 представим в виде суммы простейших
дробей
представим в виде суммы простейших
дробей

Приводя к общему знаменателю, и, приравнивая числители в левой и правой частях, получаем
![]()
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
получаем систему уравнений
,
получаем систему уравнений

Коэффициент А
можно найти непосредственно подстановкой
![]() в исходное уравнение. Получаем
в исходное уравнение. Получаем
![]() ,
то есть
,
то есть
![]() .
.
Тогда
![]()
 =
= =
=
= =
=
 =
=
= =
=
= =
=
= .
.
Ответ:
![]()
 .
.
Интегралы, сводящиеся к интегрированию рациональных дробей.
Рациональной
функцией
![]() будем называть функцию, при вычислении
которой используются следующие
математические операции: сложение,
вычитание, умножение, деление, возведение
в целую степень.
будем называть функцию, при вычислении
которой используются следующие
математические операции: сложение,
вычитание, умножение, деление, возведение
в целую степень.
Интегралы
вида
![]() .
.
Данный интеграл
сводится к интегрированию рациональных
дробей заменой переменной
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
После подстановки получаем
![]() .
.
Полученное выражение является рациональной дробью.
Задача. Найти
![]()
Сделаем замену
переменной
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
После подстановки
получаем

Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
 .
.
Осталось определить неизвестные пока коэффициенты А, В, С.
Приведем правую
часть к общему знаменателю, который
равен
![]() - знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
- знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
![]() .
.
В полученном
соотношении приравниваем коэффициенты
при одинаковых степенях
![]() и получаем систему уравнений для
определения А, В, С.
и получаем систему уравнений для
определения А, В, С.
 .
.
Решая эту систему уравнений, находим коэффициенты.
![]() .
.
Тогда
 =
=
Подставляя
![]() ,
получаем
,
получаем
![]() =
=
Найти![]()
Сделаем замену
переменной
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
После подстановки получаем

Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
 .
.
Осталось определить неизвестные пока коэффициенты А, В, С.
Приведем правую
часть к общему знаменателю, который
равен
![]() - знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
- знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
![]() .
.
В полученном
соотношении приравниваем коэффициенты
при одинаковых степенях
![]() и получаем систему уравнений для
определения А, В, С.
и получаем систему уравнений для
определения А, В, С.
 .
.
Решая эту систему уравнений, находим коэффициенты.
![]() .
.
Тогда
 =
=
=
=![]()
=
=![]()
Подставляя
![]() ,
получаем
,
получаем
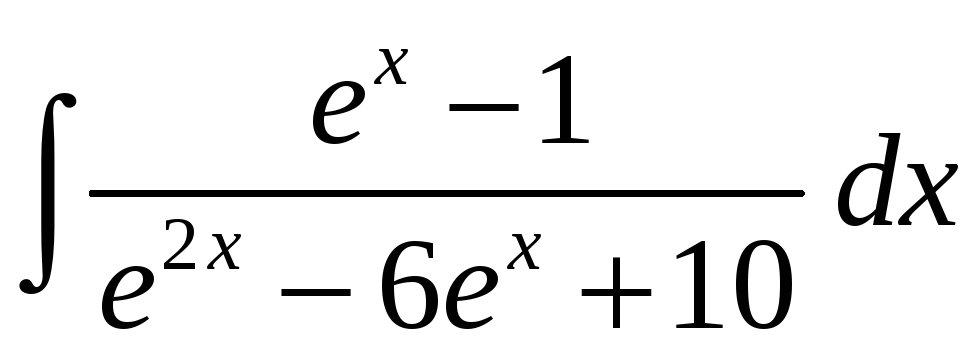 =
=![]() .
.
Задача. Найти
![]()
Сделаем замену
переменной
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
После подстановки
получаем
![]()
Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
![]() =.
=.
Осталось определить неизвестные пока коэффициенты А, В, С.
Приведем правую
часть к общему знаменателю, который
равен
![]() - знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
- знаменателю в левой части выражения,
и приравняем числители в правой и левой
частях. Получим
![]() .
.
В полученном
соотношении приравниваем коэффициенты
при одинаковых степенях
![]() и получаем систему уравнений для
определения А, В, С.
и получаем систему уравнений для
определения А, В, С.
 .
.
Решая эту систему уравнений, находим коэффициенты.
![]() .
.
Тогда
![]() .
.
Подставляя
![]() ,
получаем
,
получаем
![]() =
=![]() .
.
Интегралы вида
![]() .
.
Данный неопределенный интеграл сводится к интегрированию рациональной дроби по следующей схеме.
Обозначим через
![]() - наименьшее общее кратное чисел
- наименьшее общее кратное чисел
![]() .
(На всякий случай напомним, что наименьшим
общим кратным для некоторого множества
целых чисел называется такое наименьшее
целое число, которое делится без остатка
на все числа данного множества.)
.
(На всякий случай напомним, что наименьшим
общим кратным для некоторого множества
целых чисел называется такое наименьшее
целое число, которое делится без остатка
на все числа данного множества.)
Сделаем замену
переменной
![]() .
Тогда
.
Тогда
![]() .
.
После указанной замены подынтегральное выражение превращается в рациональную дробь.
Рассмотрим примеры.
Задача. Найти
![]() .
.
Подынтегральная
функция содержит
![]() и
и
![]() .
.
Наименьшим целым числом, которое делится на 2 и на 3 является число 6.
Сделаем замену
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Напомним, что
.
Напомним, что
![]() .
Следовательно
.
Следовательно
![]() ,
,
![]() .
.
Тогда
![]() .
.
Выражение, стоящее под знаком интеграла является неправильной рациональной дробью. Следовательно, его можно представить как сумму многочлена и правильной рациональной дроби.
Имеем
![]()
Следовательно
![]()
![]()
Подставляя
![]() ,
получаем
,
получаем
![]() =
=![]() .
.
Задача. Найти![]()
Сделаем замену
переменной
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
Тогда получаем
.
Тогда получаем
 .
.
Подставляя
![]() ,
получаем окончательный ответ
,
получаем окончательный ответ
![]() .
.
Интегралы вида
![]() .
.
Данный
интеграл сводится к интегрированию
рациональных дробей путем следующей
замены (так называемая «универсальная
тригонометрическая подстановка»).
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Из школьного курса тригонометрии известны формулы выражения синуса и косинуса через тангенс половинного угла. На всякий случай мы напомним эти формулы. Итак:
 .
.
 .
.
Такая подстановка приводит вычисление исходного интеграла к интегрированию рациональной дроби.
Задача. Найти
![]() .
.
Сделаем замену
переменной
![]() .
Тогда
.
Тогда

= .
.
Таким образом:
![]() =
= .
.
Задача. Найти
![]() .
.
Используя замену
![]() ,
получаем
,
получаем
 .
.
То есть
![]() .
.
Рассмотрим еще
один класс интегралов – интегралы
вида
![]() .
.
Поскольку
![]() ,
то данный тип интегралов можно вычислять,
используя универсальную тригонометрическую
подстановку. Однако существует замена
переменной, которая позволяет вычислить
этот интеграл более просто. Такой заменой
является
,
то данный тип интегралов можно вычислять,
используя универсальную тригонометрическую
подстановку. Однако существует замена
переменной, которая позволяет вычислить
этот интеграл более просто. Такой заменой
является
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
После такой подстановки вычисление
интеграла сводится к интегрированию
рациональной дроби.
.
После такой подстановки вычисление
интеграла сводится к интегрированию
рациональной дроби.
Задача. Найти
![]() .
.
Сначала убедимся, что данный интеграл действительно относится к указанному типу. Для этого преобразуем данное выражение
 .
.
Выражение
![]() является правильной рациональной дробью
и может быть разложено в сумму простейших
рациональных дробей. Имеем
является правильной рациональной дробью
и может быть разложено в сумму простейших
рациональных дробей. Имеем
![]()
После приведения к общему знаменателю в правой и левой частях получаем
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
получаем систему уравнений
,
получаем систему уравнений

Решая эту систему, получаем
![]() .
.
Следовательно
![]()
=![]()
=![]()
=![]() .
.
Получаем
![]() =
=![]() .
.
Задача. Найти![]()
После замены
переменной
![]() получаем
получаем
![]()
=![]() .
.
Следовательно
![]() =
=![]() .
.
Тригонометрические
подстановки в интегралах, содержащих
выражения
![]() ,
,
![]() ,
,
![]() .
.
В этих случая полезны следующие подстановки.
Для случая выражения
![]() используется
замена
используется
замена
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Для случая выражения
![]() используется
замена
используется
замена
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Для случая выражения
![]() используется
замена
используется
замена
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Задача. Найти
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Следовательно
![]()
=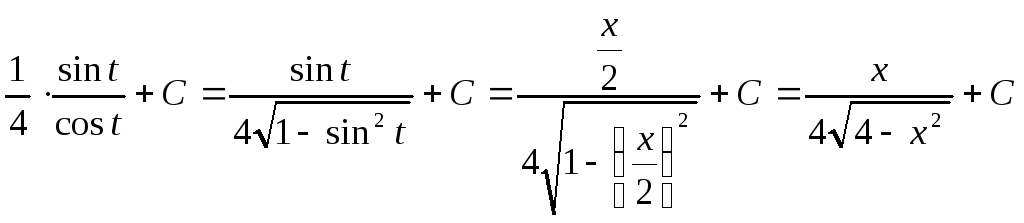 .
.
Получаем
![]() =
=![]() .
.
Задача. Найти
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Следовательно

= .
.
Получаем
![]()
![]() .
.
Найти
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]() ,
,
 .
.
Следовательно

= .
.
Получаем
![]()
![]() .
.
Интегралы вида
![]() .
.
Напомним некоторые формулы тригонометрии:
![]() ;
;
![]() ;
;
![]() .
.
Задача. Найти
![]() .
.
Решение.
![]()
=![]() .
.
Задача. Найти
![]() .
.
Решение.
![]()
![]()
=![]() .
.
Задача. Найти
![]() .
.
Решение.
![]()
![]()
=![]() .
.
Интегралы вида
![]() .
.
Рассмотрим два случая вычисления таких интегралов.
Первый случай
– это когда, по крайней мере, один из
показателей степени
![]() или
или
![]() является
нечетным числом. Будем считать для
определенности
является
нечетным числом. Будем считать для
определенности
![]() нечетным числом, то есть
нечетным числом, то есть
![]() .
Обозначим
.
Обозначим
![]() .
Следовательно
.
Следовательно
![]() .
.
Тогда
![]()
=![]() .
.
Полученное подынтегральное выражение является многочленом и его интегрирование не вызовет затруднений.
Задача. Найти
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Имеем
![]()
=![]()
![]() .
.
Задача. Найти
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Имеем
![]()
= .
.
Второй случай
– оба показателя степени
![]() и
и
![]() являются
четными числами.
являются
четными числами.
В этом случае для понижения степени используются формулы
![]() ;
;
![]() .
.
Задача. Найти
![]() .
.
Решение.
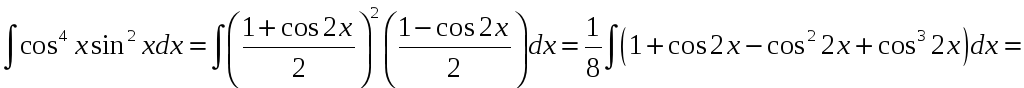
=![]()
=![]()
=![]()
=![]()
=![]() .
.
Таким образом
![]() =
=![]() .
.
Замечания:
- при вычислении
![]() мы воспользовались формулой двойного
угла
мы воспользовались формулой двойного
угла
![]() ;
;
- при вычислении
![]() мы воспользовались правилом интегрирования
в случае, когда, по крайне мере, одна из
степеней нечетная.
мы воспользовались правилом интегрирования
в случае, когда, по крайне мере, одна из
степеней нечетная.
Задача. Найти
![]() .
.
Решение.
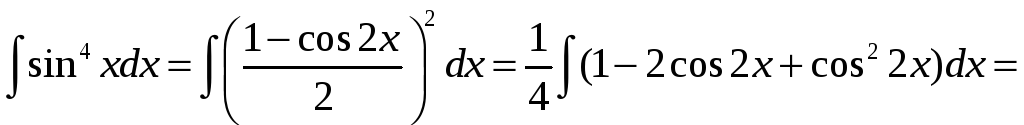
=![]()
=![]()
=![]() .
.
Получаем
![]() =
=![]() .
.
