1.3. Кратные и дольные единицы измерения.

Десятичные кратные и дольные единицы измерения и их наименования образуются с помощью множителей и приставок. Укажем приставки, их значения и обозначения, допускаемые ГОСТ (таблица 1.2).

Кратные и дольные единицы находят применение при решении практических задач для более удобного и компактного написания значений физических величин. При этом ГОСТ запрещает использовать двойные приставки, а также прибавлять приставки к единице измерения, которая сама является кратной величиной какой-либо другой единицы (даже тогда, когда название последней приставки не содержит, например, тонна). Так, нельзя употреблять название мегатонна; правильное употребление – тераграмм. Если единица измерения образована как произведение (или отношение) единиц, приставку необходимо присоединить к наименованию первой единицы: килоньютон-метр (кН·м), но не ньтон-километр (Н·км).

Однако для широко распространенных единиц измерения имеются исключения, например, тонна-километр (т·км), ватт на квадратный сантиметр (Вт/см²) и др. Надо также подчеркнуть, что выражение метр в квадрате (в кубе) – неверно. Следует писать (и говорить): квадратный (кубический) метр.

63

затухающих колебаний не будут определяться начальными условиями.

Они зависят от частоты ωв.

Для нахождения А_в и φ_в нужно найти х’ и х” из (6.31) и

подставить их, а также само уравнение (6.31) в (6.30). Расчеты дают

(6.32)

(6.32)

Анализ (6.32) приводит к следующим выводам:

a) пpи ωв = 0

б) при ;

в) при амплитуда А_в стремится к максимуму:

(см. рис. 6.5.).

6.5.2. Резонанс

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешнего гармонического воздействияω_в к собственной частоте системы называется резонансом. Частота ω_р, соответствующая резонансу, есть резонансная частота. Для её определения необходимо найти экстремум функции (6.32), т.е. продифференцировать подкоренное выражение в (6.32) и результат приравнять к нулю:

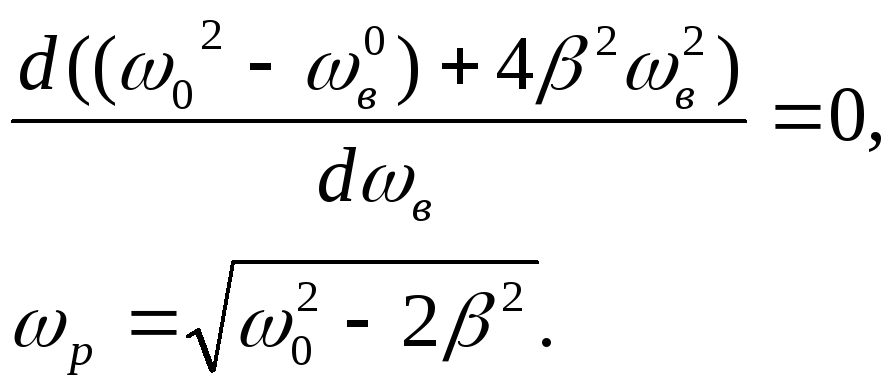(6.33)

Резонансные кривые показаны на рис. 6.5, на котором видно, что с увеличением коэффициента затухания, амплитуда, соответствующая резонансу, уменьшается. Также уменьшается и резонансная частота.

62

Рис. 6.4.

6.5. Вынужденные колебания

6.5.1. Дифференциальное уравнение вынужденных колебаний

Вынужденные колебания возникают при действии на систему внешней периодически изменяющейся (вынуждающей) силы

, (6.29)

где - циклическая частота вынуждающей силы, аF_m - её амплитуда.

Наряду с F_в на систему действуют квазиупругая сила F_y и сила сопротивления F_c. Уравнение движения в данном случае имеет вид:

, ,

. (6.30)

Решением этого дифференциального уравнения вынужденных колебаний является

, (6.31) где А_ви φ_в – соответственно амплитуда и начальная фаза вынужденных колебаний , которые в отличие от собственных незатухающих и

11

Таблица1.2

Множитель Приставка Множитель Приставка

наимено- обозна- наимено- обозна-

___________ вание чение вание чение

10¹⁸ экса Э 10^-1 деци д

10¹⁵ пэта П 10^-2 санти с

10¹² тэра Т 10^-3 милли м

10⁹ гига Г 10^-6 микро мк

10⁶ мега М 10^-9 нано н

10³ кило к 10^-12 пико п

10² гекто г 10^-15 фемто ф

10^-18 атто а_