
- •Федеральное агентство по образованию
- •6. Механические колебания. 56
- •1. Физические величины и их единицы измерения. Математические операции с физическими величинами. 6
- •2. Кинематика поступательного и вращательного
- •3. Динамика поступательного и вращательного
- •4. Силовые поля, закон всемирного тяготения.
- •5. Работа силы. Мощность. Энергия. 47
- •Физические основы механики
- •1.1. Элементы кинематики.
- •1.2. Динамика поступательного и вращательного движения.
- •1.3. Силовые поля. Элементы теории гравитационного поля.
- •§ 55 – 58; С 187 – 195;
- •§ 5.4 – 5.6; С. 55 – 62.
- •1.4. Работа силы. Мощность. Энергия.
- •1.5. Механические колебания.
- •1.1. Основные определения.
- •1.2. Международная (интернациональная) система единиц измерения физических величин (си).
- •6.6.2. Биения
- •6.6.3. Сложение двух взаимно перпендикулярных колебаний одинаковой частоты
- •6,5.3. Добротность
- •6.6. Сложение колебаний
- •6.6.1. Сложение двух гармонических колебаний одного направления и одинаковой частоты
- •1.3. Кратные и дольные единицы измерения.
- •6.5.2. Резонанс
- •6.5. Вынужденные колебания
- •6.5.1. Дифференциальное уравнение вынужденных колебаний
- •1.4. Некоторые рекомендации по правильному
- •1.5. Математические операции с
- •6.4. Собственные затухающие колебания
- •6.3.4. Энергия собственных незатухающих колебаний.
- •1.6.1. Умножение векторной величины на скаляр.
- •1.6.2. Сложение двух векторных величин.
- •1.6.3. Вычитание векторных величин.
- •1.6.4. Разложение векторных величин
- •6.3.Свободные незатухающие колебания.
- •1.6.5. Скалярное произведение двух векторов r1 и r2 определяется как скаляр (число).
- •1.6.6. Векторное произведение двух
- •1.7. Дифференцирование и интегрирование физических величин.
- •1.7.1. Табличные формулы.
- •6.2. Кинематика колебательного движения
- •6.1. Основные понятия
- •1.7.2. Полный дифференциал.
- •1.7.3. Дифференцирование векторных физических величин.
- •1.7.4. Интегральные и дифференциальные физические
- •5.8. Энергия вращательного и плоского движений.
- •5.6. Закон сохранения полной энергии (закон Ломоносова).
- •5.7. Применение законов сохранения импульса и энергии. Соударения.
- •2.1. Основные понятия.
- •2.2 Кинематика материальной точки.
- •5.5. Закон сохранения механической энергии
- •5.4.1. Потенциальная энергия упруго деформированного тела.
- •5.4.2. Потенциальная энергия гравитационного притяжения двух тел
- •5.4. Потенциальная энергия
- •2.3. Кинематика абсолютно твердого тела
- •2.4. Механический (классический) принцип относительности.
- •4.5. Гравитационное поле.
- •3.3. Закон сохранения импульса
1.5. Механические колебания.
Кинематика колебательного движения. Свободные незатухающие колебания. Гармонический классический осциллятор. Маятники. Энергия незатухающих колебаний. Собственные затухающие колебания. Коэффициент затухания, логарифмический декремент затухания. Вынужденные колебания. Изменение амплитуды и фазы при вынужденных колебаниях. Резонанс. Добротность. Сложение колебаний.
(2) §§ 49 – 60, с. 181 – 215;
(3) §§ 27.1 – 28.3, с. 298 – 318.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Савельев И.В. Курс физики. – М.: Наука, 1989, Т. 1.
2. Савельев И.В. Курс физики. – М.: Наука. 1989,Т. 2.
3. Детлаф А.А., Яворский Б.М. Курс физики – М.: Высшая школа, 1989.
4. Беликов Б.С. Решение задач по физике. – М.: Высшая школа, 1986.
5. Чертов А.Г. Физические величины. – М.: Высшая школа, 1990.
6
1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ ИЗМЕРЕНИЯ.
МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ С ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ
1.1. Основные определения.
Физическая величина – характеристика одного из свойств физического объекта, явления, процесса (например, длина, масса, время и т. п.).
Размер – количественное содержание физической величины.
Значение физической величины – оценка размера физической величины в виде некоторого числа принятых для неё единиц.* Его получают в результате измерений или вычислений. Различают истинное и действительное значения физических величин.
Истинное значение – значение физической величины, которое идеальным образом отражало бы соответствующую физическую величину.** Действительное значение – значение физической величины, найденное экспериментальным путём и настолько близкое к истинному значению, что для данного конкретного случая может его заменить.
Единица измерения физической величины – физическая величина, которой по определению присвоено числовое значение, равное 1, и применяемая для количественного выражения физических величин.
Как и физические величины, их единицы измерения имеют наименования и обозначения (так, наименованием единицы измерения длины является метр, обозначение – м).
Размерность физической величины dim – выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях ( так, размерность: dim ℓ = L ( в данном случае все остальные символы – в нулевой степени) dim t = T, dim m = M, dim V = L · T ֿ¹, dim F = L · М · T ֿ², а их единицы измерения: [ℓ] = м; [t] = c; [m] = кг; [V] = м·сֿ¹ ; [F] = м·кг·сֿ² = Н).
________________________________________________________
* Юдин М. Ф., Селиванов М. Н. и др. Основные термины в области метрологии: Словарь-справочник. М., 1989.
** ГОСТ 16263 – 70 ГСИ. Метрология. Термины и определения. М., 1970.
67
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ МЕХАНИКИ
Кинетика поступательного и вращательного движений.
Уравнения поступательного движения
![]()

Уравнения вращательного движения
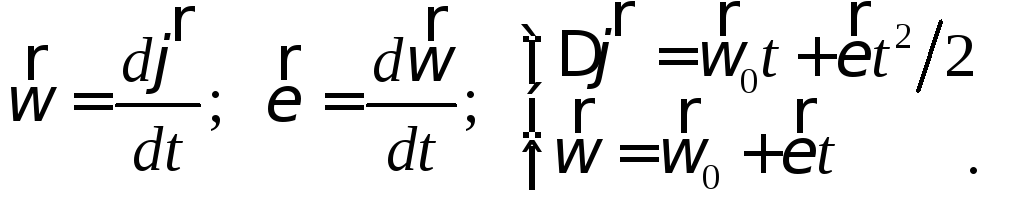
Нормальное
(центростремительное) ускорение
![]()
Тангенциальное
(касательное) ускорение
![]()
Взаимосвязь между угловыми и линейными скоростями и
ускорениями

Период
![]()
Угловая скорость:
![]()
Динамика поступательного движения
Импульс тела
![]() . Импульс силы
. Импульс силы![]()
Второй закон Ньютона

Третий закон
Ньютона
![]() .
.
Соотношения между импульсами силы и тела
![]()
Закон Всемирного
тяготения
![]()
Напряженность и потенциал гравитационного поля

66
Частные случаи:
а) когда разность
фаз
![]() ,
,![]() ,
,![]() ,
,![]() ,
..., то уравнение (6.39) сводится к уравнению
прямой:
,
..., то уравнение (6.39) сводится к уравнению
прямой:
![]() ;
;
б) когда
![]() …, то (6.39) принимает вид:
…, то (6.39) принимает вид:
![]() ,
что соответствует уравнению эллипса
с полуосями А1
и А2.
При А1=А2
, эллипс превращается в окружность.
,
что соответствует уравнению эллипса
с полуосями А1
и А2.
При А1=А2
, эллипс превращается в окружность.
7
