5.8. Энергия вращательного и плоского движений.

Кинетическая энергия вращательного движения

(сравните).

Кинетическая энергия плоского движения

(– скорость центра масс).

При этом .

54

Перемножим почленно каждое из равенств (5.22) и (5.23):

, .

Сложив их, получим:

.

Так как , a(см.(5.12)),

то ,

или .

Обобщим этот результат на случай нескольких взаимодействующих тел. Обозначив через и- суммарные кинетическую и потенциальную энергии, будем иметь: .Воспользовавшись правилом дифференцирования: ,придем к окончательному результату:

, (5.24)

где механическая энергия всех тел системы

Формула (5.24) является математическим выражением закона сохранения механической системы: механическая энергия консервативной системы остаётся постоянной.

Этот закон связан с однородностью времени, то есть с инвариантностью физических законов относительно выбора начала отсчета времени. Так, при свободном падении тела в гравитационном поле его скорость и перемещение зависят от начальной скорости и продолжительности падения, но не зависят от того, когда тело начало падать.

5.6. Закон сохранения полной энергии (закон Ломоносова).

Полной энергией будем называть не только сумму кинетической и потенциальной энергий, но и других видов энергии, например тепловую (трение, неупругая деформация и т.п.)

Словесная формулировка законы Ломоносова дана в п.5.2, аналитическая запись его похожа на формулу закона сохранения механической энергии (см.(5.24)): (5.24’)

5.7. Применение законов сохранения импульса и энергии. Соударения.

Соударение - это кратковременное столкновение тел. Прямая, проходящая через точку соприкосновения обоих тел называется линией дара. Если она проходит через центры масс то удар – центральный. Отношение

19

2. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ.

2.1. Основные понятия.

Механика – раздел физики, изучающий механические движения и происходящие взаимодействия материальных тел. В настоящее время различают три разновидности механики: классическую, релятивистскую и квантовую. В этом разделе мы будем рассматривать только классическую механику.

Под механическим движением понимают изменение с течением времени положения тел или их частей в пространстве. То есть, можно сказать, что движение происходит в пространстве и во времени.

Пространство и время – категории, обозначающие основные формы существования материи. Пространство выражает порядок существования отдельных объектов, время – порядок смены явлений.

В зависимости от вида реальных тел имеем механику: материальной точки, твёрдого тела и сплошной среды.

Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел (в условиях данной задачи). В дальнейшем материальную точку будем называть просто телом.

Под твёрдым телом понимается абсолютно твёрдое тело, деформациями которого пренебрегают в условиях данной задачи. Любое твёрдое тело можно представить как систему материальных точек.

К сплошной среде относятся жидкости, газы и другие деформируемые тела.

Механика подразделяется на кинематику, которая изучает движение тел без выяснения причин, их вызывающих, динамику, которая изучает законы движения взаимодействующих тел и статику, изучающую условия равновесия тел и являющуюся частным случаем динамики.

Кинематика оперирует следующими физическими величинами:

путь ∆ℓ, перемещение , скорость и ускорение движения (определения двух последних величин см. в п. 2.2).

Линия, описываемая в пространстве движущимся телом, называется траекторией. Расстояние между двумя точками, измеренное вдоль траектории, есть длина пути, или просто путь.

20

Вектор ∆, соединяющий две точки траектории (например, начальную и конечную), называется перемещением.

Система отсчета в механике – это совокупность системы координат и часов, связанных с некоторым телом, по отношению к которому определяется положение других тел в различные моменты времени. Системы отсчета подразделяются на инерциальные, покоящиеся или движущиеся равномерно и прямолинейно (то есть без ускорения) и неинерциальные, перемещающиеся с ускорением.

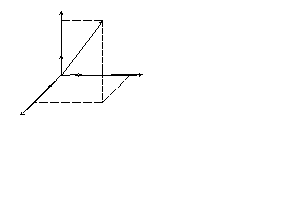
В физике обычно используют правую прямоугольную декартову систему координат (рис. 2.1). При этом положение точки в пространстве определяется радиусом-вектором или его проекциями на оси координат:r_x = x, r_y = y, r_z = z. Cам радиус-вектор, как известно из математики, может быть выражен через свои составляющие следующим образом:

= x·+y· + z· , (2.1) гдe ,,– орты, то есть единичные векторы.

z Кроме перечисленных понятий

необходимо знать такие, как явление,

z A свойство и физическая величина. Их

сущность раскрывается в следующих

примерах (см. также п. 1.1).

Инерция – явление сохранения

х состояния покоя или равномерного

0 прямолинейного движения.

у Рис. 2.1.

Инертность – свойство тел сохранять состояние покоя или равномерного прямолинейного движения. Масса – физическая величина, характеризующая инертность тела (см. также п. 3.1).