3.5. Численные методы нелинейного программирования

Среди наиболее известных и часто используемых на практике численных методов нелинейного программирования выделяют методы нулевого, первого и второго порядка. К методам нулевого порядка относят методы, реализация которых предполагает вычисление и использование только значений минимизируемой функции. В методах первого порядка помимо значений минимизируемой функции требуется вычисление ее производных первого порядка. Методы второго порядка предусматривают вычисление и использование значений минимизируемой функции, а также ее производных до второго порядка включительно. В соответствии с изложенным в предыдущих разделах, мы будем рассматривать численные методы нелинейного программирования применительно к решению задач вида

(3.5.1)

(здесь – множество простой структуры), а также применительно к решению задач безусловной минимизации

(3.5.2)

Методы нулевого порядка

Сеточный метод. Сеточный метод предусматривает дискретизацию допустимого множества задачи с помощью сетки, в узлах которой вычисляются значения целевой функции и среди них выбирается минимальное. Если целевая функция удовлетворяет условию Липшица, то его использование в ряде случаев помогает отбросить неперспективные области значений аргумента . Для функцииодной переменной условие Липшица имеет вид:

(3.5.3)

где – допустимое множество задачи (3.5.1) или задачи (3.5.2). Из (3.5.3) следует:

(3.5.4)

Это означает, что график целевой функции расположен над ломаной, уравнение которой определяется правой частью неравенства (3.5.4):

(3.5.5)

Если при некотором значении выполнено неравенство, то из дальнейшего рассмотрения исключается интервал значений аргумента, так как он является решением неравенства, гдеопределяется выражением (3.5.5).

Метод покоординатного спуска. Сначала рассмотрим этот метод применительно к решению задачи (3.5.2). Пусть – единичный координатный вектор, у которого-я координата равна, остальные равны нулю. Обозначим черезнекоторое начальное приближение и черезнекоторое положительное число, являющееся параметром метода. Допустим, что нам уже известны точкаи числопри каком-либо. Положим

(3.5.6)

где – целая часть числа. Соотношения (3.5.6) отражают циклический перебор координатных векторови, таким образом,и т.д. Вычислим значение функциив точкеи проверим неравенство

(3.5.7)

Если (3.5.7) выполняется, то примем

(3.5.8)

В том случае, если (3.5.7) не выполняется, вычисляем значение функции в точкеи проверяем неравенство

(3.5.9)

В случае выполнения (3.5.9) положим

(3.5.10)

Назовем -ю итерацию удачной, если справедливо хотя бы одно из неравенств (3.5.7) или (3.5.9). Если-я итерация неудачная, т.е. не выполняются оба неравенства (3.5.7) и (3.5.9), то полагаем

(3.5.11)

Здесь – фиксированное число, являющееся параметром метода. Условия (3.5.11) означают, что если за один цикл изитераций при переборе направлений всех координатных осейс шагомреализовалась хотя бы одна удачная итерация, то длина шагане дробится и сохраняется на протяжении по крайней мере следующего цикла изитераций. Если же среди последнихитераций не оказалось ни одной удачной итерации, то шагдробится. Таким образом, если на итерации с номеромпроизошло дробление, то

(3.5.12)

при всех .

Метод (3.5.6) – (3.5.11), как и другие методы нулевого порядка, не требует для своей реализации знания градиента минимизируемой функции. Однако если функция не является гладкой, то, как показано в [1], метод покоординатного спуска может не сходиться к множеству решений задачи (3.5.2). Проиллюстрируем это следующим примером.

Пример 3.5.1

Пусть в задаче (3.5.2)

Нетрудно проверить, что данная функция сильно выпукла наи, следовательно, достигает своего минимального значения нав единственной точке. Возьмем в качестве начального приближения точку. Тогда,

при всех действительных . Отсюда следует, что все итерации метода (3.5.6) – (3.5.11) при начальной точкеи любом выборе начального параметрабудут неудачными, т.е.при всехОднако в точкефункцияне достигает своего минимального значения на: например, приполучим.

Рассмотренный метод покоординатного спуска может быть модифицирован применительно к задаче (3.5.1). Пусть – допустимое множество этой задачи:

Предположим, что -е приближениеи числопри некоторомуже найдены. Выберем векторсогласно (3.5.6), сформируем точкуи проверим условия

(3.5.13)

Если оба условия (3.5.13) выполняются, то следующее приближение определяем по формулам (3.5.8). Если же хотя бы одно из условий (3.5.13) не выполнено, то формируем точкуи проверяем условия

(3.5.14)

В случае выполнения условий (3.5.14) следующее приближение находим по формулам (3.5.10), а если хотя бы одно из условий (3.5.14) не выполнено, то следующее приближение определяется из соотношений (3.5.11). В [1] показано, что если является -мерным параллелепипедом, а функция выпукла и непрерывно дифференцируема на, то при любом выборе начальныхипоследовательность, получаемая методом (3.5.13), (3.5.8), (3.5.14), (3.5.10), (3.5.11), минимизирует функциюнаи сходится к множеству решений экстремальной задачи.

Известны и другие варианты метода покоординатного спуска. Например, последовательность может быть построена по правилу

(3.5.15)

где определяется согласно (3.5.6), а– условиями

(3.5.16)

Метод (3.5.15), (3.5.16) имеет смысл применять тогда, когда величина из (3.5.16) может быть найдена в явном виде. Это будет иметь место, например, в случае, если целевая функция– квадратичная, т.е.

(3.5.17)

где – симметрическая положительно определенная матрица,. Для функции (3.5.17) метод (3.5.15), (3.5.16) приводит к методу Зейделя решения систем линейных уравнений.

Несмотря на то, что скорость сходимости метода покоординатного спуска в общем случае невысокая, благодаря простоте каждой итерации и не слишком жестким требованиям к гладкости минимизируемой функции этот метод весьма широко применяется на практике.

Метод случайного поиска. Метод случайного поиска характеризуется намеренным введением элемента случайности в алгоритм поиска. Во многих вариантах реализации метода последовательность строится по правилу:

(3.5.18)

где – некоторая положительная величина,– какая-либо реализация-мерной случайной величиныс известным законом распределения вероятностей. Например, координаты случайного векторамогут представлять собой независимые случайные величины, распределенные равномерно на отрезке. Очевидно, что компьютерная реализация данного метода требует использования датчика (или генератора) случайных чисел, имеющегося в стандартном программном обеспечении.

Рассмотрим несколько вариантов реализации метода случайного поиска минимума функции на множестве, предполагая, что-е приближениеуже известно.

Алгоритм с возвратом при неудачном шаге. С помощью датчика случайных чисел получают некоторую реализацию случайного вектора и в пространствеопределяют точку. Еслии, то сделанный шаг считается удачным, и в этом случае полагается. Если, но, или же, то сделанный шаг считается неудачным и полагается.

В том случае, если окажется, что для достаточно больших, то точкаможет быть принята в качестве приближения искомой точки минимума.

Алгоритм наилучшей пробы. Формируются какие-либо реализацийслучайного вектораи вычисляются значения целевой функциив тех точках, которые принадлежат множеству. Затем полагается, где индексопределяется условием

Здесь иявляются параметрами алгоритма.

Алгоритм статистического градиента. Генерируются реализацийслучайного вектораи вычисляются разностидля всех. Затем находят вектор, где сумма берется по всем тем, для которых. Если, то принимается. Если же, то повторяют описанный процесс с новым набором изреализаций случайного вектора. Величиныявляются параметрами алгоритма. Векторназывается статистическим градиентом. Еслии векторыявляются неслучайными и совпадают с соответствующими единичными векторами, то описанный алгоритм превращается в разностный аналог градиентного метода.

В рассмотренных вариантах метода случайного поиска закон распределения вероятностей случайного вектора предполагался не зависящим от номера итерации. Такой поиск называют случайным поиском без обучения. В алгоритмах, реализующих случайный поиск без обучения, отсутствуют анализ результатов выполненных итераций и определение перспективных направлений продолжения поиска точки минимума, в силу чего скорость сходимости в общем случае оказывается невысокой. Однако если на каждой очередной итерации учитывать накопленный опыт поиска минимума на предыдущих итерациях и перестраивать вероятностные свойства поиска так, чтобы направления, более перспективные в смысле убывания функции, становились более вероятными, то от метода случайного поиска можно ожидать большей эффективности. Таким образом, желательно иметь алгоритмы случайного поиска, обладающие способностью к самообучению и самоусовершенствованию в процессе поиска минимума в зависимости от конкретных особенностей минимизируемой функции. Такой поиск называют случайным поиском с обучением. Обучение осуществляется путем целенаправленного изменения закона распределения вероятностей случайного векторав зависимости от номера итерации и результатов предыдущих итераций таким образом, чтобы перспективные направления поиска сделать более вероятными, а другие направления – соответственно менее вероятными. Поскольку на различных этапах метода случайного поиска с обучением используются реализации случайных векторовс различными законами распределения вероятностей, итерационный процесс (3.5.18) удобнее записать в виде, учитывающем зависимость случайного вектораот:

(3.5.19)

В начале поиска закон распределения случайного вектора выбирают с учетом имеющейся априорной информации о минимизируемой функции. Если такая информация отсутствует, то поиск обычно начинают со случайного вектора, компоненты которого являются независимыми случайными величинами, распределенными равномерно на отрезке.

Для обучения алгоритма в процессе поиска часто используют семейство случайных векторов , зависящих от параметров, и при переходе от-й итерации к-й итерации имеющиеся значения параметровзаменяют новыми значениямис учетом результатов предыдущего поиска.

Рассмотрим два варианта метода случайного поиска с обучением для минимизации функции на всем пространстве.

Алгоритм покоординатного обучения. Пусть имеется семейство случайных векторов , каждая координатакоторых принимает два значения:с вероятностьюис вероятностью, где вероятностьзависит от параметраследующим образом:

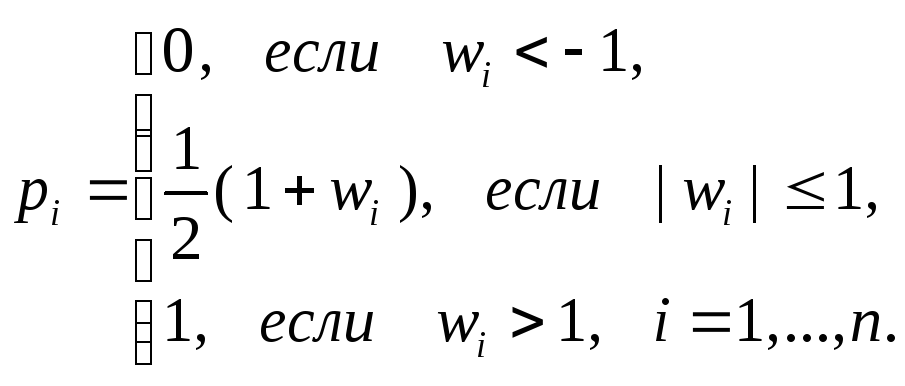(3.5.20)

Пусть начальное приближение уже выбрано. Тогда для определения следующего приближенияв формуле (3.5.19) прииспользуется какая-либо реализация случайного вектора, соответствующего набору значений параметров. Приближениеопределяется по формуле (3.5.19) прис помощью случайного вектора. Допустим, что известны приближенияи значения параметровпри некотором. Тогда полагаем

(3.5.21)

где величина называется параметром забывания,– параметром интенсивности обучения,. При определении следующего приближенияв формуле (3.5.19) используем реализацию случайного вектора.

Из (3.5.20), (3.5.21) видно, что если переход от точки кпривел к уменьшению значения функции, то вероятность выбора направленияна следующем шаге увеличивается. Если же при переходе откзначение функции увеличилось, то вероятность выбора направленияна последующем шаге уменьшается. Таким образом, посредством формул (3.5.21) осуществляется обучение алгоритма. Величинав (3.5.21) регулирует скорость обучения: чем больше, тем быстрее обучается алгоритм; приобучение отсутствует. Величинав (3.5.21) регулирует влияние предыдущих значений параметров на обучение алгоритма; приалгоритм «забывает» предыдущие значения. Для устранения возможного чрезмерного детерминирования алгоритма и сохранения его способности к достаточно быстрому обучению на параметрынакладываются ограниченияи при нарушении этих ограниченийзаменяются ближайшим из чисели,. Величиныявляются параметрами алгоритма.

Вместо формул (3.5.21) часто пользуются формулами

(3.5.22)

Рассмотренный алгоритм покоординатного обучения имеет недостаток, состоящий в том, что поиск и обучение происходят лишь по одному из направлений, где либо, либо. Отсутствие «промежуточных» направлений делает покоординатное обучение немобильным в областях с медленно изменяющимися направлениями спуска. От этого недостатка свободен следующий алгоритм.

Алгоритм непрерывного самообучения. Пусть имеется семейство случайных векторов , где– параметры обучения,– случайный вектор, координатыкоторого являются независимыми случайными величинами, распределенными равномерно на отрезке. Поиск начинается с рассмотрения случайных векторов, реализации которых используются при определении приближенийпо формулам (3.5.19). Обучение алгоритма припроизводится так же, как в алгоритме покоординатного обучения, с помощью формул (3.5.21) или (3.5.22). При больших значенияхвлияние случайной величиныуменьшается, и направлениестановится более детерминированным и близким к направлению. Во избежание излишней детерминированности метода на параметрынакладывают ограничения, и при нарушении этих ограниченийзаменяется на. Рассмотренный алгоритм, также как и алгоритм покоординатного обучения, характеризуется уменьшением фактора случайности и увеличением степени детерминированности в ходе поиска минимума, следуя преимущественно направлению убывания функции. В то же время наличие случайного фактора в выборе направления дает возможность придать алгоритму большую гибкость, особенно в тех случаях, когда свойства целевой функции в районе поиска изменились или предыдущее обучение оказалось недостаточно точным.