7. Задача:
Величина
момента импульса тела изменяется с
течением времени по закону
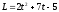 (в единицах СИ). Если в момент времени2
c
угловое ускорение составляет
(в единицах СИ). Если в момент времени2
c
угловое ускорение составляет
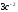 ,
то момент инерции тела (в кгм2)
равен …
,
то момент инерции тела (в кгм2)
равен …
Решение:
Скорость
изменения величины момента импульса
относительно неподвижной оси равна
величине суммарного момента внешних
сил относительно этой оси, то есть
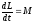 ,
гдеL
– величина момента импульса, M
–
величина момента силы.
,
гдеL
– величина момента импульса, M
–
величина момента силы.
Вычислив
производную от функции, характеризующей
зависимость величины момента импульса
от времени, получим величину момента
силы
 .
.
Используя
основной закон динамики вращательного
движения твердого тела вокруг неподвижной
оси, можем определить его момент инерции:
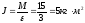 .
.
8. Задача:
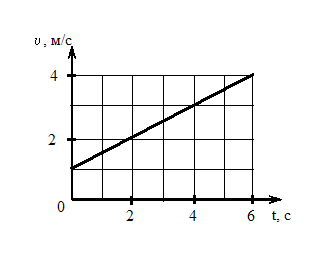
Твердое
тело вращается вокруг неподвижной оси.
Скорость точки, находящейся на расстоянии
10 см
от оси, изменяется со временем в
соответствии с графиком, представленным
на рисунке.
 Зависимость
угловой скорости тела от времени (в
единицах СИ) задается уравнением …
Зависимость
угловой скорости тела от времени (в
единицах СИ) задается уравнением …
Решение:
Связь
между модулями угловой скорости вращения
тела и линейной скоростью точки, отстоящей
от оси вращения на расстояние R,
имеет вид
 .
.
Отсюда
угловая скорость
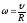 ,
причемR
= 10 см
=
0,1 м.
,
причемR
= 10 см
=
0,1 м.
Из
представленного графика начальная
скорость
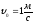 ,
ускорение
,
ускорение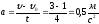 .
.
Тогда
зависимость скорости точки от времени
в единицах СИ задается уравнением
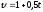 ,
а зависимость угловой скорости вращения
тела от времени – уравнением
,
а зависимость угловой скорости вращения
тела от времени – уравнением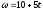 .
.
9. Задача:
На
барабан радиусом
 намотан шнур, к концу которого привязан
груз массой
намотан шнур, к концу которого привязан
груз массой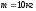 .
Груз опускается с ускорением
.
Груз опускается с ускорением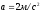 .
Момент инерции барабана …
.
Момент инерции барабана …
Решение:
Запишем
уравнение движения груза
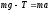 ,
гдеT
– сила натяжения шнура, под действием
которой также происходит вращение
барабана.
,
гдеT
– сила натяжения шнура, под действием
которой также происходит вращение
барабана.
Уравнение
вращения барабана
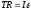 .
.
Ускорение
поступательного движения груза совпадает
с линейным ускорением точек на поверхности
барабана, поэтому ускорение груза a
и угловое ускорение барабана
связаны соотношением
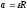 .
.
Из
этих уравнений найдем
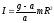 .
.
Подставляя
числовые значения, получим
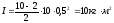 .
.
10. Задача:
Тело
массы
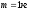 поднимают по наклонной плоскости. Высота
наклонной плоскости
поднимают по наклонной плоскости. Высота
наклонной плоскости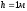 ,
длина ее основания
,
длина ее основания ,
коэффициент трения
,
коэффициент трения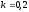 .
Минимальная работа, которую надо
совершить, вДж
равна …
.
Минимальная работа, которую надо
совершить, вДж
равна …
Решение:
Минимальная
сила, которую надо приложить к телу,
чтобы поднимать его по наклонной
плоскости без ускорения, равна сумме
составляющей силы тяжести, параллельной
наклонной плоскости, и силы трения:
 .
Работа равна
.
Работа равна ,
гдеl
– длина наклонной плоскости. Учитывая,
что
,
гдеl
– длина наклонной плоскости. Учитывая,
что
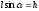 и
и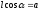 ,
получим
,
получим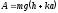 .
Следовательно, минимальная работаA
= 14 Дж.
.
Следовательно, минимальная работаA
= 14 Дж.
11. Задача:
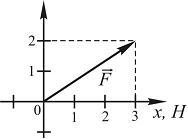
На рисунке показан вектор силы, действующей на частицу: Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), равна ______ Дж.
Решение:
По
определению
 .
С учетом того, что
.
С учетом того, что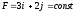 (см. рис.),
(см. рис.),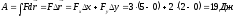
12. Задача
Амплитуда
затухающих колебаний уменьшилась в
![]() раз
(
раз
(![]() – основание натурального логарифма)
за
– основание натурального логарифма)
за
![]() .
Коэффициент затухания (в
.
Коэффициент затухания (в![]() )
равен …
)
равен …
Решение:
Амплитуда
затухающих колебаний изменяется со
временем по закону
![]() ,
где
,
где![]() –
коэффициент затухания. По условию
–
коэффициент затухания. По условию
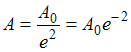 .
Тогда
.
Тогда![]() и
и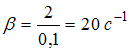 .
.
Ответ: 20 с-2
13. Задача:
Материальная
точка совершает гармонические колебания
по закону
 .
Период
колебания точки равен…
.
Период
колебания точки равен…
Решение:
Зависимость
координаты материальной точки от времени
при гармонических колебаниях определяется
выражением
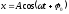 ,
гдеA
- амплитуда,
- круговая частота, 0
- начальная фаза колебаний. Период
колебаний равен
,
гдеA
- амплитуда,
- круговая частота, 0
- начальная фаза колебаний. Период
колебаний равен
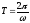 .
В данной задаче
.
В данной задаче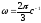 ,
следовательно, период
,
следовательно, период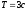 .
.
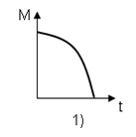
14. Задача
Величина
момента импульса тела относительно
неподвижной оси изменяется по закону![]() ;
при этом зависимость величины момента
сил, действующих на тело, описывается
графиком …
;
при этом зависимость величины момента
сил, действующих на тело, описывается
графиком …
Решение:
Скорость
изменения величины момента импульса
относительно какой-то неподвижной оси
равна величине суммарного момента
внешних сил относительно этой оси, т.е.
![]() где
где![]() –
величина момента импульса,
–
величина момента импульса,![]() –
величина момента силы.
Вычислив
производную от функции, характеризующей
зависимость величины момента импульса
от времени, получим зависимость величины
момента силы от времени.
–
величина момента силы.
Вычислив
производную от функции, характеризующей
зависимость величины момента импульса
от времени, получим зависимость величины
момента силы от времени.
![]() .
Графиком
этой функции является убывающая ветвь
параболы.
.
Графиком
этой функции является убывающая ветвь
параболы.