Лекции по физике / 3.2.Работа по перемещению заряда в эл.поле

§ 3.2. .Работа по перемещению заряда в электростатическом поле

На заряд со стороны электростатического поля действует сила. Поэтому при перемещении заряда в электростатическом поле совершается работа.

Силы электростатического поля являются консервативными, т.е. работа сил электростатического поля по перемещению заряда не зависит от формы пути, а определяется только положением начальной и конечной точек пути. Покажем это. Пусть точечный заряд +q₀ перемещается в поле неподвижного точечного заряда +q в вакууме из точки 1 в точку 2. Элементарная работа кулоновской силы, действующей на заряд со стороны заряда на пути dl равна dA = F•dl•cosα. По закону Кулона , dl•cosα = dr. Тогда 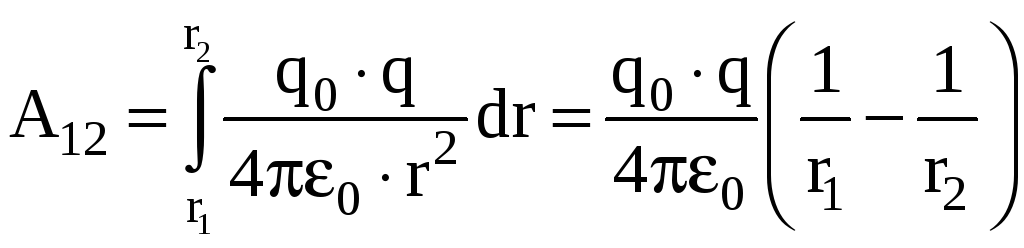. То есть работа определяется только положением точек 1 и 2.

В механике мы определили, что:

• консервативными называются силы, работа которых не зависит от формы пути, а определяется только координатой начального и конечного положения материальной точки;

• поле консервативных сил потенциально.

Для потенциальных полей можно ввести понятия потенциала и разности потенциалов. Обозначаются: потенциал φ, разность потенциалов φ₁-φ₂. Измеряются в СИ в вольтах (В).

Потенциал данной точки электростатического поля численно равен работе сил электростатического поля по перемещению единичного положительного заряда из данной точки поля в бесконечность.

Разность потенциалов φ₁-φ₂ между точками электростатического поля (1 и 2) численно равна работе, совершаемой силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2.

Ранее была получена формула для работы поля точечного заряда q по перемещению заряда q₀ из точки 1 в точку 2: 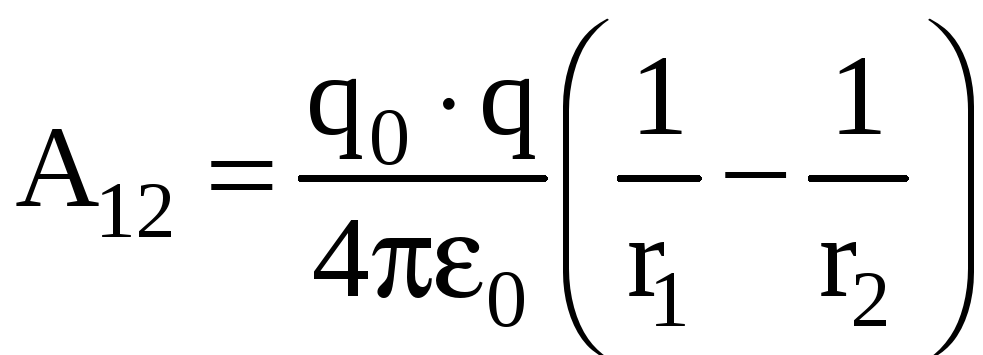. С другой стороны работа сил любого электростатического поля при перемещении заряда q₀ из точки 1 в точку 2 равна A₁₂ = q₀^.(φ₁-φ₂). Следовательно, 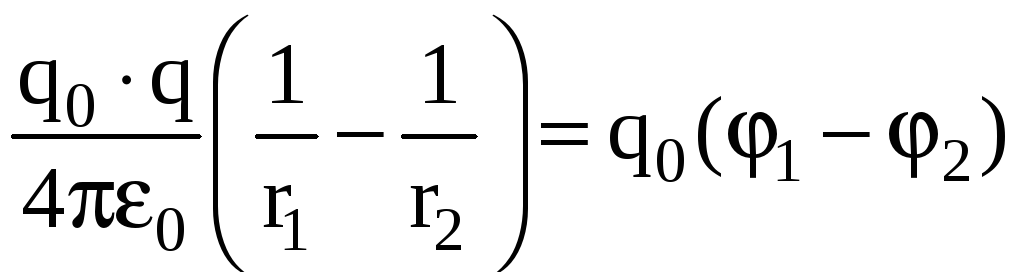. Отсюда находим выражение для потенциала электростатического поля точечного заряда q в вакууме: .

Принцип суперпозиции полей: потенциал электростатического поля, создаваемого системой зарядов равен алгебраической сумме потенциалов полей, создаваемых каждым из этих зарядов в отдельности _.

Потенциальная энергия заряда q₀ в точке электростатического поля с потенциалом φ: W_П = q₀^.φ. Это значит, что потенциал – энергетическая характеристика электростатического поля.

Электростатическое поле характеризуется двумя величинами: 1) напряженностью (силовая характеристика); 2) потенциалом (энергетическая характеристика). Можно предположить, что эти величины как-то связаны друг с другом. Покажем, что это так.

Работа сил поля по перемещению заряда q₀ на отрезке пути : , где - проекция вектора на направление перемещения . С другой стороны, эта работа будет равна убыли потенциальной энергии заряда: . Приравнивая правые части выражений для работы поля, получаем, что , отсюда , что означает: проекция вектора напряжённости электростатического поля на некоторое произвольное направление равна производной от потенциала по этому направлению с противоположным знаком. Здесь - быстрота изменения потенциала в данном направлении.

В силу произвольности выбора направления, можно записать , или: 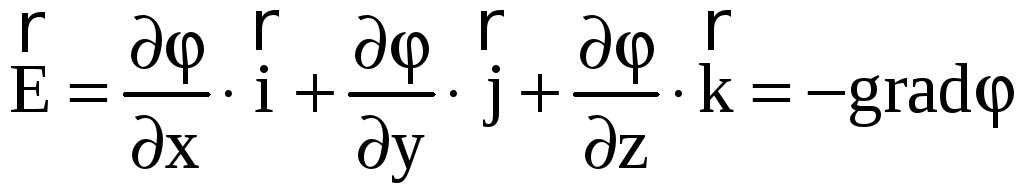. Эта формула выражает связь напряжённости электростатического поля с потенциалом: напряжённость электростатического поля равна градиенту потенциала, взятому с противоположным знаком. Знак минус означает, что напряжённость поля направлена в сторону убывания потенциала.

Таким образом, если известно значение потенциала φ в каждой точке поля, то можно найти напряжённость в каждой точке поля по формуле . Можно решить и обратную задачу, т.е. по заданным значениям в каждой точке найти разность потенциалов между двумя произвольными точками поля по формуле 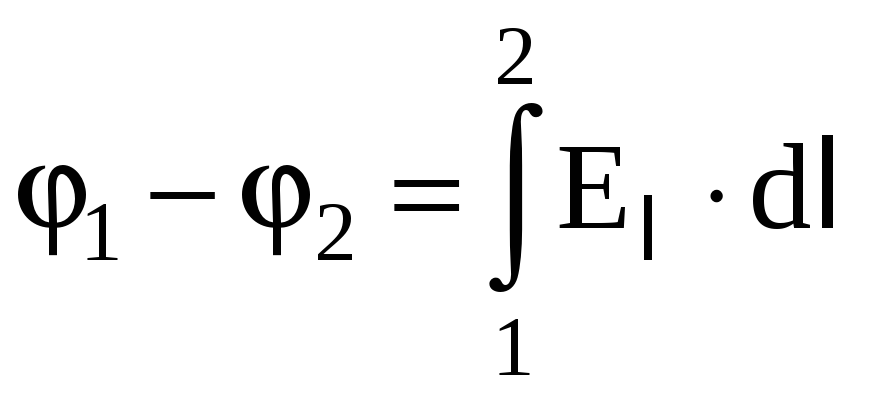. Интеграл можно брать по любой линии, соединяющей точки 1 и 2 (т.к. работа сил электростатического поля не зависит от формы пути).

Для однородного поля или , где d – расстояние между точками 1 и 2 вдоль силовой линии.

Для графического изображения электростатического поля также служат поверхности равного потенциала или эквипотенциальные поверхности.

Эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал.

Эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между соседними поверхностями была всюду одна и та же. Таким образом, чем гуще располагаются эквипотенциальные поверхности, тем больше в данном месте grad φ и, следовательно, больше напряжённость .

Силовые линии перпендикулярны эквипотенциальным поверхностям, т.к. работа перемещения заряда вдоль эквипотенциальной поверхности равна нулю, и, следовательно, сила, действующая на заряд перпендикулярна его перемещению.

Для однородного поля эквипотенциальные поверхности – это параллельные плоскости перпендикулярные силовым линиям поля.

4