Лекции по физике / 3.6.Явление электромагнитной индукции

§ 3.4 Явление электромагнитной индукции

В 1820 г. датский ученый Ханс Христиан Эрстед (1777 – 1851) показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Связь магнитного поля с током дала толчок к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальное открытие было блестяще сделано в 1831 г. английским физиком М. Фарадеем.

Опыт 1. Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (т.е. возникает электрический ток). При этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения электрического тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.

О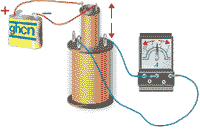пыт 2. Концы одной из катушек, которая вставлена одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. В моменты включения или выключения тока наблюдается отклонение стрелки гальванометра, а также в моменты его уменьшения или увеличения, а также при перемещении катушек друг относительно друга. Отклонения стрелки гальванометра также имеют противоположные направления при включении или выключении тока, его увеличении или уменьшении, приближении или удалении катушек.

Э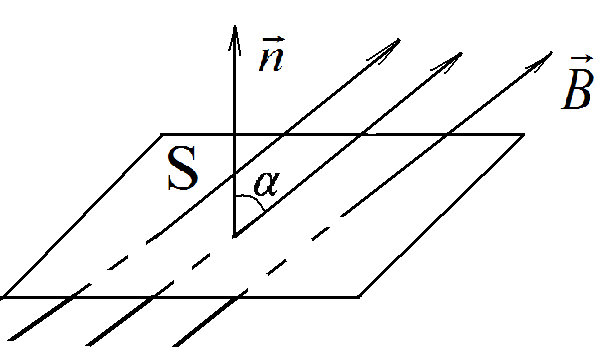то явление, открытое Фарадеем, называется явлением электромагнитной индукции. А электрический ток, возникающий при этом, называется индукционным током. Для объяснения и описания этого явления введем понятие магнитного потока (потока вектора магнитной индукции ).

Магнитным потоком через плоскую поверхность площадью S в однородном магнитном поле называют скалярную величину равную скалярному произведению вектора магнитной индукции на вектор . . Здесь где α – угол между нормалью к площадке и вектором , B_n – проекция вектора на направление нормали к площадке S. Измеряется магнитный поток в веберах (Вб).

Для произвольного магнитного поля и произвольной поверхности необходимо разбить эту поверхность на бесконечно малые элементы dS таким образом, чтобы каждый элемент dS можно было рассматривать как плоскую площадку, а магнитное поле вблизи этого элемента считать однородным. Тогда полный поток через произвольную поверхность S в произвольном магнитном поле определяется по формуле: .

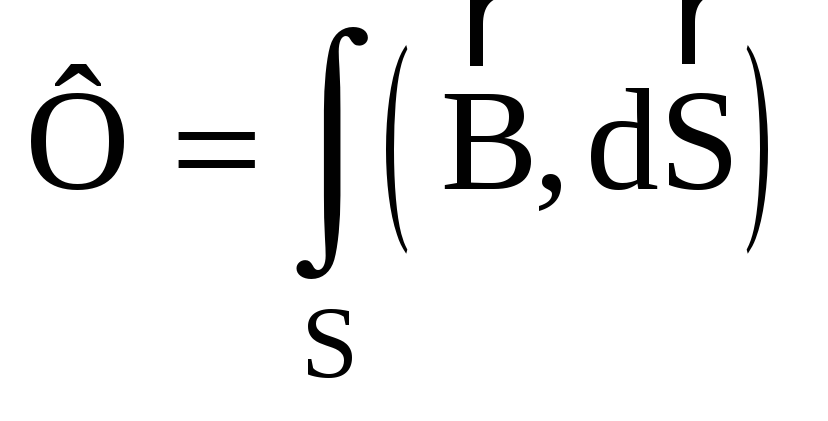Исследуя результаты своих многочисленных опытов, Фарадей пришел к заключению, что индукционный ток возникает всегда, когда в опыте осуществляется изменение сцепленного с контуром магнитного потока. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также появляется индукционный ток — в этом случае индукция магнитного поля вблизи контура остается постоянной, а меняется только поток магнитной индукции сквозь контур.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, называемый индукционным.

В результате опыта было также установлено, что значение индукционного тока абсолютно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения. В опытах Фарадея доказывается, что отклонение стрелки гальванометра (сила индукционного тока) тем больше, чем больше скорость движения магнита, или скорость изменения силы тока, или скорость движения катушек. Возникновение индукционного тока в контуре означает появление ЭДС индукции.

Закон Фарадея: какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС индукции пропорциональна скорости изменения магнитного потока через площадь, ограниченную контуром: 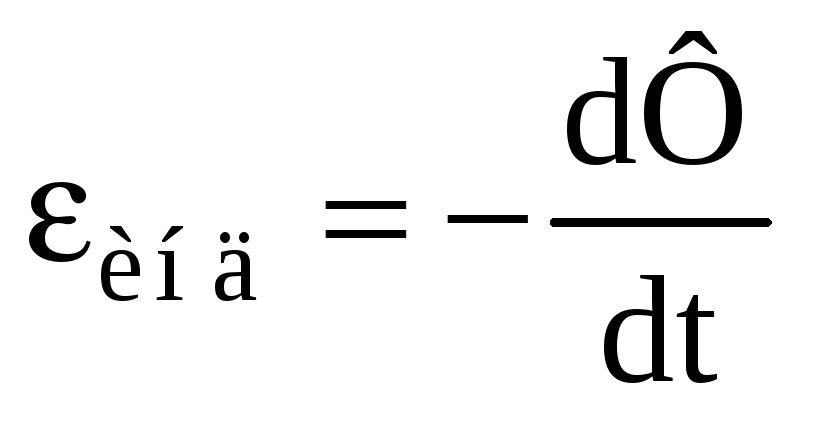. Направление индукционного тока определяется по правилу Ленца: индукционный ток направлен так, что он противодействует причине, его вызывающей. Другими словами: индукционный ток всегда имеет такое направление, при котором его магнитное поле противодействует изменению магнитного потока, вызывающего появление индукционного тока. Об этом говорит знак минус в законе электромагнитной индукции Фарадея.

Итак, при всяком изменении магнитного потока, пронизывающего замкнутый проводящий контур, в нем возникает ЭДС индукции и вследствие этого появляется индукционный ток. С другой стороны, ЭДС в любой цепи возникает только, если в ней на заряды действуют сторонние силы, т.е. силы не электростатического происхождения. Рассмотрим природу сторонних сил в случае ЭДС индукции.

Опыт показывает, что ЭДС индукции не зависит от рода вещества проводника и от его состояния. Следовательно, сторонние силы не связаны с изменением свойств проводника в магнитном поле, а обусловлены самим магнитным полем. Максвелл пришел к выводу, что причина появления ЭДС индукции состоит в возникновении электрического поля при всяком изменении магнитного поля. Под действием этого электрического поля свободные заряды проводника приходят в движение и, если проводник замкнутый, появляется индукционный ток. При этом проводники играют второстепенную роль и являются только своего рода прибором, обнаруживающим возникающее электрическое поле. Существенно, что возникающее электрическое поле не является электростатическим. Известно, что циркуляция вектора электрической напряженности в электростатическом поле по замкнутому контуру равна нулю . По этой причине электростатическое поле не может поддерживать замкнутое движение зарядов и, следовательно, не может привести к возникновению ЭДС.

Напротив, электрическое поле, возникающее при электромагнитной индукции, является вихревым. Т.е. работа по перемещению заряда в вихревом электрическом поле вдоль замкнутого пути не равна нулю. Работа по перемещению заряда между двумя какими-либо точками поля не определяется только положением этих точек, а зависит от формы пути, соединяющего эти точки. Вихревое электрическое поле вызывает в проводнике движение свободных зарядов по замкнутым траекториям, и приводит к возникновению ЭДС. При этом сторонними силами являются силы, действующие на заряды со стороны вихревого электрического поля. Циркуляция поля сторонних сил по замкнутому контуру равна ЭДС индукции . ЭДС индукции не локализована в каком-либо участке цепи, а развивается во всей цепи, где изменяется магнитный поток.

Ф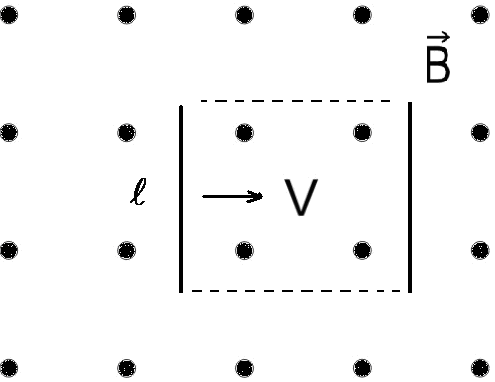ормула выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся в магнитном поле. ЭДС может быть обусловлена как изменением вектора во времени, так и движением контура относительно магнитного поля (или его деформацией). ЭДС индукции возникает в незамкнутом проводнике, если он движется в магнитном поле, пересекая линии магнитной индукции (на рисунке скорость перпендикулярна вектору ). За время dt проводник «заметает» магнитный поток , где – скорость движения проводника,. Следовательно, ЭДС индукции, возникающая в проводнике 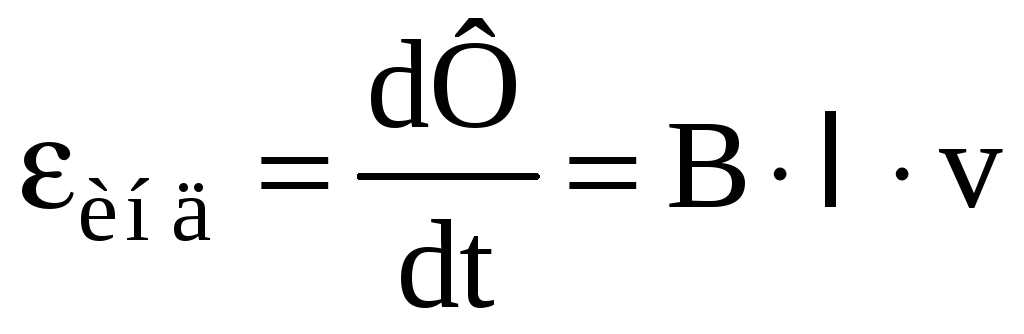. В этом случае роль сторонних сил играют силы Лоренца, действующие на заряды в проводнике. Индукционного тока в незамкнутом проводнике нет.

Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий контур. В частности, этот поток может создаваться током, текущим в самом рассматриваемом контуре. При изменении силы тока в контуре изменяется магнитный поток, создаваемый этим током. Таким образом, проводник находится в своем собственном переменном магнитном поле, которое вызывает возникновение в нем ЭДС. Это явление назвали явлением самоиндукции.

Возникновение ЭДС индукции в проводящем контуре при изменении в нём силы тока называется самоиндукцией. Возникающую при этом ЭДС называют ЭДС самоиндукции и индукционный ток – током самоиндукции.

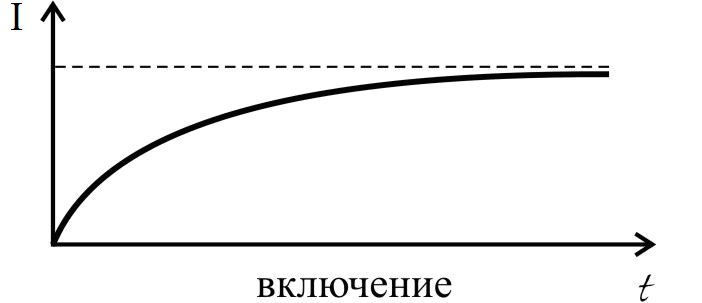
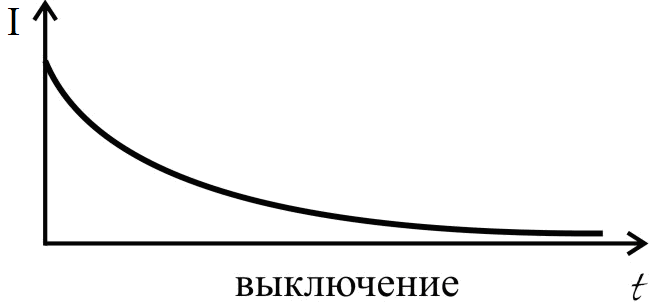
Ток самоиндукции, в соответствии с законом Ленца, направлен так, что он препятствует изменению основного тока. Если основной ток в контуре увеличивается, то ток самоиндукции направлен противоположно основному току. Если же ток в контуре уменьшается, то ток самоиндукции направлен так же, как основной ток. При включении в цепь источника тока ток самоиндукции направлен противоположно току, создаваемому источником. При выключении источника ток самоиндукции направлен так же, как и ослабевающий ток источника. Это проявляется в замедлении процессов установления и исчезновения тока.

Согласно закону Био-Савара-Лапласа величина магнитной индукции B пропорциональна силе тока , вызвавшего это магнитное поле. Поэтому магнитный поток, создаваемый током в контуре, пропорционален силе тока . Здесь L – коэффициент самоиндукции или индуктивность контура. Применяя к явлению самоиндукции основной закон электромагнитной индукции, получаем 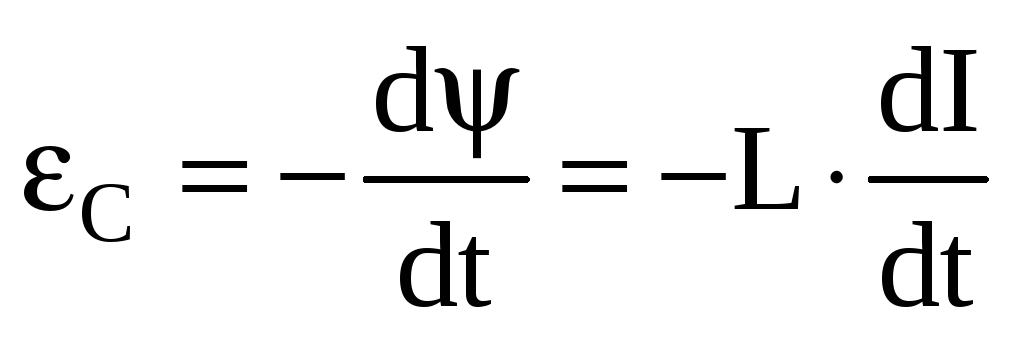, ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре. Единица индуктивности L в СИ .

При протекании по проводам постоянного тока вся работа, совершенная источником ЭДС, идет на выделение джоулева тепла. Иначе обстоит дело при возрастающих или убывающих токах.

При возрастании тока в контуре возникает ЭДС самоиндукции, направленная против ЭДС, возбуждающей ток. В результате сила тока будет меньше и только часть работы, совершенной внешней ЭДС, пойдет на выделение джоулева тепла, остальная часть – на образование энергии магнитного поля.

При уменьшении силы тока в контуре возникает ЭДС самоиндукции того же направления, что и внешняя, ток оказывается сильнее, в цепи выделяется больше джоулева тепла, чем должно было бы выделиться при данной внешней ЭДС. Это дополнительное выделение тепла происходит за счет магнитной энергии, запасенной в контуре.

Для подсчета магнитной энергии рассмотрим контур с индуктивностью L, в котором сила тока возрастает от нуля до конечного значения . При возрастании тока в контуре возникает ЭДС самоиндукции . Работа против этой ЭДС, совершаемая источником тока, идет на образование энергии магнитного поля. Если в данный момент сила тока в цепи , то мощность, развиваемая ЭДС самоиндукции, равна , а работа, совершаемая за время dt: . Модуль ЭДС самоиндукции , поэтому.

Запас энергии магнитного поля в контуре W_м равен работе, совершаемой при возрастании тока от нуля до некоторого значения .

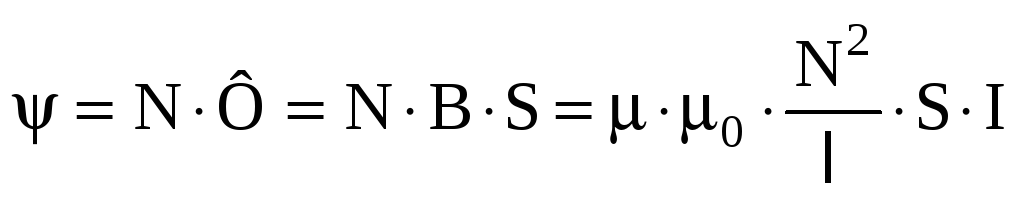Найдем объемную плотность энергии магнитного поля на примере длинного соленоида. Для этого вычислим индуктивность соленоида, считая его бесконечно длинным. При протекании тока по соленоиду внутри него создается однородное магнитное поле с индукцией , где – длина соленоида, N – число витков, - магнитная проницаемость сердечника. Полный магнитный поток через все витки соленоида , где S –площадь поперечного сечения соленоида. С другой стороны, для соленоида . 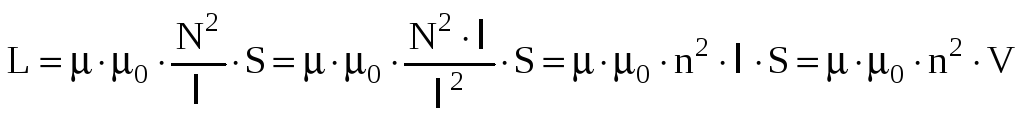Приравнивая правые части полученных выражений, получаем выражение для индуктивности соленоида , где – объем соленоида.

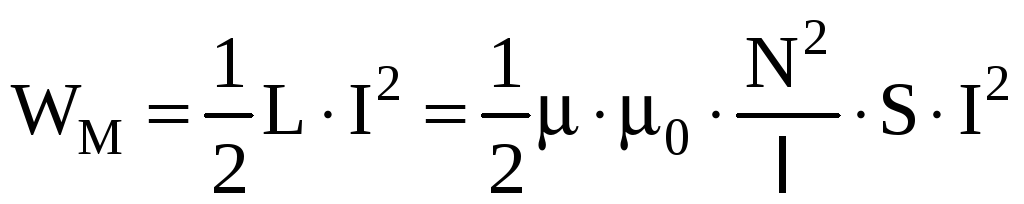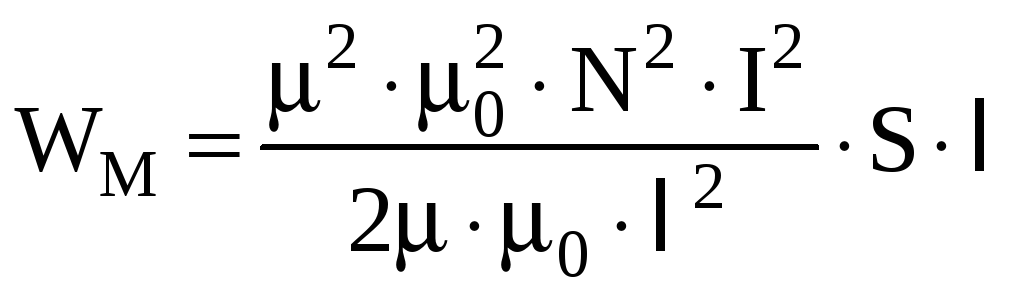Подставим выражение для индуктивности соленоида в формулу энергии магнитного поля . Умножим и поделим на это выражение. Так как , то 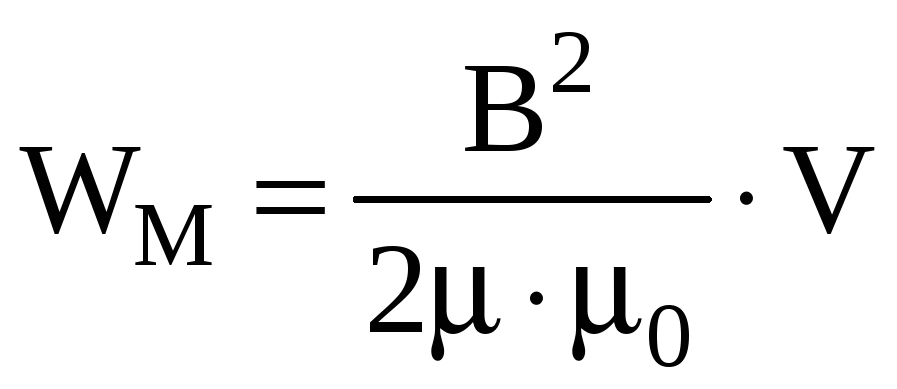. Отсюда 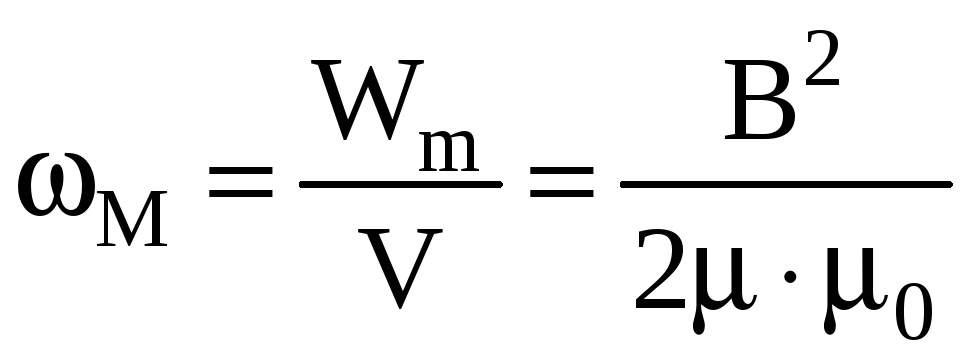– энергия единицы объема магнитного поля или объёмная плотность энергии.

9