
220.1 220.2220.3220.4
221.
1)
уравнение касательной: 
 уравнение
нормали:
уравнение
нормали: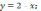
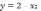 точки пересечения касательной с осями
координат:
точки пересечения касательной с осями
координат:

2)
уравнение касательной: 
 уравнение
нормали:
уравнение
нормали:
 точки пересечения касательной с осями
координат:
точки пересечения касательной с осями
координат:

3)
уравнение касательной:
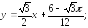

 уравнение
нормали:
уравнение
нормали:


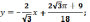 точки пересечения касательной с осями
координат:
точки пересечения касательной с осями
координат: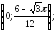

222.
В точке 
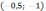 угловой коэффициент
угловой коэффициент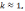
 следовательно, касательная имеет вид:
следовательно, касательная имеет вид:

В
точке 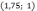
 угловой коэффициент
угловой коэффициент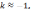
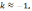 следовательно, уравнение касательной
имеет вид:
следовательно, уравнение касательной
имеет вид:
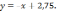
223.1
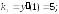
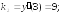
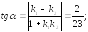
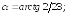
223.2

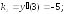
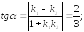

223.3





224.1
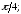 224.2
224.2 224.3
224.3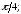 224.4
224.4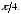
225.
1)
Графики функций
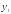 и
и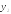

 пересекаются
в двух точках с абсциссами
пересекаются
в двух точках с абсциссами
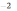 и х=3.
и х=3.
Острый
угол между графиками этих функций в
точке 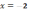
 равен
равен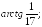
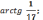
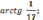 в точке
в точке
 угол равен
угол равен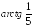
 .
.
2)
Графики функций
 и
и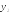 пересекаются в точке с абсциссой 0 под
углом
пересекаются в точке с абсциссой 0 под
углом
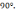
3)
Графики функций
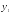 и
и пересекаются в точке с абсциссой 1 под
углом
пересекаются в точке с абсциссой 1 под
углом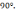
226.


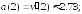

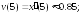
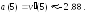
226.1
 226.2
226.2
227.1
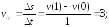

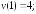 227.2
227.2
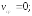

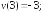
227.3


 227.4
227.4

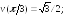
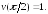
228.
Скорости совпадают т.е. 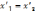 при
при
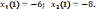
229.1
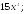 229.2
229.2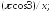 229.3
229.3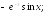 229.4
229.4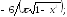
229.5
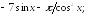 229.6
229.6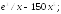 229.7
229.7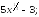
229.8
 229.9
229.9 229.10
229.10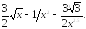
230.1
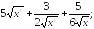 230.2
230.2

230.3
 230.4
230.4
230.5
 230.6
230.6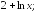 230.7
230.7
230.8.
 230.9
230.9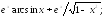
230.10
 230.11
230.11 230.12
230.12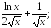
230.13
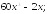 230.14
230.14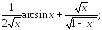 230.15
230.15
231.1
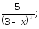 231.2
231.2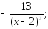 231.3
231.3 231.4
231.4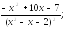
231.5
 231.6
231.6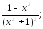 231.7
231.7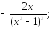 231.8
231.8
232.
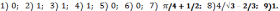
233.
1

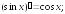 233.2
233.2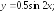

233.3

 233.4
233.4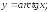
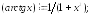
233.5
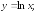
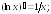 233.6
233.6

233.7

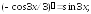
233.8
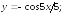
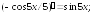 233.9
233.9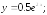

234.
Вычислим 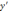 и вместе с
и вместе с подставим в данное уравнение.
подставим в данное уравнение.
234.1

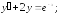
 ;
;
234.2
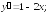
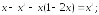

234.3
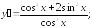
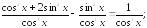

235.1
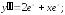 235.2
235.2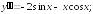 235.3
235.3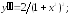
235.4
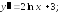 235.5
235.5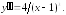
236.
Вычислим  и
вместе с
и
вместе с подставим в данное уравнение.
подставим в данное уравнение.

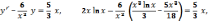
237.1
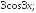 237.2
237.2 237.3
237.3 237.4
237.4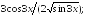
237.5
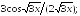 237.6
237.6
237.7
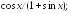 237.8
237.8 237.9
237.9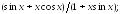
237.10
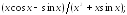 237.11
237.11
237.12
 237.13
237.13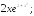 237.14
237.14 237.15
237.15
237.16
 237.17
237.17 237.18
237.18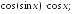
237.19
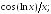 237.20
237.20 237.21
237.21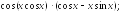
237.22
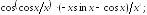 237.23
237.23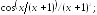
237.24
 237.25
237.25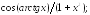 237.26
237.26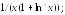
237.27
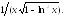
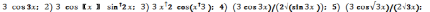
 238.1
238.1
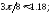 238.2
238.2 238.3
238.3
239.
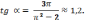
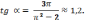
240.
1) Рассмотрим функцию 
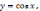 обратная к ней:
обратная к ней:
 .
Пользуясь теоремой о производной
обратной функции, имеем:
.
Пользуясь теоремой о производной
обратной функции, имеем:
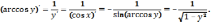
2)
Рассмотрим функцию 
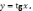 обратная к ней:
обратная к ней:
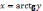 .
Пользуясь теоремой о производной
обратной функции, имеем:
.
Пользуясь теоремой о производной
обратной функции, имеем:

241.1
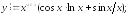
241.2
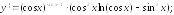
241.3
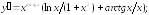
241.4

242.
1)
Преобразуем параметрическую форму
записи, исключив 
 Для этого возведем в квадрат
Для этого возведем в квадрат
 и
и
 ,
разделим первое уравнение на 4, а второе
на 9 и сложим их:
,
разделим первое уравнение на 4, а второе
на 9 и сложим их:

2)

3)
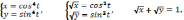
243.1
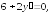
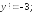 243.2
243.2 243.3
243.3
243.4
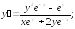 243.5
243.5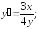 243.6
243.6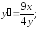 243.7
243.7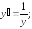
243.8
 243.9
243.9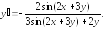
244.1

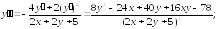
244.2
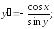
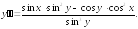
245.


246.1

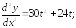 246.2
246.2

246.3
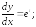
 246.4
246.4
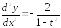 .
.
247.1

Угловой
коэффициент равен нулю, значит, уравнение
касательной имеет вид: 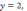
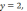 а нормали
а нормали
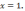
247.2

 247.3
247.3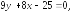
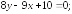

 247.4
247.4
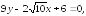
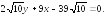
248.1

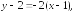
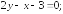
248.2
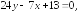
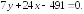
249.1
 249.2
249.2 249.3
249.3
249.4
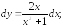 249.5
249.5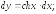 249.6
249.6
249.7
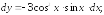 249.8
249.8 249.9
249.9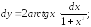
249.10
 249.11
249.11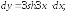
249.12

250.
 С
другой стороны
С
другой стороны


 Следовательно, равенство неверно.
Следовательно, равенство неверно.
251.1
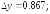
 251.2
251.2
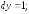
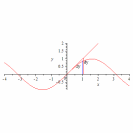
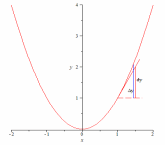
251.3
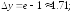
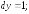 251.4
251.4



252.1
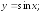


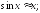
252.2
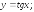


252.3

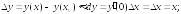

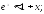
252.4
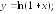

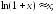
252.5




253.
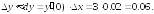
254.
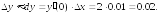
255.1
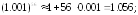

255.2


255.3
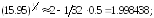

255.4
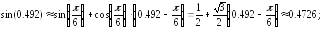

256.1
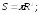
 256.2
256.2
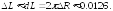
257.
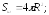

258.
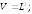



259.1
Существует число 
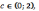 такое что
такое что
 Найдем это число.
Найдем это число.

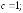 259.2
259.2

259.3
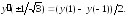
260.
1
 По
правилу Лопиталя
По
правилу Лопиталя

 260.2
260.2
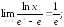 260.3
260.3 260.4
260.4
260.5
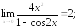 260.6
260.6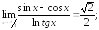 260.70;
260.8
0.5; 260.9
1.
260.70;
260.8
0.5; 260.9
1.
261.
1) 0; 
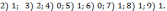
262.
1)
Прямая 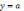
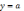 является горизонтальной асимптотой,
если
является горизонтальной асимптотой,
если
 .
.
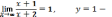
 горизонтальная
асимптота.
горизонтальная
асимптота. 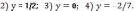
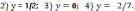
263.
1) Если предел 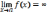
 ,
то прямая
,
то прямая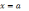
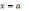 является
вертикальной асимптотой.
является
вертикальной асимптотой.
 вертикальная
асимптота.
вертикальная
асимптота.
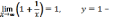 горизонтальная асимптота.
горизонтальная асимптота.
 вертикальная
асимптота,
вертикальная
асимптота, 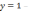 горизонтальная асимптота.
горизонтальная асимптота.
 вертикальная
асимптота,
вертикальная
асимптота, 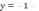 горизонтальная асимптота.
горизонтальная асимптота.
264.
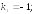
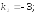
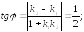

265.
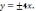
266.
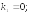

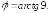 267.
267. .
268.
.
268.

269.
 .
270.
.
270.
 271.1
271.1
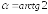 в точке (0;0),
в точке (0;0),
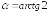 в
точке
в
точке
 271.2
271.2
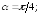 в точке (0;0),
в точке (0;0),
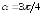 в точке
в точке
272.
 273.
273.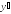 убывает.
274.
убывает.
274.
 возрастает.
возрастает.
275.1 275.2 275.3
276.1
276.2
276.3


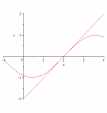
276.4 277

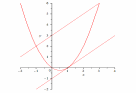 М(3;6).
М(3;6).
278.

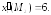 279.1
279.1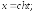

 т.е.
т.е.




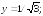
279.2
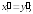

 279.3
279.3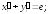
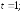
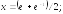
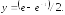
280.
 281.1
281.1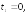
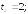 281.2
281.2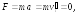
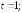
281.3

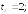 282.1возрастает
на интервалах
282.1возрастает
на интервалах
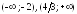 ,
убывает на
,
убывает на 282.2
убывает
на интервалах
282.2
убывает
на интервалах
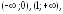 возрастает на
возрастает на
282.3
убывает
на интервалах
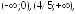 возрастает на
возрастает на
282.4
возрастает
на интервалах
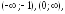 убывает на
убывает на
282.5
возрастает
на интервалах
 убывает на
убывает на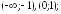
282.6
возрастает
на интервалах
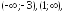 убывает на
убывает на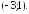
283.1
возрастает
на интервале
 убывает на
убывает на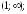
283.2
убывает на интервалах
 возрастает на
возрастает на
283.3
убывает
на интервалах
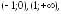 возрастает на
возрастает на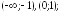
283.4
возрастает
на интервале
 ,
убывает на
,
убывает на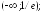
283.5
возрастает
на интервале
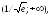 ,
убывает на
,
убывает на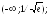
283.6
возрастает
на интервале
 ,
убывает на
,
убывает на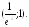
284.1 min (2;-1); 284.2 max(1;-4); 284.3 min (0;0); max(1;1); 284.4 min (-1;3);
min
(4;-128); max(0;0); 284.5
max
(1;0); min (5/3;44/3); 284.6
min(- -64);
-64);
min(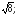 -64);max
(0;0).
-64);max
(0;0).
285.
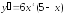 ;
;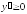 на (-
на (- и
и
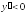 на
(5;
на
(5;
286.
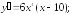
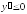 на
(
на
(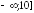 и
и
 на
(10;
на
(10; .
.
287.1 min (-1;-1/e); 287.2 min (0;0), max (-2;4/e2); 287.3 min (0;0); 287.4 max(0;1);
287.5
min
(-1;-1/2), max (1;1/2); 287.6
min(1/e;
-1/e); 287.7
min(1/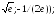
287.8
min
(1;0), max
(e-2;4/e2).
288.
Т.е
доказать, что
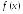 выпукла вниз, т.е.
выпукла вниз, т.е.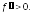
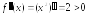 ч.т.д.
ч.т.д.
289.1
точка
перегиба (1;0), выпукл вверх на (- выпукл вниз на (1;
выпукл вниз на (1; );
);
289.2
точка
перегиба (3;-648), выпукл вниз на (3; выпукл вверх на (-
выпукл вверх на (- ;0),(0;3);
;0),(0;3);
289.3
точка
перегиба (1/3;-119/27), выпукл вверх на (-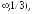 выпукл вниз на (1/3;
выпукл вниз на (1/3; ).
).
290.1
точки
перегиба х1=-1/ и х2=1/
и х2=1/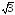 ,
выпукл вверх на (
,
выпукл вверх на ( выпукл
вниз на (-
выпукл
вниз на (- ;
;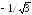 ),(
),( );
);
290.2
точки перегиба х1=--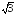 и х2=
и х2=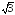 ,
выпукл вверх на (
,
выпукл вверх на ( выпукл
вниз на (-
выпукл
вниз на (- ),(
),(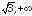 );
);
290.3
точки
перегиба х1=-1/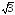 и х2=1/
и х2=1/ ,
выпукл вниз на (
,
выпукл вниз на (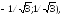 выпукл
вверх на (-
выпукл
вверх на (- ;
; ),(
),( );
);
290.4
всюду
выпукл вниз; 290.5
точки
перегиба х1=-1
и х2=1,
выпукл вверх на (-
(1; ),
выпукл вниз на(-1;1);290.6
точка
перегиба х=2, выпукл вверх на (-
),
выпукл вниз на(-1;1);290.6
точка
перегиба х=2, выпукл вверх на (-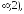
выпукл
вниз на(2;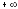 ).
).
291.
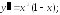
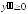 на
интервале
(
на
интервале
(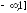 ,
, на
(1;
на
(1;
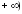 .
.
292.1 у=0 - горизонтальная асимптота.292.2 у=0 - горизонтальная асимптота;
292.3
 вертикальные асимптоты,
вертикальные асимптоты,
 - горизонтальная асимптота;
- горизонтальная асимптота;
292.4
 --
горизонтальные асимптоты; 292.5
--
горизонтальные асимптоты; 292.5
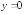 -
горизонтальная асимптота
-
горизонтальная асимптота
в левой полуплоскости;
292.6
 -
горизонтальная асимптота в правой
полуплоскости;
-
горизонтальная асимптота в правой
полуплоскости;
