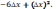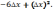173.1 173.2173.3 173.4

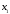
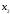
174. 1) Пусть >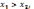, составим разность

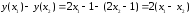
следовательно, 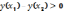т.е. функция возрастает.

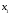
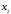
2) Пусть >составим разность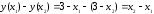

следовательно, 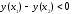т.е. функция убывает.

175. 1) убывает; 2) убывает; 3) убывает; 4) немонотонна; 5) убывает; 6) возрастает; 7) немонотонна; 8) возрастает; 9)немонотонна; 10) убывает.

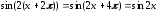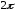176.1 , следовательно, период.

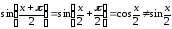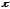176.2 , следовательно, не является периодом.

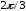176.3 , следовательно, период.

177. 1 минимум функции достигается при и равен 1.

177.2 Максимум функции равен 7 и достигается при

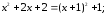
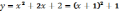
177.3 т.к. функция 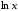монотонно возрастает, то

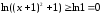
, значит экстремум исходной функции равен 0.

178.1

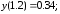
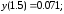
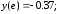
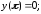
178.2

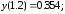
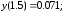
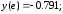
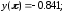
178.3

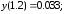
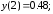
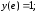
178.4

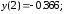
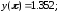
180.1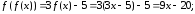 180.2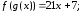

180.3 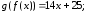180.4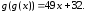

181.1 181.2

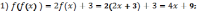
181.3 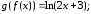181.4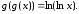

182.1 182.2 182.3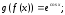

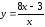
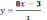
182.4 .183. Из исходной функции 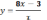выразим х:

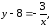
Следовательно, обратная функция имеет вид

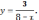
184. Из исходной функции 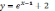выразимx:

следовательно, обратная функция имеет вид

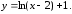
185.1 185.2

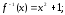
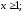
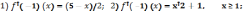185.3 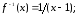185.4

187.

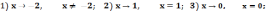
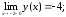
188. 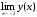- не существует.

189.1 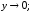189.2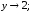189.3

190.1 190.2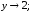190.3

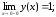
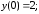
191.1 предельного значения нет.

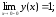
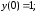
191.2 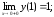предельное значение .

191.3 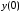-не определено; предельного значения нет.

192.1 192.2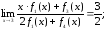

192.3 192.4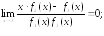

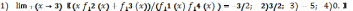
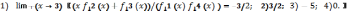
193.1 -52; 193.2 14; 193.3 0.4; 193.4 1; 193.5 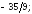193.6

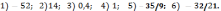
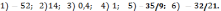194.1 -1777/60; 194.2 197/12; 194.3 -4/3; 194.4 4.5; 194.5 -3.4; 194.6 -1.2.

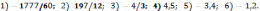195.1

195.2

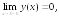
195.3

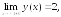
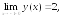
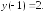
196.

197.

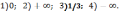
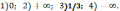
198.

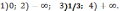
199.1 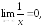следовательно, -горизонтальная асимптота.

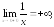следовательно, 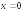- вертикальная асимптота.

199.2 следовательно, -горизонтальная асимптота.

следовательно, 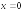- вертикальная асимптота.

200.1 200.2

200.3 200.4

200.5 200.6

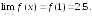
201. 1) 2; 2) 0; 3) -2,5; 4) 3; 5) 0; 6) 1,5. 202. 1) -0,5; 2) 0; 3) 1; 4) 2; 5) 0; 6)

203.1 5; 203.2 --5; 203.3 5/6; 203.4 0.25; 203.5 -1.5; 203.6 4; 203.7 -3; 203.8 0.8;

203.9 0.5; 203.10 0.25; 203.11 -2/3; 203.12 -0.75.

204. 1) 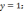2)3)

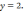
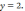
205.1 ,следовательно, - вертикальная асимптота;

205.2 205.3205.4

206. Так как функции и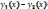непрерывны по условию, то их сумма и разность также непрерывны, следовательно, и непрерывны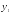и.

207.1 207.2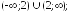207.3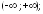207.4

207.5 207.6208. 1) 2; 2) 2.

209. 1) 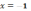точка разрыва 2-го рода; 2)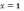точка разрыва 2-го рода;

3) функция определена и непрерывна на всей числовой прямой;

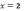
4) 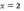точка разрыва 2-го рода; 5)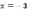точка разрыва 2-го рода;

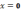
6) точка разрыва 1-го рода, устранимый разрыв.

210. 1) В точке функция терпит разрыв первого рода (скачок); в точке

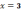функция непрерывна;

2) в точке 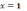функция терпит разрыв первого рода (скачок); в точке

функция непрерывна;

3) в точке 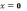функция терпит разрыв первого рода (скачок); в точке

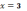
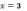функция непрерывна;

4) в точке функция терпит разрыв первого рода (скачок); в точке

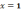функция непрерывна.

211. На интервалах функция достигает своего наибольшего и наименьшего значений.

212.1 212.2

212.3212.4

213. 1) - точка разрыва второго рода;

2) функция непрерывна;

3) 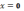- точка разрыва второго рода;

4) функция не определена.

214. В общем виде многочлен третьего порядка имеет вид .

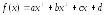Поскольку функция определена на всей числовой прямой и ,

(будем считать, для определенности, что , а, то существует хотя бы одна точкатакая, что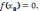

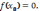
215.1 1; 215.2 3/7; 215.3 1; 215.4 1; 215.5 8; 215.6 6; 215.7 2; 215.8 1; 215.9

215.10 0; 215.11 1/3; 215.12 е²; 215.13 3; 215.14 215.15215.16

215.17 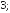215.181; 215.19 215.20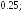215.21 5/6.

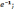
216. 1) е 2) 3)4) 1; 5) 1/7.217. 1) 218. 1) 1; 2) 1; 3) 1; 4)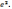

219. 1)

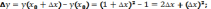
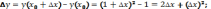
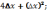
2) 3)