Информац_технологии_Черных_2000

- 91 -

N 40000 / A 1 0.0015 A ,

Где A-возраст,лет.

Таблица 5.1

Коэффициент оптимальности числа стволов

Для сосны и ели оптимальное число стволов в зависимости от класса бонитета, возраста и оптимальной относительной полноты после 70 лет можно вычислить по следующим формулам:

N опт(1 бон)= (40 1600) / A K n Р,

N опт(1 бон)= (40 1800) / A K n P ,

N опт(1 бон)= (40 2000) / A K n P,

где A-возраст,лет;

P-относительная полнота после 70лет:для 1 класса бонитета равна 0,95,для 2 класса бонитета-0,85 и 3 класса бонитета-0,75;

Kn-коеффициент оптимального числа стволов в зависимости от возраста(табл.5,1)

5.1.2.3. Стратегия рубок ухода по К.Ф.Тюрмеру

На основе исследований известный лесовод К.Ф. Тюрмер ввел правило: в древостое после рубок ухода расстояние между деревьями должно быть равно 18-20 средним диаметрам (табл. 5.2). При проведении рубок ухода необходимо стремиться к соблюдению соотношения числа стволов и среднего диаметра древостоя согласно данным после проведения расчетов для определения интенсивности из-реживания конкретного древостоя.

Таблица 5.2 Оптимальное число стволов после рубки в зависимости от среднего

диаметра древостоя по К.Ф. Тюрмеру

5.1.2.4.Стратегия рубок ухода по С.Н. Сеннову

Врезультате многолетних исследований и практического опыта

- 92 -

профессор С.Н.Сеннов предложил нормативы относительной интенсивности изреживания по запасу при рубках ухода и их повторяемости (табл.5.3).

Таблица 5.3 Показатели рубок ухода в сосновых древостоях таежной

лесорастительной зоны

5.1.3. Результаты работы имитационной модели "Сосна"

Имитационная модель С», на" реализована на алгоритмическом языке TURBO - BASIC. Для запуска программы необходимо в командной строке набрать имя программы - "SOSNA99". После запуска программы пользователь ведет диалог с ПК, отвечает на поставленные вопросы.

Врезультате имитации рубок ухода необходимо получить наибольший запас в 80 лет.

Варианты имитации студент выбирает исходя из рекомендаций С.Н.Сеннова, С.В.Белова, К.Ф.Тюрмера или «Наставлений по рубкам ухода....» [60]. После анализа результатов имитации роста сосновых древостоев пользователь выбирает собственную стратегию интенсивности изреживания древостоя.

Втабл. 5.4-5.7 приведены примеры имитации роста сосновых древостоев, произрастающих на территории Нолькинского лесничества УНПКЛП МарГТУ. Изреживание высокополнотного древостоя сосны проводилось в 55 лет и 65 лет, с выборкой по запасу 4 м3 и 167 м3.

- 93 -

Таблица 5.4

Прогноз роста соснового древостоя

Область-Марий Эл

Лесхоз-УНПКЛПМарГТУ

Лесничество-Нолькинское Квартал-112 Выдел-3 Пробная площадь№9

Таблица 5.5 Распределение числа стволов по ступеням толщины

- 94 -

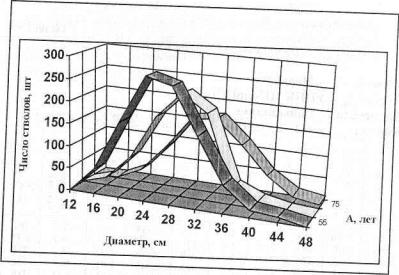
Прогноз роста сосны обыкновенной

Рис 5.1. Распределение числа стволов по ступеням толщины при прогнозе роста с учетом изреживания сосны обыкновенной

Прогноз роста соснового древостоя Область - Марий Эл Лесхоз – УНПКЛПМарГТУ

Лесничество— Нолькинское Квартал — 12 Выдел - 6 Пробная площадь № 11

Таблица 5.6

- 95 -

Таблица 5.7 Распределение числа стволов по ступеням толщины

Общая закономерность распределения числа стволов по ступеням толщины с увеличением возраста сохраняется (рис. 5.1). К возрасту 75 лет древостой имеет запас 718 м3 на 1 га и полноту 0.789.

Результаты имитации не согласуются с рекомендациями К.Ф.Тюрмера, Интенсивность изреживания была занижена. Число стволов необходимо уменьшить в два раза (табл. 5.2). Для достижения требуемого результата по прогнозу роста сосны имитацию необходимо повторить.

В таблицах 5.6 и 5.7 приведены результаты прогноза роста с выборкой по запасу в 99 лет 5 м3. Этот пример имитации роста сосны отражает закономерности роста в возрасте спелости.

Следует отметить, что при наличии рядов распределения числа стволов по ступеням толщины можно рассчитать товарную структуру будущего древостоя.

5.2. Автоматизированное построение моделей роста Древостоев

5.2.1. Теоретические сведения

Таблицы хода роста (ТХР) имеют большое значение для лесоустройства. Сведения о ходе и производительности насаждений служат основой многим лесохозяйственным расчетам. Есть несколько видов ТХР, подразделяемых по назначению:

1)ТХР нормальных насаждений;

2)ТХР модальных насаждений;

3)ТХР оптимальных насаждений;

4)ТХР с различной густотой и разными суммами площадей сечений.

ТХР предназначены:

• для характеристики и прогнозирования роста и развития древостоев;

-

• установления спелости леса и обоснования возраста рубки;

-96 -

•проектирования лесохозяйственных мероприятий;

•выявления закономерностей роста и развития древостоев;

•составления региональных таксационно-справочных нормативов и тд. В разработку методики составления таблиц хода роста внесли большой

вклад видные лесоводы страны: Орлов М.М., Варгас де Бедемар, Тюрин А.В., ТретьяковН.В., АнучинН.П, АнтанайтисВ.В., Багинский В.Ф., Бочков И.М., Галицкий В.В., Дворецкий М.Л., ДракинВ.Н., Вуевский Д.И., ЗагреевВ.В , Зейде Б.Б., Кивисте А.К., Кор-сунь Ф.Д., Кофман Г.Б., Кузьмичев В.В., Макаренко А.А., Моисеев B.C., Моисеенко Ф.П., Мошкалев А.Г., Никитин К.Е., СаликовН.Я., Свалов Н.Н. и многие другие. ЗагреевВ.В. (1971,1978) на основании 400 таблиц хода роста выявил возможность систематизации таблиц. Оказалось, что для определения хода роста сосны, например, нужна всего одна таблица с тридцатью типовыми рядами. Такие индексные таблицы (графики) служат для сравнительной оценки и группировки таблиц по степени сходства и различия в характере (типе кривых) хода роста.

Наиболее известные таблицы хода роста оптимальных насаждений составили Е. Assmann и F. Franz (1967). Одно из новшеств в таблицах заключается в том, что в пределах каждого класса бонитета введены три уровня производительности (верхний, средний и низший). ТХР составляются для каждого уровня производительности.

Ход роста описывается множеством функций хода роста, которые были сгруппированы А.К. Кивисте (1988) в семь групп и проанализированы с учетом общих закономерностей роста живых организмов.

К функциям роста предъявляются следующие требования:

1)График должен проходить через начало координат, f(x) =0 прих=0.

2)Функция роста должна быть возрастающей,/'(х) больше или равно 0

при х>0.

3)Предел функции при неограниченном возрастании аргумента должен стремиться к асимптоте: lim fix) = max x —> оо

106

4)График текущего прироста должен исходить из начала координат,/'^ =0 при х=0.

5)Функция роста должна иметь точку nepera6a,/"(xj=0 прих>0. Анализ известных функций роста позволил выбрать функцию

А. Мичерлиха (Mitscherlich). Эта функция удовлетворяет необходимым требованиям для описания общих закономерностей роста живых организмов.

Функция имеет вид:

Т мод Т мах (1 е А С1 )С2

где Т - моделируемый таксационный показатель, диаметр (см), высота (м), сумма площадей сечений (м:), запас (м3);

Т - асимптотическое значение таксационного показателя для данmax

но го естественного ряда развития древостоя;

- 97 -

А -возраст, лет; е - основание натурального логарифма;

C1 - параметр роста;

С2 - параметр формы кривой.

Кривая роста имеет S-образный вид при С2> 1 с точкой перегиба m=lnC2/Cr.

т" Если С2 находится в пределах от 0 до 1, то функция не имеет точки перегиба. Такой вид кривой хорошо описывает значения сумм площадей сечений и диаметров, a S - образный вид кривой описывает значение высот и запасов. Следовательно, для моделирования основных таксационных показателей можно использовать один вид функции, изменяя параметры роста и формы кривой.

Следует отметить, что функция А. Мичерлиха приемлема для описания динамики изменения таксационных показателей отдельного дерева и древостоя.

5.2.2. Алгоритм моделирования хода роста древостоев

Функция роста А.Мичерлиха является нелинейной по параметрам. Для поиска оптимальных параметров С; и С2 использован итерационный метод, который можно описать по этапам:

А. В каждой точке естественного ряда по возрасту для моделируемых таксационных показателей вычисляется Су. при фиксированных значениях С2 (С2 = 1,2,3,4,...,10):

- 98 -

Где Топ( А) -фактическое значение таксационного признака в возрасте

А

I=1,2,3…,n;n-число наблюдений

Б.По наименьшей абсолютной ошибке функции выбирается значение параметра С2,которое принимается за константу.

В.При постоянном значении параметра С2 производится сглаживание параметра С1 для всех точек естественногои ряда по полиному третьей степени,С1=f(A).

Г.Параметр С2 расчиываем по уравнению:

Где С’1-расчетные значения параметра С1 по полиному третьей степени. Д.Производится сглаживание параметра С2 по полиному третьей

степени,С2=f(A).

Е.Для моделируемого таксационного показателя решается задача поиска значения асимптоты при минимальной среднеквадратической ошибке

(m) на отрезке [a,b], F(X,C1,C)=Tвыкi m=((Tвычi-Ton)^2)/n-->min,где n-число экспериментальных значений моделируемого таксационнго показателя;Т м' ах-

наибольшее значение таксационного показателя из n экпериментальных

точек; a Tmax' 1.05; b Tmax' 1.30.

Оптимальное значение асимптоты таксационного показателя определяется по методу золотого сечения, который реализуется по следующему алгоритму:

1.Вычисляется коэффициент дробления отрезка [а,b], К=(5^1/2- 1)/2=0.6180339.

2.Вычисляется абсцисса Х1=а+(1-К)'(Ъ-а) и вычисляется F(X1,C1,C). Cj и С2 определяются согласно п. А.

3.Вычисляется абсциссаХ2=а+К'(b-а).

4.Проверяется условие (X2-XJ<E, где Е - заданная погрешность вычисления Хт При выполнении этого условия вычисляется Xm=(X; +XJ/2 yiF(Xm,CyCJ и останавливается счет.

Если условие не выполняется, идѐм к п. 5.

5.EcmFpCj. С;}, С) < F(X2, С,, С), то а=Хг Х=Х2, F(Xy Cp CJ = F(X2,

С,, С2) и идем к п. 3 и п. 4.

6.Если^(Т7, C]t CJ > F(XT Cj, CJ, то b=X, X2=X, f(X? Cr CJ =f(Xr CJ: CJ идѐм к п. 2 и п. 4.

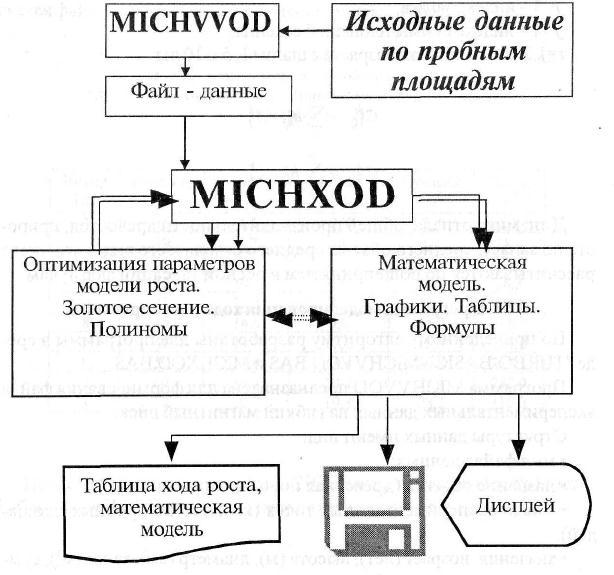
- 99 -

Рис. 5.2. Модельная структура программы MICHXOD

Ж. Моделированию подвергаются четыре таксационных показателя: средний диаметр, средняя высота, сумма площадей сечений и запас.

- 100 -

Модель хода роста древостоя элемента леса принимает вид:

Tij Tmax (1 e A C1 y )C2 y ,

Гдеj=1-индекс высоты; J=2-индекс диаметра; J=3-индекс запаса;

J=4-индекс суммы площадей сечения; I=1,2,3…,n-индекс возраста с шагом 1,5 и 10 лет.

3

С1кij bkj' Akj ,

0

3

C2kij bkj'' Akj

0

Динамика отпада, общей производительности древостоя, прироста по запасу, среднего объема среднего ствола и его видового числа рассчитываются по общепринятым в лесной таксации формулам.

5.2.3. Программа моделирования хода роста древостоя

По приведенному алгоритму разработаны две программы в среде

"TURBO-BASIC'-MICHVVOD.BAS hMICHXOD.BAS.

Программа MICHVVOD предназначена для формирования файла экспериментальных данных на гибкий магнитный диск.

Структуры данных имеют вид:

•имя файла данных;

•название объекта (древесная порода, тип леса и т. д.);

•число экспериментальных точек (количество пробных площадей);

•значения: возраст (лет), высота (м), диаметр (см), запас (м3), сумма площадей сечений (м2).

Программа MICHXOD предназначена для автоматизированного построения модели хода роста древостоя на базе функции Мичерли-ха.

Модельная структура программы приведена на рис 5.2. Программа занимает 72 Кбайт дисковой памяти. Время счета по одному естественному ряду 1... 2 минуты.