Ошибки репрезентативности (представительности)

В результате изменчивости (варьирования) изучаемого признака, между статистическими показателями выборочной совокупности и генеральной, могут наблюдаться некоторые расхождения, которые являются случайными ошибками выборки и называют основными ошибками репрезентативности того или иного статистического показателя.

Ошибка средней величины:.

Например: .

Ошибка стандартного отклонения:.

Например: .

Ошибка коэффициента вариации:.

Например: .

Ошибка точности:.

Например: .

Точность опыта (относительная ошибка опыта)

Показатель точности опыта выражает величину ошибки средней величины в процентах от самой средней. Точность опыта или процент ошибки наблюдения – это процент расхождения между генеральной и выборочной средней.

Чем меньше показатель процента ошибки, тем точность опыта выше.

Точность опыта считается удовлетворительной, если численное значение данного показателя не превышает 5 %. Если показатель точности больше 5 % , то рекомендуется увеличить число наблюдений или число повторностей. Точность опыта можно повысить (численное значение соответственно снизить) путём повышения точности измерений объектов опыта.

или .

Например: .

Достоверность статистических показателей (надежность)

Достоверность – это то, что не может вызвать сомнение.

Степень надёжности статистического показателя – это достоверность. Оценку надёжности производят по t – критерию Стьюдента, который определяется как частное от деления величины статистического показателя к его ошибке репрезентативности. Это отношение должно быть ≥ 3. Если расчётное значение критерия равно или больше трёх, то значение статистического показателя достоверно и его можно использовать для сопоставлений и выводов. Если же расчётное значение критерия меньше трёх, то данный показатель можно считать ненадёжным, величина его не достоверна и она в той или иной мере вероятна.

Достоверность средней величины:.

Например: .

Достоверность стандартного отклонения: .

Например: .

Достоверность коэффициента вариации: .

Например: .

Достоверность точности: .

Например: .

Доверительный интервал для генеральной средней

ДИГС – интервал нахождения средней величины для всей генеральной совокупности.

Чем меньше расстояние между точками интервала, тем точнее выборочная совокупность характеризует генеральные параметры.

,

где t₀₅ – критерий Стьюдента на 5% уровне значимости, определяется по числу степеней свободы (из приложения учебника).

Число степеней свободы – это число свободно варьирующих вариант (k) k = n – 1

Для приведённого примера k = 30 – 1=29.

Тогда в соответствии с найденным числом степеней свободы 29 теоретическое значение критерия Стьюдента будет равно t₀₅ = 2,045. Далее производим расчёт ДИГС.

Например: ДИГС 31,08 ± 0,85 × 2,045;

ДИГС 29,34 ÷ 32,82 мм.

Необходимое число наблюдений для будущих исследований

В исследованиях можно встретить случаи, когда изучаемая совокупность имеет неизвестную численность. Тогда достаточный объём выборки из такой совокупности можно определить по формуле:

,

где C_v – расчетный коэффициент вариации;

p – заданная точность(в курсовой работе точность принять 2 %);

К – коэффициент порогового уровня доверительной вероятности

(К₁=1,00; К₂=1,98; К₃=2,63)

Например: C_v =15,03 %; p = 2 %;К₁=1,00; К₂=1,98; К₃=2,63

.

.

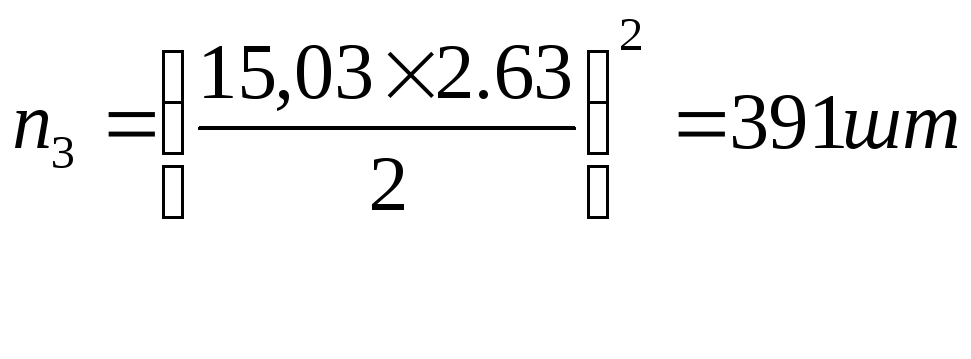
В курсовой работе рассчитать необходимое число наблюдений для будущих исследований для всех трёх пороговых уровней доверительной вероятности.