
- •Задания к контрольной работе № 1
- •1) Методом Крамера систему а);
- •2) И методом Гаусса системы а) и б)
- •Задания к контрольной работе № 2
- •1. Вычислить интегралы:
- •2. Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
- •3. Найти объем тела, образованного вращением вокруг оси фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью. Сделать чертеж.
- •5. Решить задачи:
- •6. Всхожесть семян данного сорта растений оценивается вероятностью р. Посеяно n семян. Найти:
- •8. Завод сортовых семян выпускает гибридные семена кукурузы. Вероятность того, что семя 1-го сорта равна р . Найти:
- •1) Вероятность того, что диаметр наудачу взятой детали будет больше мм и меньшемм;
- •2) Вероятность того, что диаметр наудачу взятой детали отклонится от стандартной длины не более чем на мм.
- •Контрольная работа № 3.
- •1) Записать векторы в системе орт и найти модули этих векторов;
- •2) Найти угол между векторами и;
- •3) Найти проекцию вектора на вектор;
- •4) Написать уравнение плоскости, проходящей через точку с перпендикулярно вектору .
- •1) Длины сторон ав, вс, ас;
- •Контрольная работа № 4
- •Контрольная работа № 5
- •2) Дисперсию ;
- •3) Среднее квадратическое отклонение .
- •4) Построить многоугольник распределения;
- •5) Построить функцию распределения.
- •1) Вероятность попадания случайной величины в интервал;
Задания к контрольной работе № 1
Решить системы уравнений:
1) Методом Крамера систему а);
2) И методом Гаусса системы а) и б)
1. а)
 б)
б)
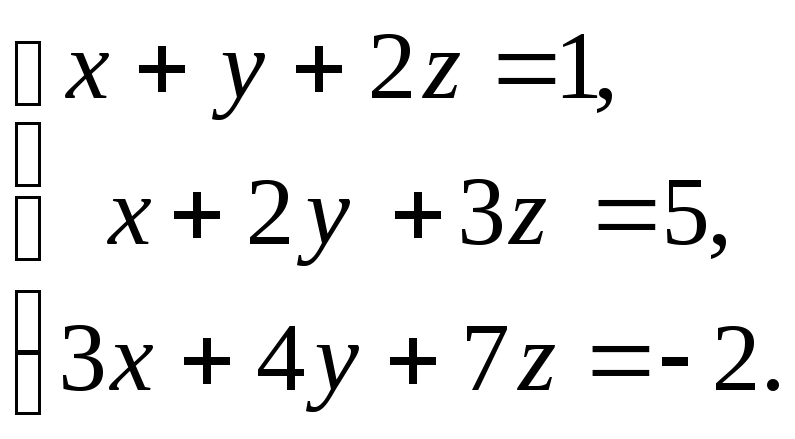
2. а)
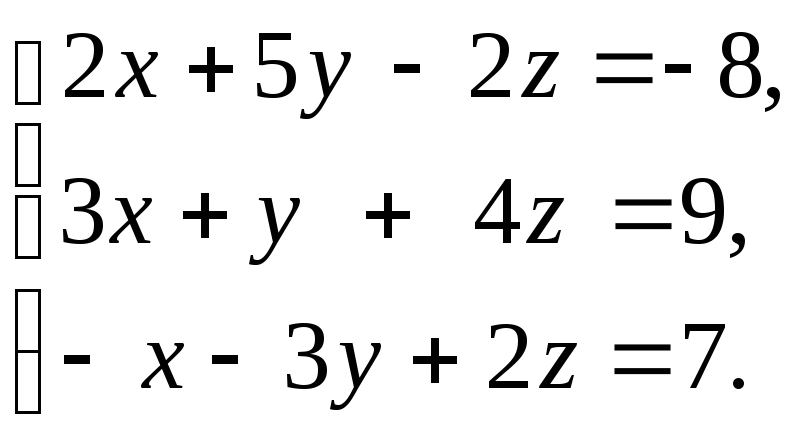 б)
б)
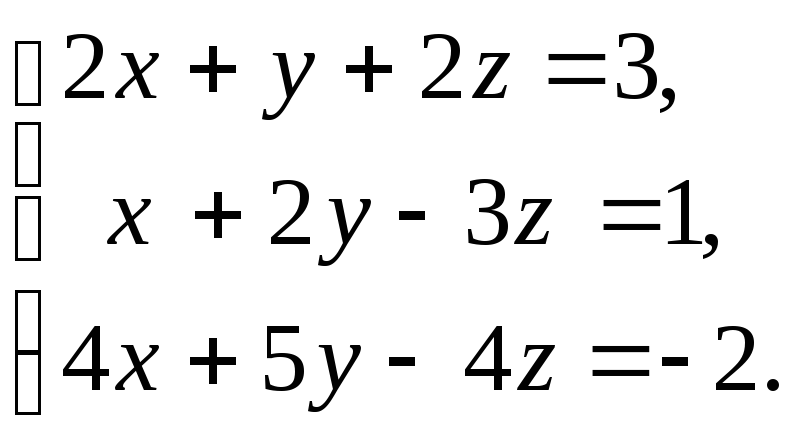
3. а)
 б)
б)
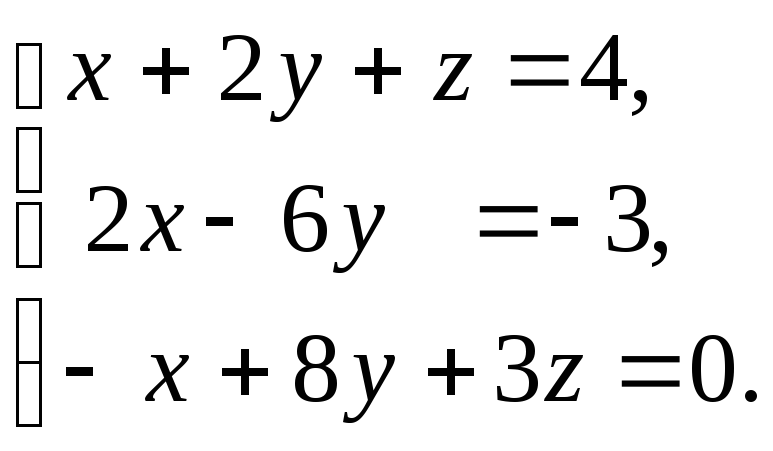
4. а)
 б)
б)

5. а)
 б)
б)
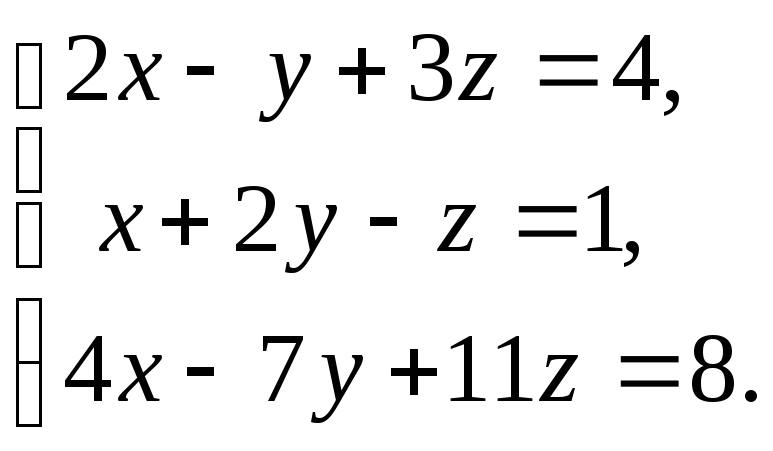
6. а)
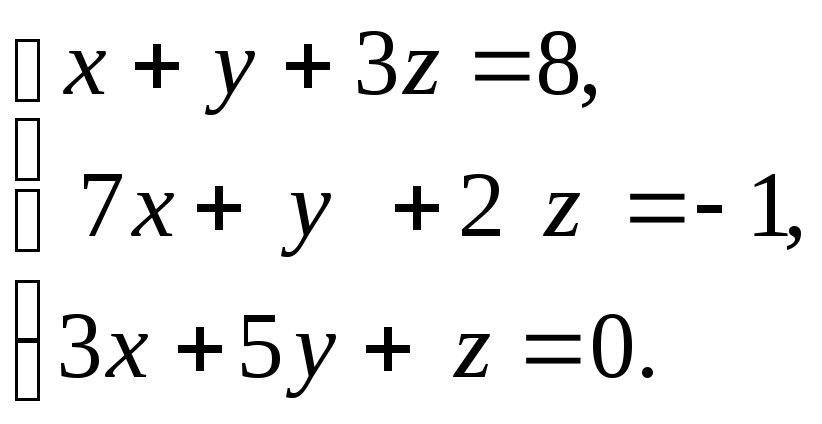 б)
б)

7. а)
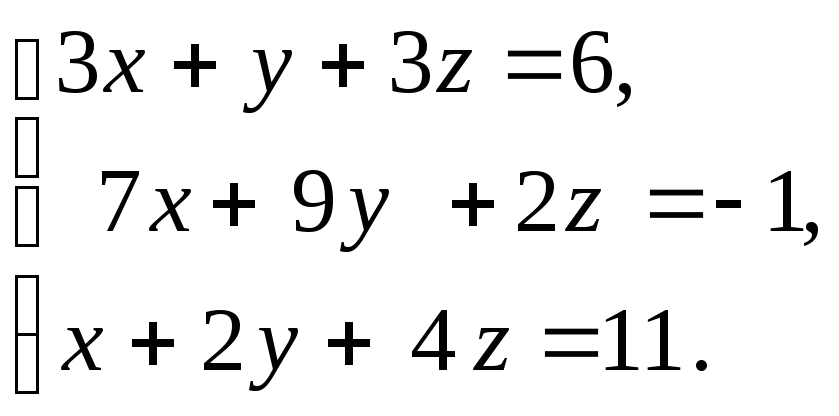 б)
б)
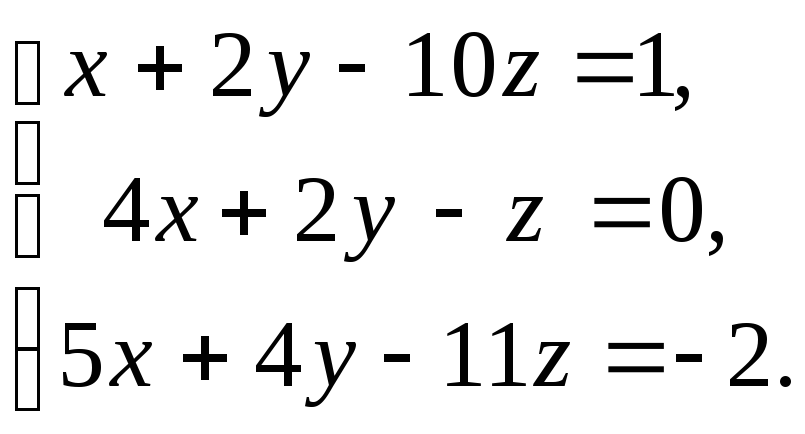
8. а)
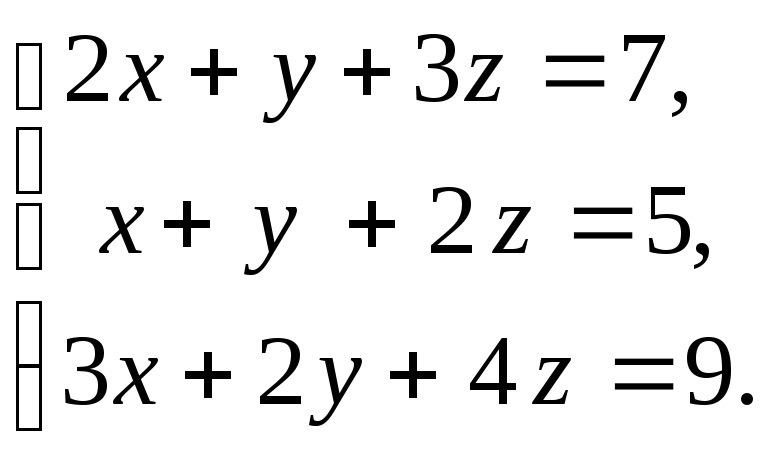 б)
б)
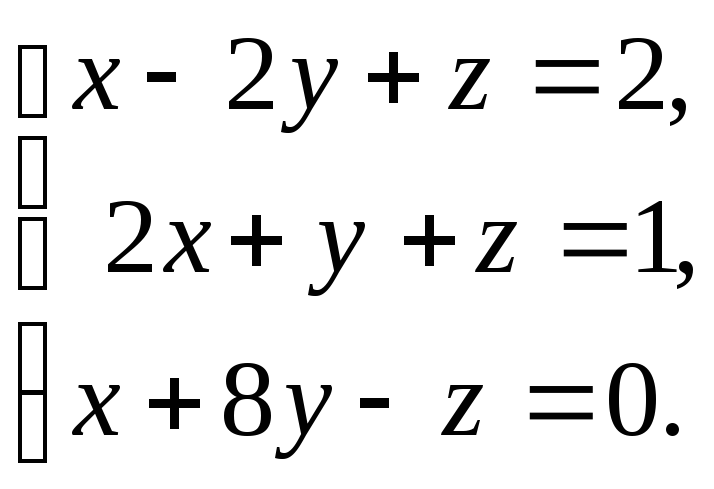
9. а)
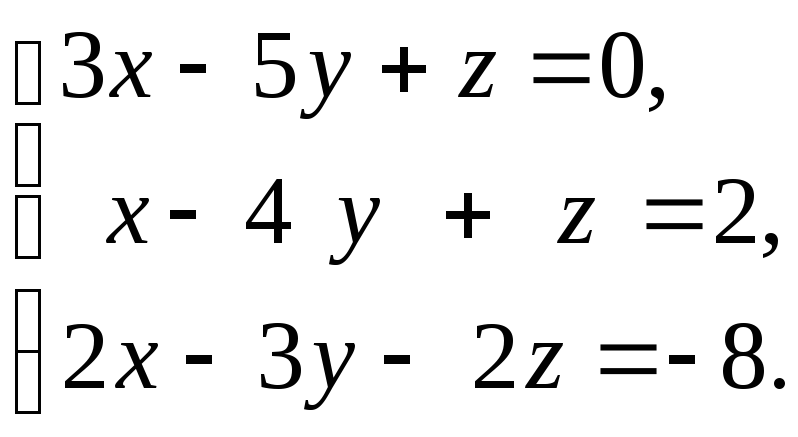 б)
б)
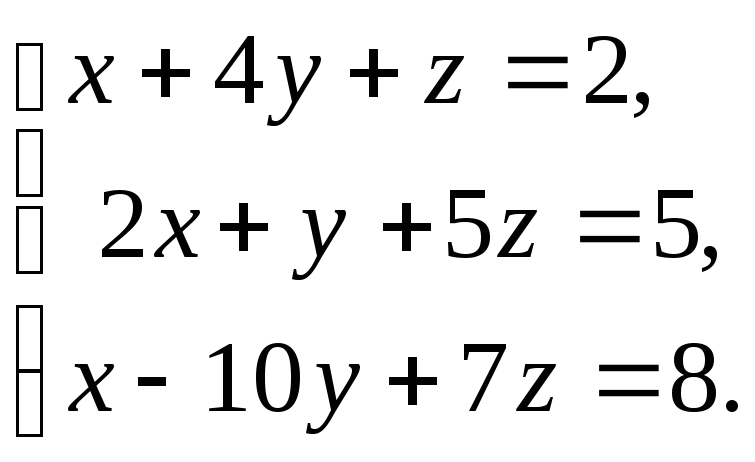
10. а)
 б)
б)

11. а)
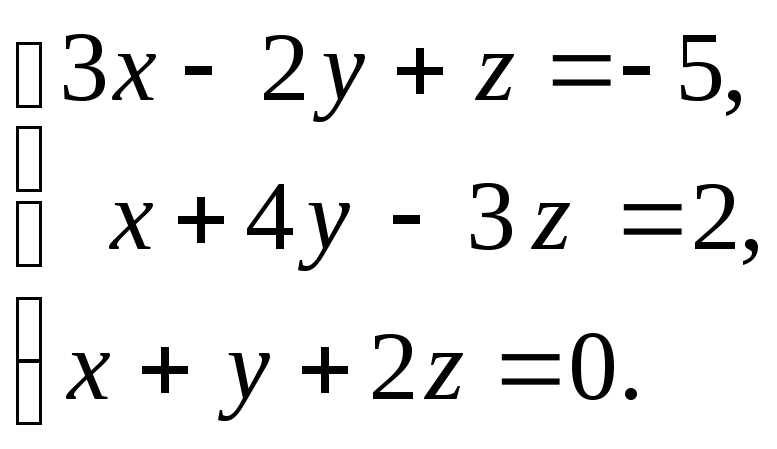 б)
б)
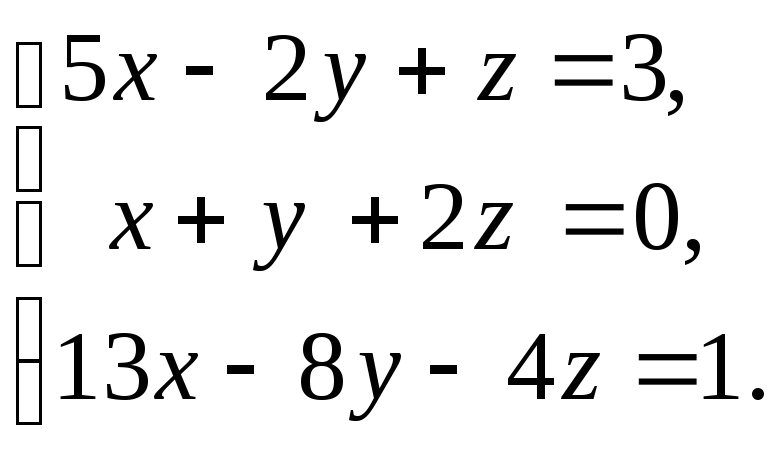
12. а)
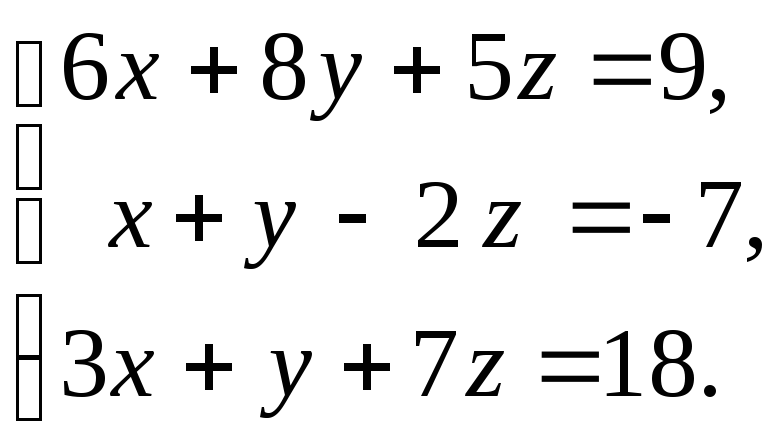 б)
б)

13. а)
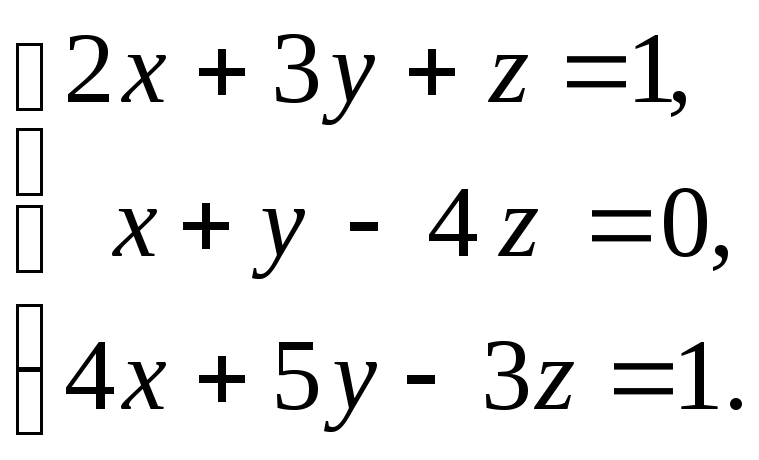 б)
б)

14. а)
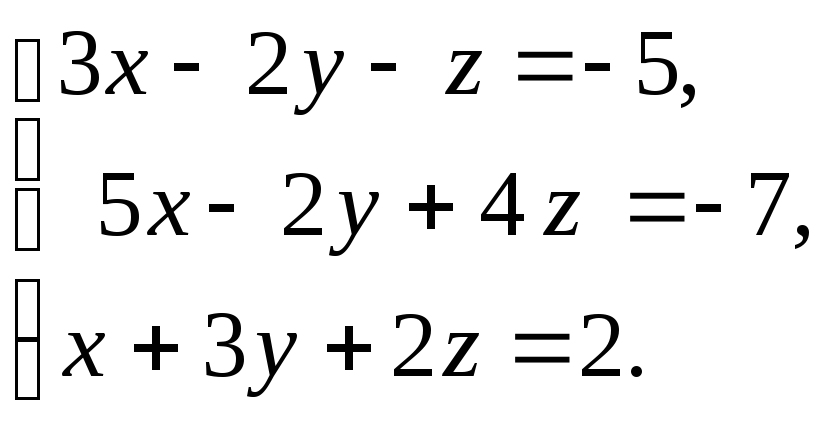 б)
б)

15. а)
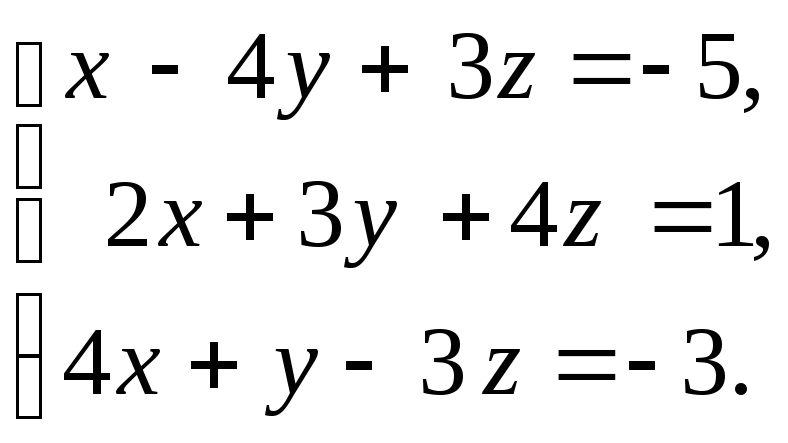 б)
б)
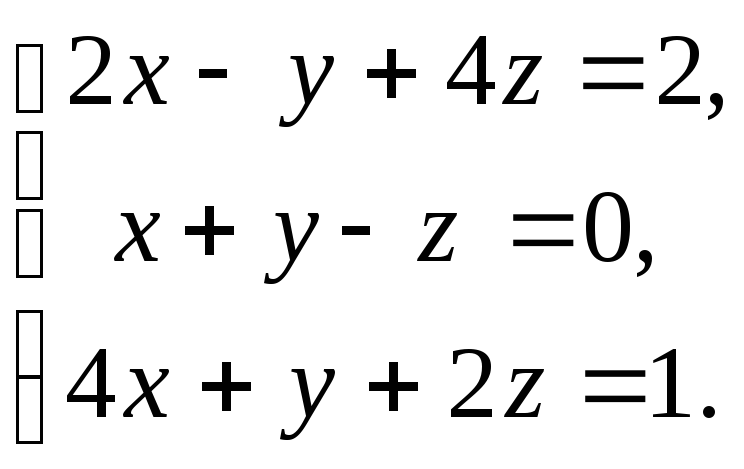
16. а)
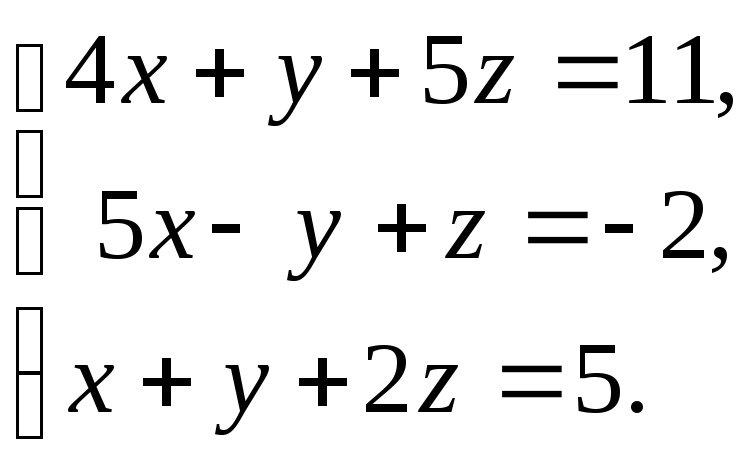 б)
б)
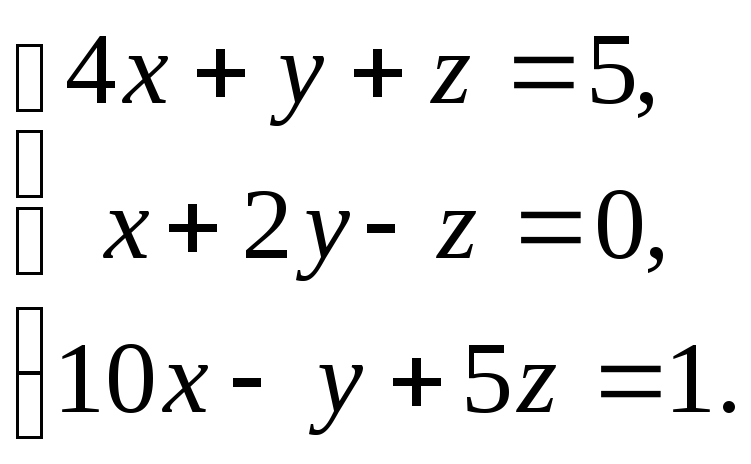
17. а)
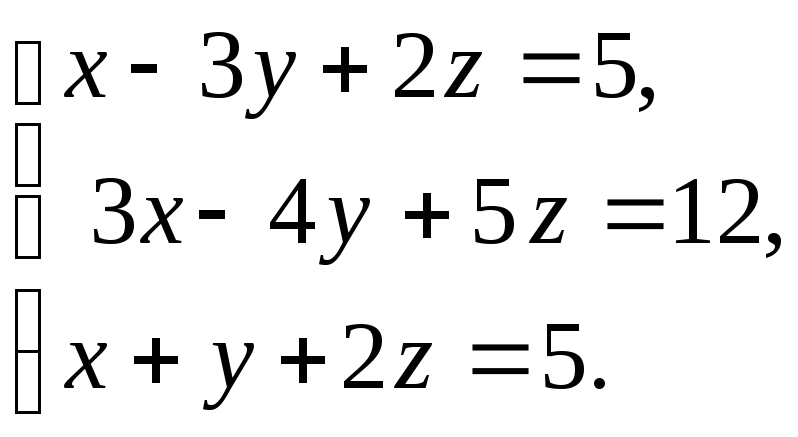 б)
б)

18. а)
 б)
б)
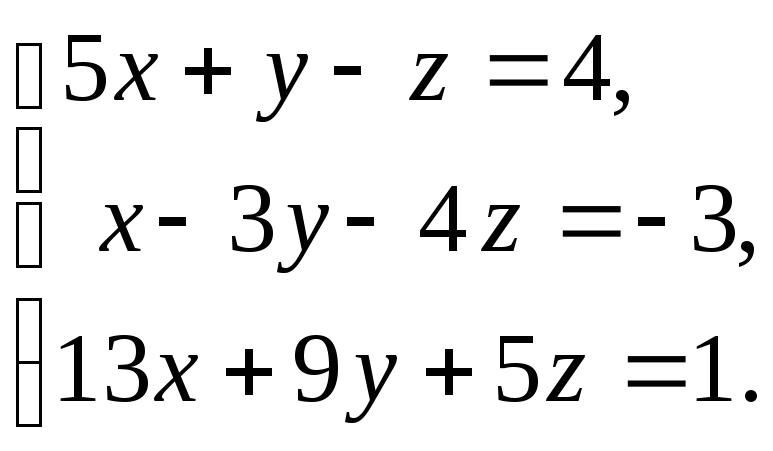
19. а)
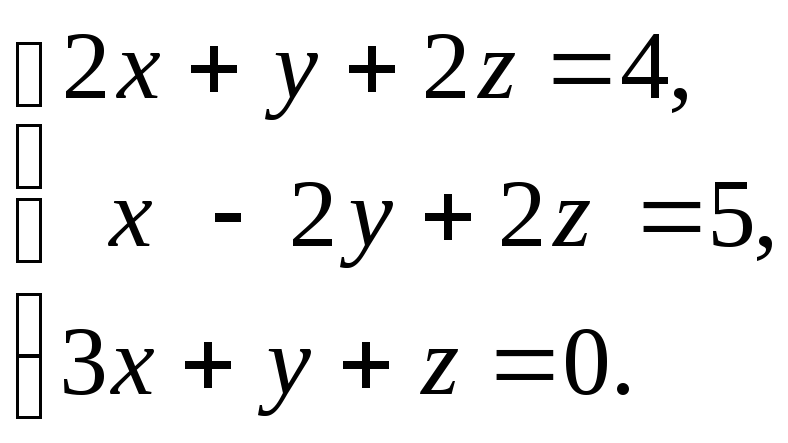 б)
б)
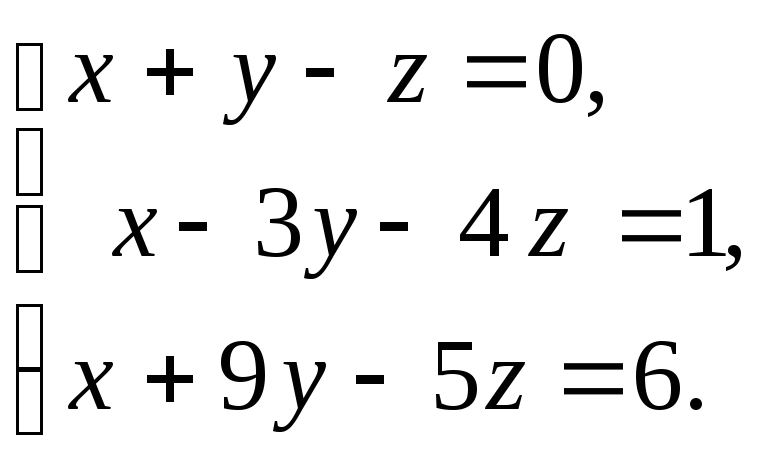
20. а)
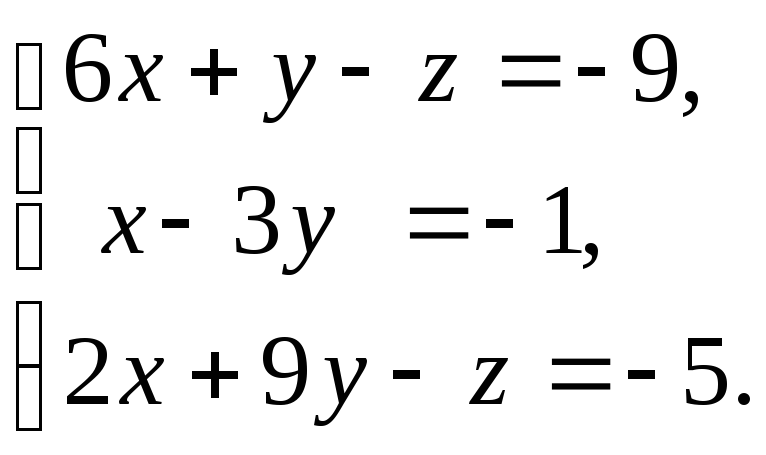 б)
б)

Найти координаты и модуль вектора
 ,
угол между векторами
,
угол между векторами и
и .
Построить на плоскости
.
Построить на плоскости вектор
вектор как заданную алгебраическую сумму,
сравнить результаты аналитического и
графического решений
как заданную алгебраическую сумму,
сравнить результаты аналитического и
графического решений
А(3; 2), В(1; 6), С(3; 8),
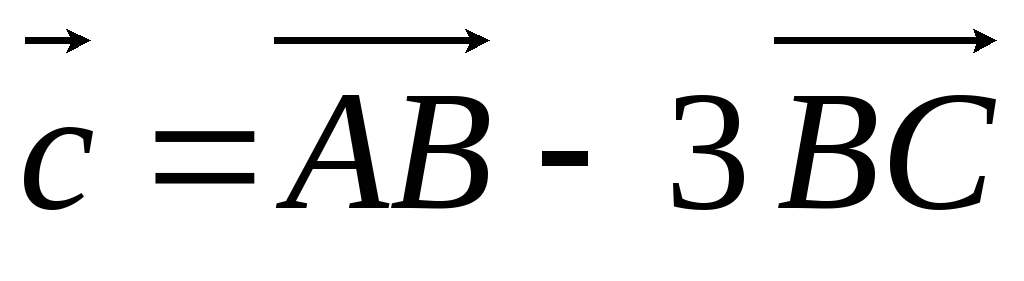 .
.А(–3; 4), В(0; 6), С(1; 8),
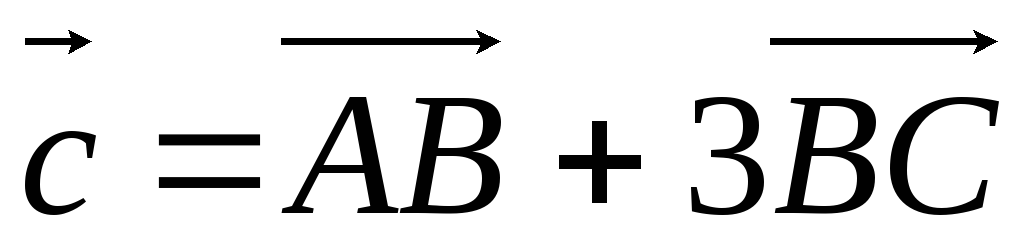 .
.А(1; –2), В(–1; 2), С(1; 4),
 .
.А(–4; –3), В(–1; 5), С(0; 3),
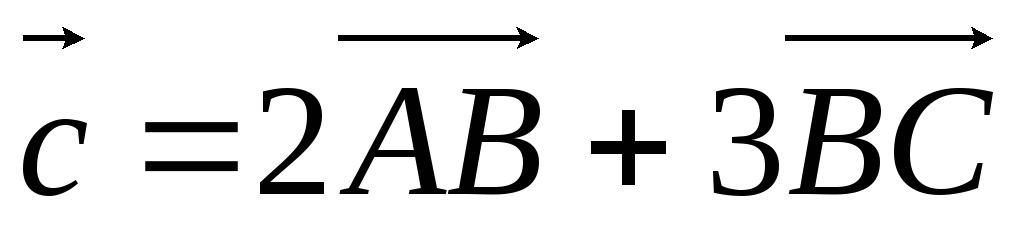 .
.А(3; 2), В(1; 6), С(5; 8),
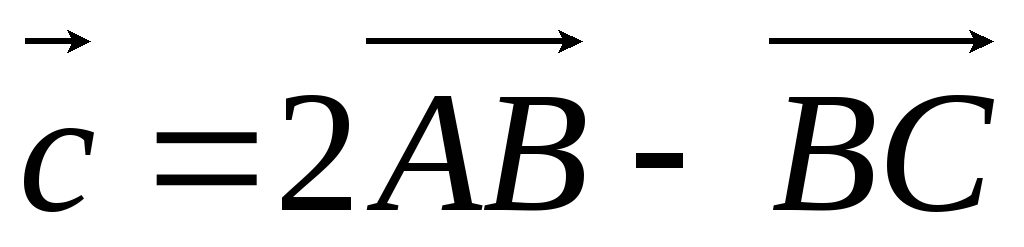 .
.А(–3; 4), В(0; 6), С(1; 4),
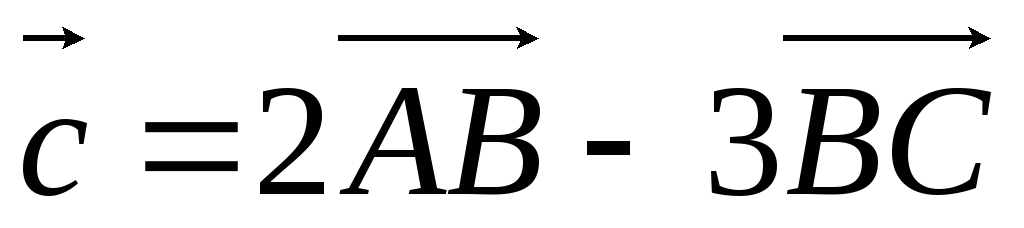 .
.А(1; –2), В(–1; 2), С(1; 4),
 .
.А(–4; 3), В(–1; 6), С(0; 3),
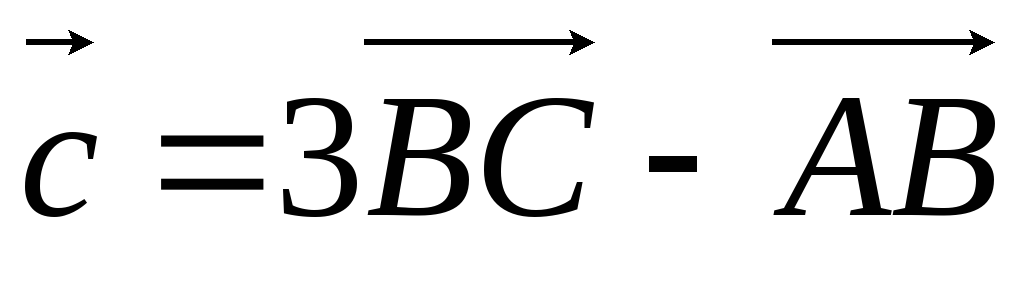 .
.А(1; –2), В(–1; 2), С(1; 4),
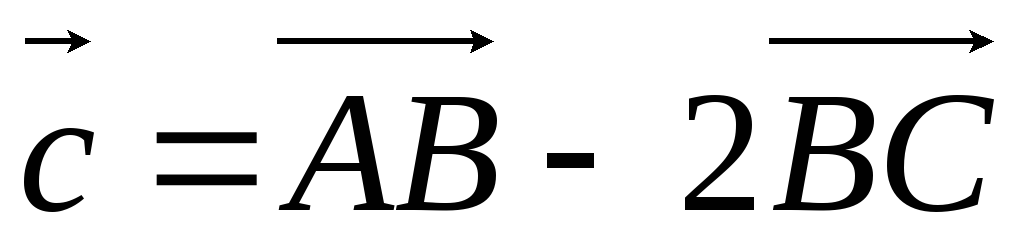 .
.
10) А(–3; 4), В(0;
6), С(1; 4), ![]() .
.
11)
А(2;
–1), В(3;
2), С(4;2) , ![]()
12)
А(3;
0), В(4; 2), С(5;
–1),
![]()
13)
А(2;
4), В(6; 1), С(4; 2), ![]()
14)
А(4;
3), В(6; 4), С(5; 6), ![]()
15)
А(–2;
0), В(2; 3), С(4;
–1), ![]()
16)
А(4;
2), В(6; 2), С(7; 1), ![]()
17)
А(4;
1), В(6; –2), С(4;
–1), ![]()
18)
А(4;
1), В(2; –1), С(1;
2), ![]()
19)
А(2; –1), В(4;
3), С(–2;
0) , ![]()
20)
А(0;
4), В(1; 2), С(4; 3), ![]()
Найти аналитически и графически точку пересечения
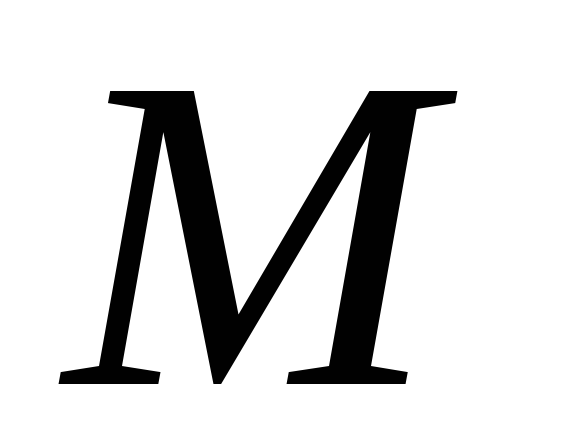 между прямыми
между прямыми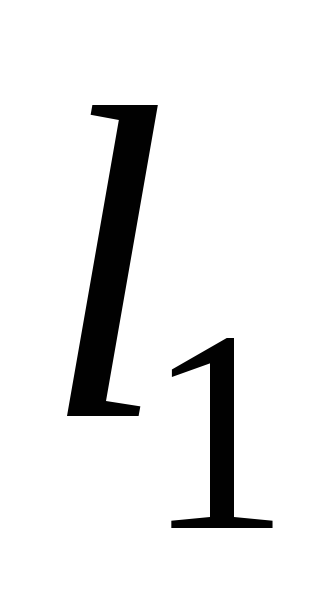 и
и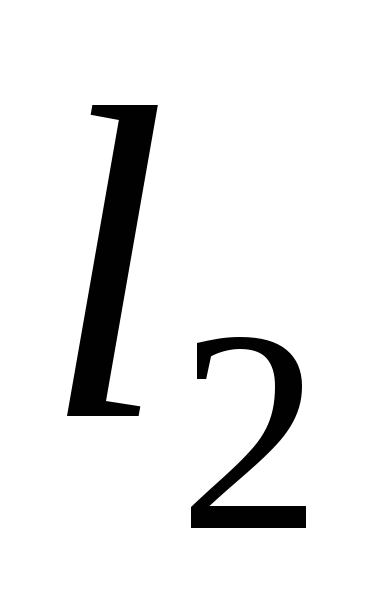 ,
угловые коэффициенты прямых
,
угловые коэффициенты прямых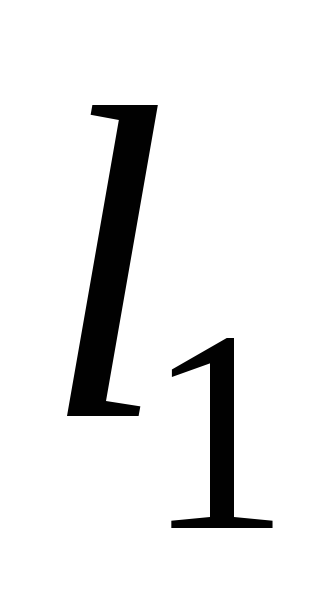 и
и и угол между ними. Проверить аналитически
принадлежит ли точка
и угол между ними. Проверить аналитически
принадлежит ли точка прямой
прямой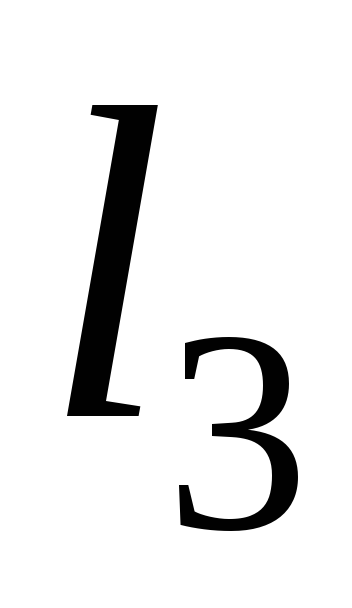 .
Составить уравнение прямой
.
Составить уравнение прямой ,
проходящей через точку
,
проходящей через точку ,
перпендикулярно вектору
,
перпендикулярно вектору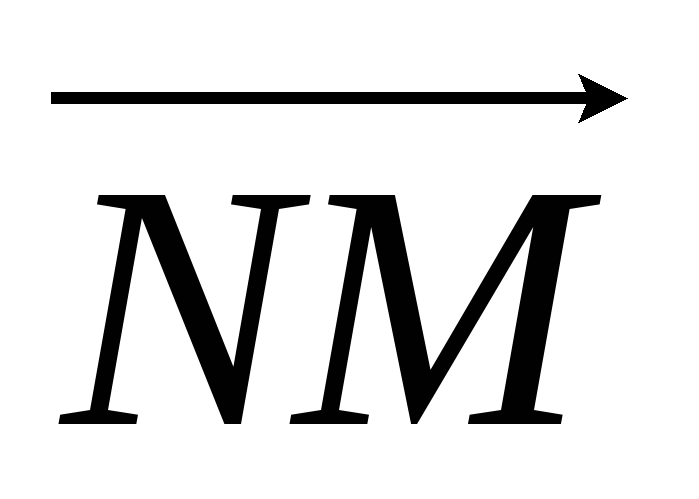 .
Составить уравнение прямой
.
Составить уравнение прямой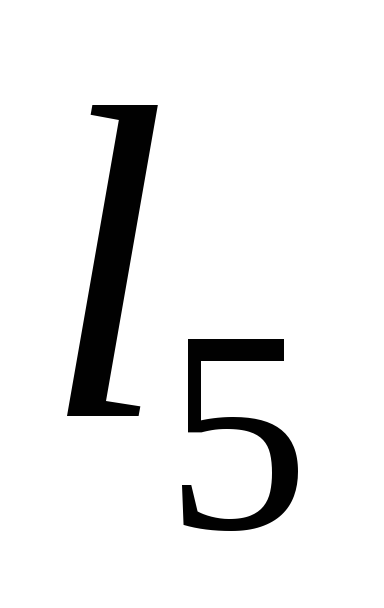 ,
проходящей через точки
,
проходящей через точки и
и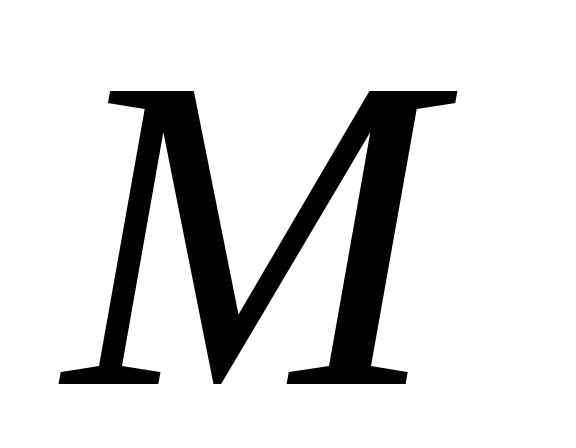 .
Построить все прямые на координатной
плоскости
.
Построить все прямые на координатной
плоскости
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
11)
|
12)
|
|
13)
|
14)
|
15)
|
|
16)
|
17)
|
18)
|
|
19)
|
20)
|
|
Назвать, дать определение, записать каноническое уравнение и построить заданные кривые. Для окружности найти координаты центра и радиус, для остальных кривых найти координаты фокусов
1) а)
![]() 2) а)
2) а)
![]() 3) а)
3) а)
![]()
б)
![]() б)
б)![]() б)
б)![]()
в)
![]() в)
в)![]() в)
в)![]()
г)
![]() г)
г)![]() г)
г)![]()
4)
а)
![]() 5)
а)
5)
а)
![]() 6)
а)
6)
а)
![]()
б)
![]() б)
б)![]() б)
б)![]()
в)
![]() в)
в)![]() в)
в)![]()
г)
![]() г)
г)![]() г)
г)![]()
7)
а)
![]() 8) а)
8) а)
![]() 9)
а)
9)
а)
![]()
б)
![]() б)
б)![]() б)
б)![]()
в)
![]() в)
в)![]() в)
в)![]()
г)
![]() г)
г)![]() г)
г)![]()
10)
а)
![]() 11)
а)
11)
а)
![]() 12)
а)
12)
а)
![]()
б)
![]() б)
б)![]() б)
б)![]()
в)
![]() в)
в)![]() в)
в)![]()
г)
![]() г)
г)![]() г)
г)![]()
13)
а)
![]() 14)
а)
14)
а)
![]() 15)
а)
15)
а)
![]()
б)
![]() б)
б)
![]() б)
б)
![]()
в)
![]() в)
в)![]() в)
в)
![]()
г)
![]() г)
г)
![]() г)
г)![]()
16)
а)
![]() 17)
а)
17)
а)
![]() 18) а)
18) а)
![]()
б)
![]() б)
б)
![]() б)
б)
![]()
в)
![]() в)
в)![]() в)
в)
![]()
г)
![]() г)
г)
![]() г)
г)
![]()
19)
а)
![]() 20)
а)
20)
а)
![]()
б)
![]() б)
б)
![]()
в)
![]() в)
в)
![]()
г)
![]() г)
г)
![]() .
.
Вычислить пределы
1)
![]() при а)
при а)![]() ;
б)
;
б)![]()
2)
![]() при а)
при а)![]() ;
б)
;
б)![]()
3)
![]() при а)
при а)![]() ;
б)
;
б)![]()
4)
![]() при а)
при а)![]() ;
б)
;
б)![]()
5)
![]() при а)
при а)![]() ;
б)
;
б)![]()
6)
![]() при а)
при а)![]() ;
б)
;
б)![]()
7)
![]() при а)
при а)![]() ;
б)
;
б)![]()
8)
![]() при а)
при а)![]() ;
б)
;
б)![]()
9)
![]() при а)
при а)![]() ;
б)
;
б)![]()
10)
![]() при а)
при а)![]() ;
б)
;
б)![]()
11)
![]() при а)
при а)
![]() ;
б)
;
б)![]()
12)
![]() при а)а
= 0;
б)
при а)а
= 0;
б)
![]()
13)
![]() при а)
при а)
![]() ;
б)
;
б)
![]()
14)
![]() при а)а
= 1;
б)
при а)а
= 1;
б)
![]()
15)
![]() ;
при а)а
= –1;
б)
;
при а)а
= –1;
б)
![]()
16)
![]() при
а)
а
= 0;
б)
при
а)
а
= 0;
б)
![]()
17)
![]() при
а)
а
=
0; б)
при
а)
а
=
0; б)
![]()
18)
![]() при а)а
= 3;
б)
при а)а
= 3;
б)
![]()
19)
![]() при а)а
= 2;
б)
при а)а
= 2;
б)
![]()
20)
![]() при а)а
= 2;
б)
при а)а
= 2;
б)
![]()
Найти производные заданных функций:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
2) а)
![]() ;
б)
;
б)![]() ; в)
; в)![]()
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
5) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
6) а)
![]() ; б)
; б)![]() в)
в)![]()
7) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
8) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
9) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
10) а)
![]() ; б)
; б)![]() ; в)
; в)![]()
11)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
12)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
13)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
14)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
15)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
16)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
17)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
18)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
19)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
20)
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
Исследовать функции и построить их графики. Найти наименьшее и наибольшее значение функции на указанном промежутке
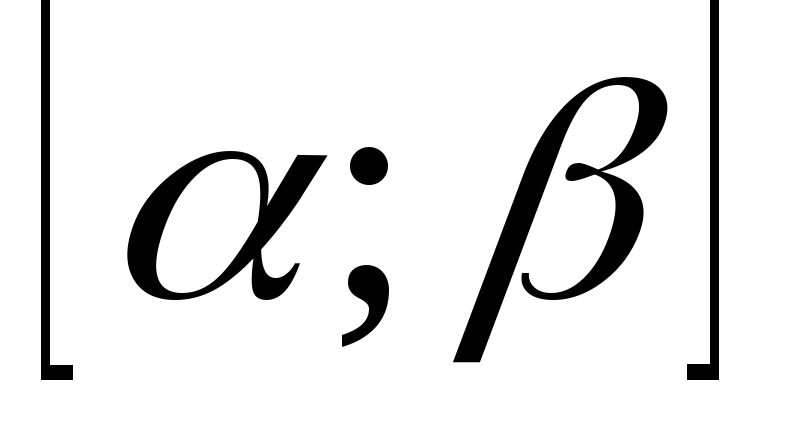
1. a)
![]() ; б)
; б)
![]() .
.
2. a)
![]() ; б)
; б)
![]() .
.
3. a)
![]() ; б)
; б)
![]() .
.
4. a)
![]() ; б)
; б)
![]() .
.
5. a)
![]() ; б)
; б)
![]() .
.
6. a)
![]() ; б)
; б)
![]() .
.
7. a)
![]() ; б)
; б)
![]() .
.
8. a)
![]() ; б)
; б)
![]() .
.
9. a)
![]() ; б)
; б)
![]() .
.
10. a)
![]() ; б)
; б)
![]() .
.
11. a)
![]() ; б)
; б)
![]() .
.
12. a)
![]() ; б)
; б)
![]() .
.
13. a)
![]() ; б)
; б)
![]() .
.
14. a)
![]() ; б)
; б)
![]() .
.
15. a)
![]() ; б)
; б)
![]() .
.
16. a)
![]() ; б)
; б)
![]() .
.
17. a)
![]() ; б)
; б)
![]() .
.
18. a)
![]() ; б)
; б)
![]() .
.
19. a)
![]() ; б)
; б)
![]() .
.
20. a)
![]() ; б)
; б)
![]() .
.
