3.2. Решение ду с помощью преобразования Лапласа

Применение преобразования Лапласа позволяет перейти от решения системы ДУ к решению системы алгебраических уравнений. Кроме того, исключается необходимость определения постоянных интегрирования, т.к. их учитывают при применении преобразования Лапласа, а общее решение неоднородного ДУ при любой правой части определяется сразу, т.е. исключается раздельное нахождение y₁(t) иy₂(t).

Пусть f(t) – действительная функция действительного переменногоt, удовлетворяющая условиям Дирихле (непрерывна и дифференцируема на рассматриваемом интервале) и равная нулю приt< 0. Будем называть эту функциюоригиналом. Каждому оригиналуf(t) всегда можно поставить в соответствие функциюF(p) комплексного переменного, определенную как интеграл вида

(3.4)

или

,

где L– преобразование Лапласа.

Правая часть (3.4) называется прямым преобразованием Лапласафункцииf(t), а функцияF(p) –изображением Лапласа.

В таблице представлены Лапласовы изображения некоторых функций.

Оригинал	Изображение по Лапласу
f(t) = A
f(t) = 1(t)
f(t) = (t)

Приведем основные свойства преобразования Лапласа.

1. Свойство линейности. Изображение алгебраической суммы нескольких функций равно сумме изображений этих функций:

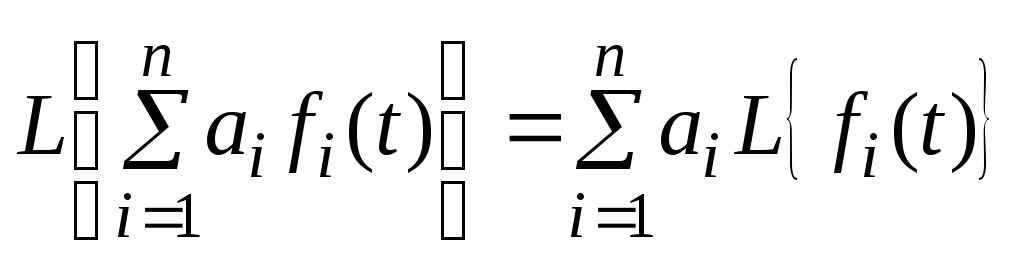. (3.5)

Справедливость выражения (3.5) вытекает из определения (3.4), в соответствии с которым преобразование Лапласа представляет собой линейную операцию.

2. Дифференцирование оригиналов.Производной от функцииf(t) соответствует разность изображений этой функцииF(p), умноженной наp, и ее начального значенияf(0):

. (3.6)

Действительно, умножив (3.4) на p, получим

.

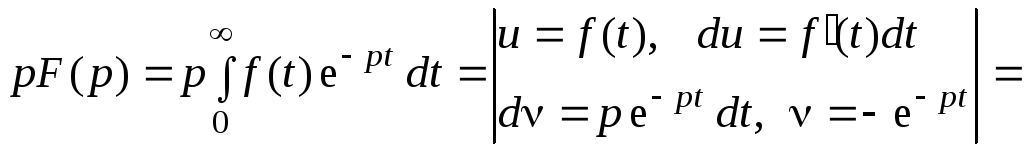
Выполнив этот прием nраз, получим

. (3.7)

Выражение (3.7) является математической записью теоремы дифференцирования. При нулевых начальных условиях выражение (3.7) принимает вид

.

3. Изображение интеграла. Можно показать, что

.

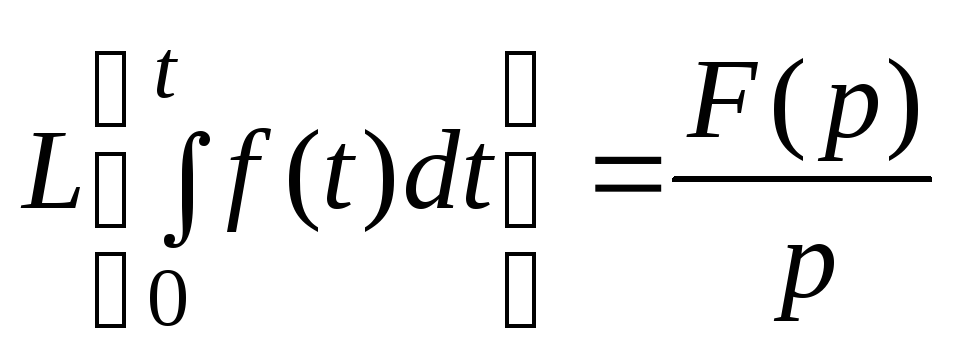Рассмотрим методику интегрирования линейных ДУ с постоянными коэффициентами. В соответствии со свойствами 1 и 2, ДУ в области вещественного переменного tпреобразуются в области комплексного переменногоpв алгебраическое выражение. При этом автоматически учитываются начальные условия и определяются постоянные интегрирования. Имеем

. (3.8)

Умножив (3.8) на после интегрирования его поtв пределах от 0 допри нулевых начальных условиях, получим это уравнение, преобразованное по Лапласу:

.

Отсюда

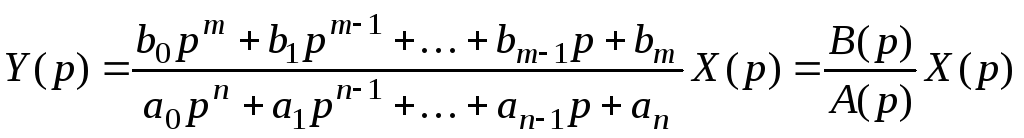. (3.9)

Обозначим . Тогда (3.9) перепишется в видеY(p) = W(p)X(p), откуда

. (3.10)

Выражение (3.10), т.е. отношение изображения выходной переменной системы Y(p) к изображению входной переменнойX(p) при нулевых начальных условиях, называетсяпередаточной функциейсистемы.

Поскольку при исследовании динамических свойств системы требуется определить зависимость переменных в функции действительного аргумента t, возникает обратная задача: как от изображения переменной перейти к ее оригиналу.

Наиболее общим способом нахождения оригинала y(t) по известному изображениюY(p) является применение обратного преобразования Лапласа:

. (3.11)

Для большинства типовых изображений обратное преобразование Лапласа табулировано, поэтому наиболее простым способом нахождения оригинала по изображению является использование таблиц, в которых для наиболее распространенных функций y(t) приведены соответствующие изображенияY(p).

Представим Y(p) дробно-рациональной функцией вида

,

где B(p) иA(p) – полином соответственно m-й иn-й степени, причемm<n.

Тогда оригинал y(t) находим по теореме разложения Хевисайда – Карсона:

, (3.12)

где p_k– корни уравненияA(p) = 0;.

➢   Пример 4. Пусть ДУ системы имеет вид

.

Требуется найти W(p),w(t),h(t).

Преобразуем ДУ системы по Лапласу при нулевых начальных условиях. Получим. Откуда передаточная функция будет

.

Пусть k = 1, a₀ = 1, a₁ = 3, a₂ = 2. Для нахождения функции весаw(t) воспользуемся теоремой разложения. При этом учтем, чтоL{(t)} = 1. Тогда

. (3.13)

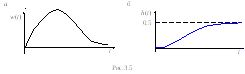
Имеем A(p) = a₀p² + a₁p + a₂ = p² + 3p + 2 = 0; p₁ = –1; p₂ = –2; A(p) = 2p + 3; B(p) = k = 1. Тогда, подставивB(p),A(p),p₁иp₂в выражение (3.13), получим (рис.3.5,а)

.

Аналогичным образом находим переходную характеристику (рис.3.5, б), при этом учитываем, чтоL{1(t)} = 1/р, тогдаA(p) = (p² + 3p + 2)р = 0;p₁ = –1;p₂ = 2;p₃ = 0;A(p) = 3p² + 2р + 2. Воспользовавшись (3.12), найдем

.