5.7. Управляемость и наблюдаемость

Рассмотрим n-мерное пространство состояний, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат().

Пусть в пространстве состояний заданы два множестваи. Рассматриваемая система будетуправляемой, если существует такое управление, определенное наконечном интервале времени , которое переводит изображающую точку в пространствеиз подобластив подобласть.

Можно сузить определение управляемости и понимать под ним возможность перевода изображающей точки из любой области пространства состояний в начало координат, т.е. в точку, соответствующую нулевым отклонениям управляемых координатот заданных значений. Система будетполностью управляемой, если каждое состояние управляемо в этом смысле. Если невозможно подобрать управления, приводящие систему в начало координат ни из одного возможного состояния, система неуправляема.

Система считается наблюдаемой, если в формировании вектора выходных координатучаствуют все составляющие вектора фазовых координат. Если ни одна из составляющих векторане влияет на формирование выхода системы, то такая система ненаблюдаема.

Исходные дифференциальные уравнения многомерной системы управления могут быть представлены в форме Коши в матричной записи:

(5.12)

где – вектор фазовых координат размерности1n(nсоответствует порядку дифференциального уравнения);– вектор управляемых (выходных) величин системы размерности1m;– вектор управляющих величин размерности1k;– вектор возмущающих и задающих воздействий размерности1l;;;;;– соответствующие матрицы коэффициентов.

От пространства состояний перейдем к преобразованному пространству состоянийпосредством преобразования, где– матрица коэффициентов размерности.

Тогда вместо (5.12) будем иметь

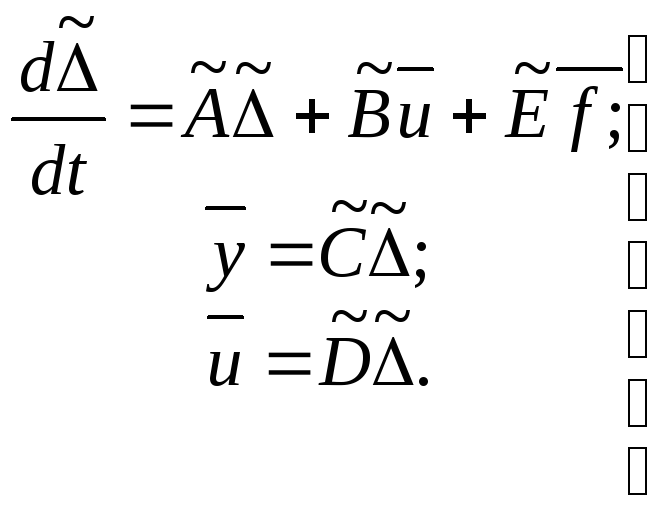(5.13)

Здесь использованы преобразованные матрицы коэффициентов:

;;;;.

Введение новых фазовых координат посредством преобразования приводит к эквивалентным системам различной структуры. При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (5.13) или часть фазовых координат не участвует в формировании выхода. В первом случае система будет не полностью управляемой, во второй – не полностью наблюдаемой.

Р.Калманом были доказаны критерии управляемости и наблюдаемости системы.

Размерность управляемой части системы совпадает с рангом матрицы:

.

При система полностью управляема, при– не полностью управляема, при– неуправляема.

Размерность наблюдаемой части системы совпадает с рангом матрицы:

.

При система полностью наблюдаема, при– не полностью наблюдаема; при– ненаблюдаема.

➢   Пример 11.Рассмотрим систему, изображенную на рис.5.31, а. Количество фазовых координат(они обусловлены наличием в системе емкостей). В отсутствие управляющего сигналауправлениевоздействует только на две фазовые координаты, обусловленные емкостямии(сокращается), т.е., и система не полностью управляема. При подаче сигналапоявляется воздействие и на фазовую координату, система становится полностью управляемой ().

Система, изображенная на рис.5.31, б, не полностью наблюдаема, так как в формировании выходаучаствуют только две фазовые координаты из трех (и). При подаче управляющего сигнала между двумя звеньями системы фазовая координатастановится наблюдаемой, поскольку также участвует в формировании выхода системы.

Таким образом, понятие управляемости системы характеризует способность входа возбуждать все переменные состояния (фазовые координаты) выхода; понятие наблюдаемости – способность состояниясоздавать выходной сигнал.