База непериодического сигнала

База сигнала – это один из важнейших параметров сигнала:

Произведение ширины спектра на длительность сигнала – это постоянная величина. В зависимости от величины B все сигналы делят на две группы:

1) Если база сигнала близка к единице, то такие сигналы называют простейшими.

2) Если база сигнала значительно больше единицы, то такие сигналы называют сложными.

Соотношение между длительностью сигнала и шириной его спектра

- const.

Отсюда

,

т. е. полоса спектра сигнала изменяется обратно пропорционально его длительности. Это значит, что, чем протяженнее сигнал во времени, тем уже его спектр, и наоборот, чем короче сигнал, тем шире его спектр.

Соотношение между спектром одиночного импульса и спектром периодической последовательности импульсов

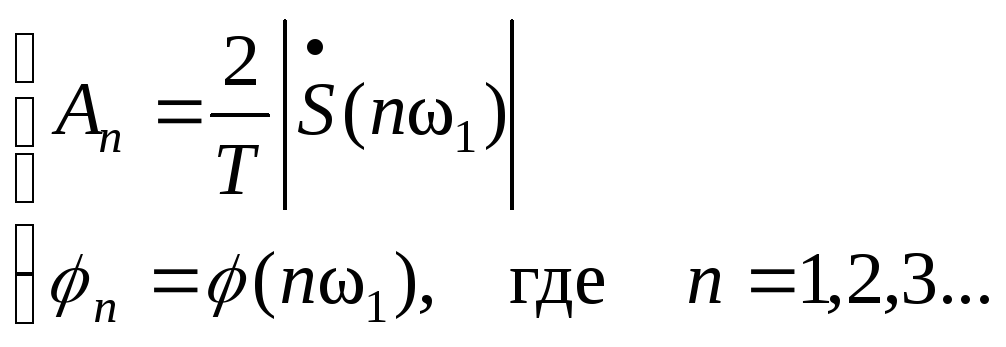
-значение спектральной плотности одиночного импульса на частоте , гдеnω₁ – частоты гармоник. Эти функции практически используются для определения спектров периодических сигналов. Последовательность действий при определении спектра периодического сигнала по спектру одиночного импульса:

1. Определить спектральную плотность центрального одиночного импульса.

2. Записать формулу амплитудного спектра путем подставления в эту формулу вместо частоты ω частоту nω₁, и по формуле вычислить амплитудный спектр периодической последовательности импульсов.

3. В формулу фазового спектра одиночного импульса вместо текущей частоты ω подставить текущую частоту nω1, и по формуле

вычислить фазовый спектр периодической последовательности импульсов.

ВЫВОД. Непрерывный амплитудный спектр одиночного импульса является огибающей дискретного амплитудного спектра периодической последовательности импульсов. Непрерывный фазовый спектр одиночного импульса является огибающей дискретного фазового спектра периодической последовательности импульсов.

Продемонстрируем все вышесказанное на примере. В качестве сигнала возьмем импульсы:

, найдем амплитудный спектр периодической последовательности прямоугольных импульсов:

, n=1,2,3…

; ,, , .

Форма фазового спектра

Связь между преобразованием сигналов и спектров

Запись означает, что сигнал и его спектр однозначно связаны преобразованиями Фурье. В математике известны свойства преобразования Фурье. На основании этих свойств можно установить соответствие между преобразованиями сигналов и соответствующими преобразованиями их спектров. На основании свойств преобразований Фурье можно:

вычислять спектры сложных сигналов,

установить, как изменится спектр, если изменится каким-либо образом сигнал.

Первое свойство - свойство линейности.

,

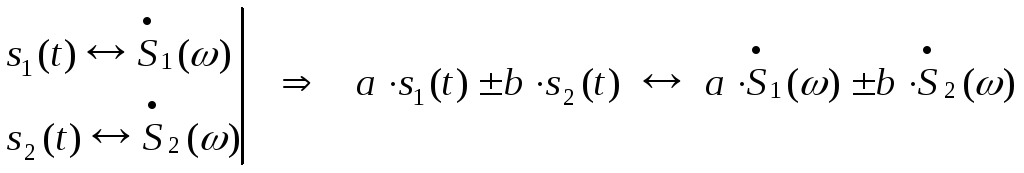где a и b – это некоторые постоянные.

Например:

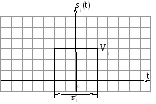
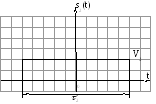
Результат сложения этих двух сигналов:

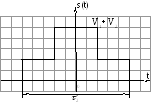
Спектр сигналов:

, .

Спектр результирующего сигнала:

.

Второе свойство - смещение сигнала во времени.

при смещении во времени:

, .

При смещении сигнала во времени его амплитудный спектр не изменяется. Изменяется только фазовый спектр.

Например:

,

.

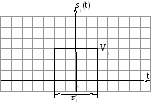
Амплитудный спектр не изменяется, фазовый спектр изменяется:

.

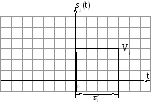Третье свойство - изменение временного масштаба сигнала a>0:

.

При изменении временного масштаба происходит обратное изменение частотного масштаба. При сжатии сигнала во времени его спектр расширяется, а при растягивании сигнала его спектр сужается:

.

Четвертое свойство - смещение сигнала по частоте:

.

Пятое свойство - дифференцирование сигнала:

,

.

Шестое свойство - интегрирование сигнала

.