Воздействие гауссовского процесса на элемент с

симметричной квадратичной характеристикой

Полагаем у=ах².

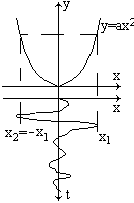
Дифференцируя dy/dx=2ах, и учитывая, что каждому значению у соответствует 2 значения х (), найдем:

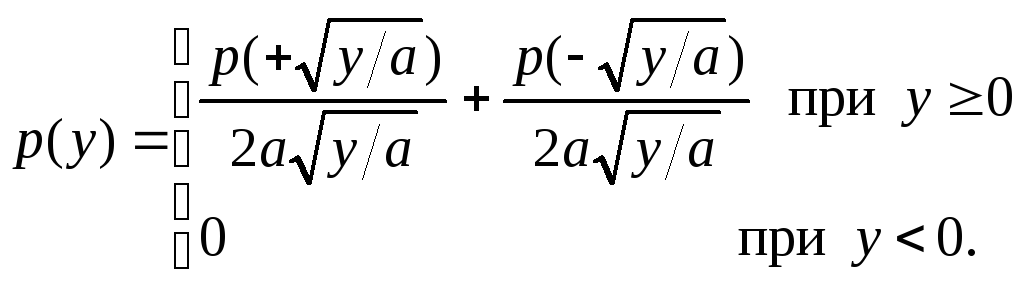
Подставляя данные в выражение, получим

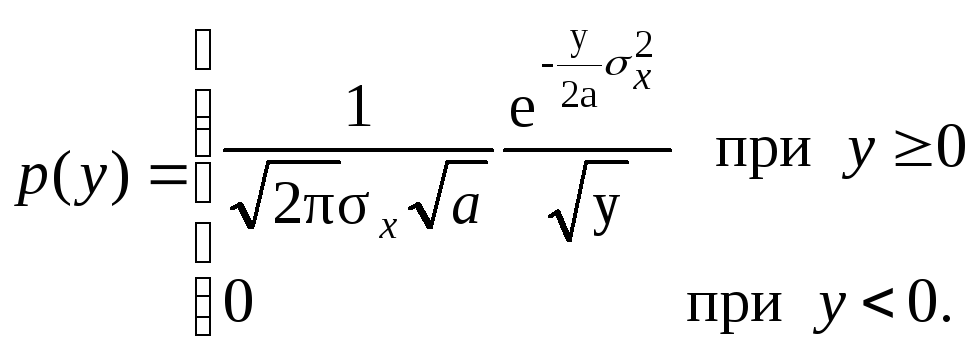
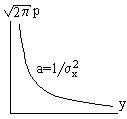
Воздействие нормально распределенного процесса на

однополупериодный детектор с линейно ломаной

характеристикой

В данном случае

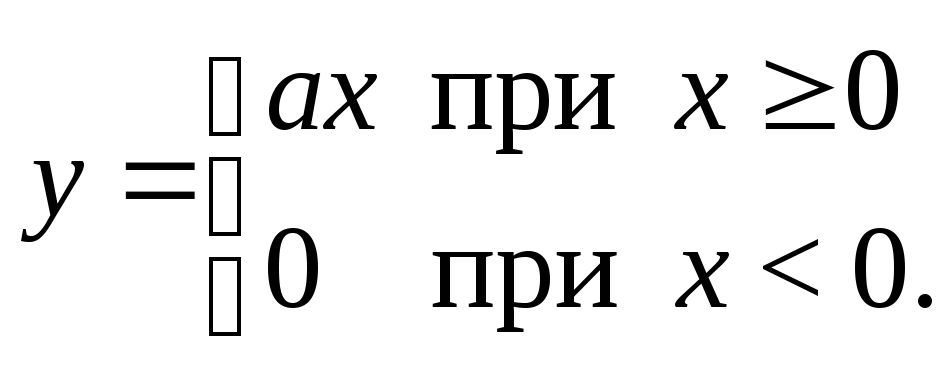
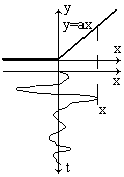
Плотность распределения вероятности в этом случае:

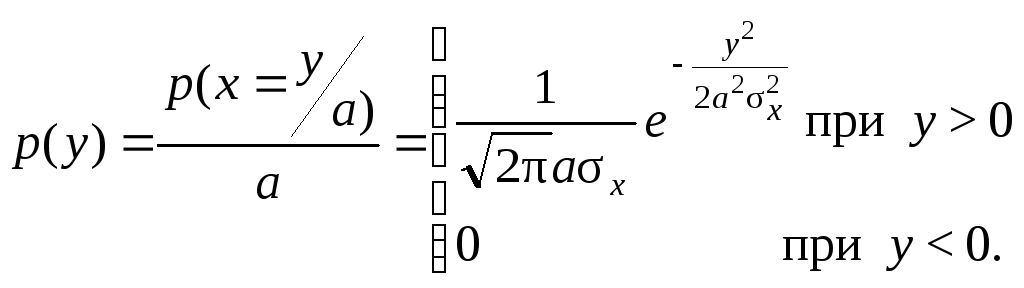
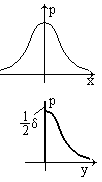
Плотность вероятности р(у=0)=, так как у=0 при х меньше 0. Это можно учесть, записав следующее выражение для р(у):

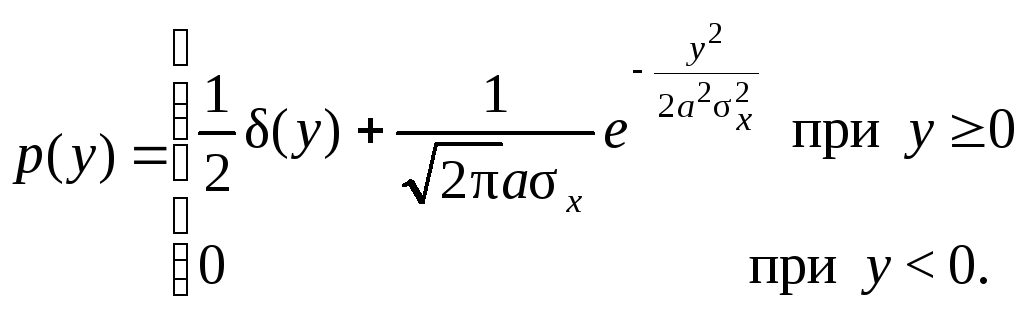
Первое слагаемое будет всюду равно 0, кроме точки у=0, где оно обращается в бесконечность. При интегрировании же по у это слагаемое дает 1/2.

Воздействие нормально распределенного

процесса на ограничитель

По аналогии с предыдущим случаем составим выражение

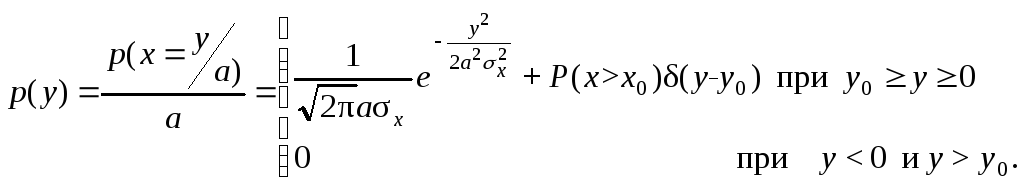
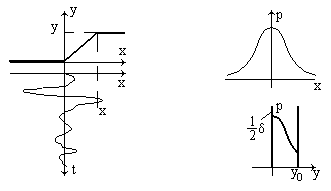
Преобразование спектра случайного процесса

в безынерционном нелинейном элементе

Непосредственно по формулам определить спектр на выходе по известному спектру на входе невозможно, нужно сначала найти корреляционную функцию на выходе и применить прямое преобразование Фурье.

Если на выходе есть нелинейная функция, то можно найти ее ковариационную функцию:

.

Если известна двумерная плотность вероятности входного процесса, то

.

Этот интеграл довольно трудно вычислять, поэтому прибегают к различным упрощениям.

Пример. Пусть у=ах². Двумерная плотность вероятности процесса x(t) равна

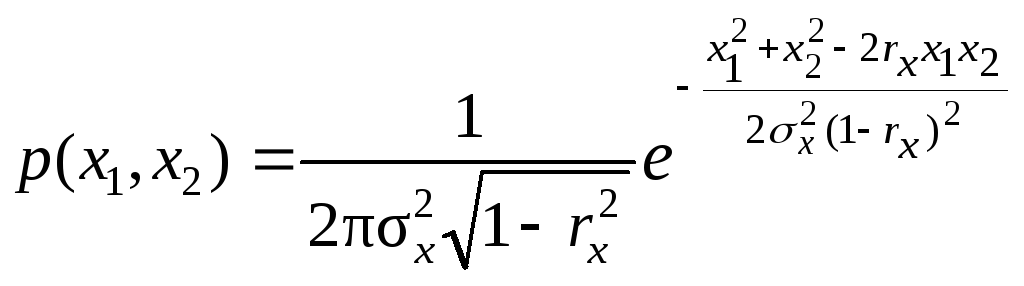, где r_x=r_x() – нормированная корреляционная функция входного процесса.

Проделав необходимые преобразования и использовав соотношение

,

перейдем к выражению

.

Пусть x(t) - узкополосный процесс, тогда, учитывая, что ,

где r₀ – огибающая корреляционной функции узкополосного процесса, запишем окончательное выражение:

.

Применим теперь прямое преобразование Фурье и получим выражение для энергетического спектра процесса на выходе элемента:

Первое слагаемое (дискретное) соответствует постоянной составляющей выходного колебания, второе – низкочастотной составляющей, спектр которой примыкает к нулевой частоте, третье – высокочастотной составляющей со спектром, группирующимся вблизи частоты 2₀.

ВЫВОД. Спектр на выходе существенно отличается от спектра на входе и имеет 3 составляющие.

Воздействие узкополосного шума на амплитудный детектор

Амплитудный детектор, содержащий диод и фильтр нижних частот (RC-цепь), представляет собой сочетание безынерционного нелинейного элемента с инерционной линейной цепью.

Линейное детектирование. Детектирование высокочастотного колебания с большой амплитудой.

Считаем, что напряжение на выходе детектора воспроизводит амплитуду колебания на входе, т. е. считаем, что коэффициент передачи детектора равен 1. Таким образом, напряжение шума на выходе линейного детектора обладает релеевским распределением:

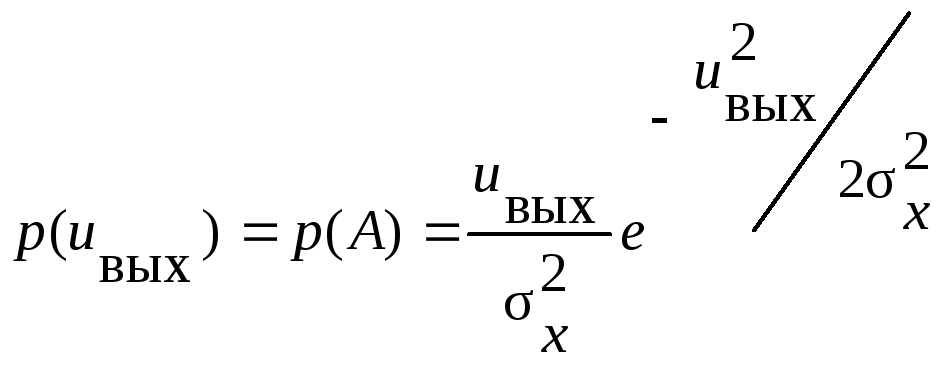при .

Среднее значение шумового напряжения

.

Дисперсия

.

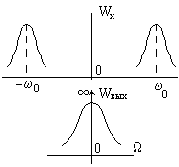
Найдем корреляционную функцию и энергетический спектр выходного сигнала при условии, что на входе линейного детектора действует нормальный шум, энергетический спектр которого

,

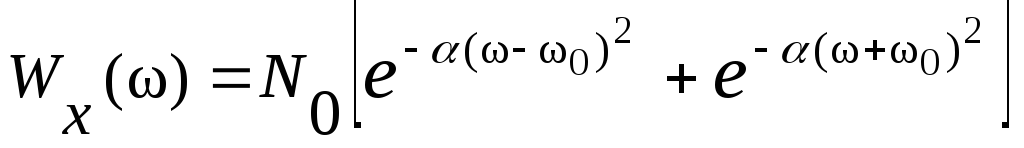а корреляционная функция

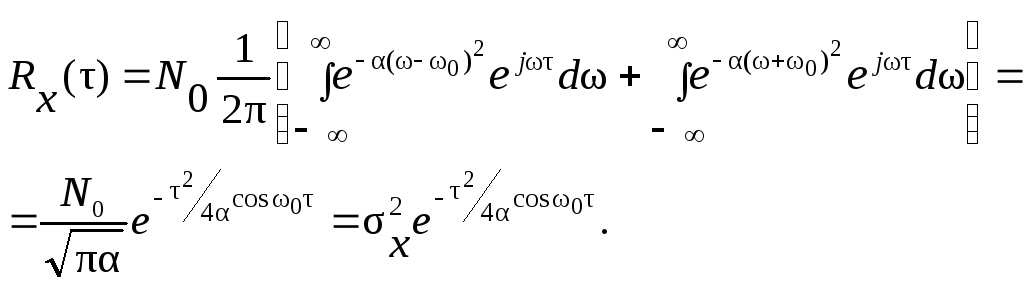
Окончательно получим

.

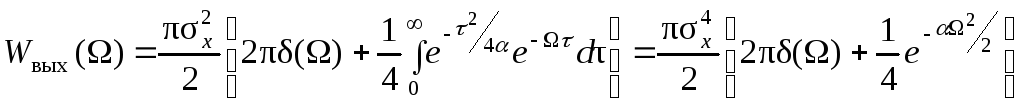ВЫВОД. Ширина выходного спектра в раз больше ширины входного спектра. Линейный амплитудный детектор воспроизводит огибающую узкополосного колебания, независимо от особенностей структуры его спектра, т. е. огибающая каждой реализации шума на выходе детектора обладает спектром более широким, чем частотная полоса самой реализации.