Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет инженерных технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебник мануалов ВГУ по дискретке

.pdf

Скачиваний:

Добавлен:

02.04.2015

Размер:

785.19 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Министерство образования Российской Федерации

Воронежский государственный университет

Факультет прикладной математики и механики Кафедра математических методов исследования операций

Методические указания для решения задач по курсу «Дискретная математика»

для студентов 1 курса дневного и вечернего отделений факультета ПММ

Составители: Азарнова Т.В. Булгакова И.Н.

Воронеж-2000

Азарнова Т.В., Булгакова И.Н. Методические указания для решения задач по курсу Дискретная математика для студентов 1 курса дневного и вечернего отделений факультета ПММ – Воронеж: Лаб. опер. полиг. ВГУ, 2000. – 50 с.

Данная работа содержит краткое изложение теории множеств, бинарных отношений и комбинаторики, соответствующее курсу лекций по дисциплине Дискретная математика, читаемому на факультете ПММ. Пособие содержит ряд примеров, демонстрирующих использование изложенной теории для решения конкретных задач. Для закрепления материала в конце параграфов приведены задачи для самостоятельного решения, которые могут быть также использованы для проведения практических занятий.

Рецензент: кандидат физико-математических наук, доцент Воронежского государственного университета факультета Прикладной математики и механики Кацаран Т.К.

Теория множеств

§1. Элементы теории множеств

Под

множеством

понимается

совокупность

некоторых

объектов

(элементов), объединенных некоторым признаком.

Множества

обычно

обозначают

большими

буквами алфавита Α , Β , Χ

,Υ , Ζ

, Ω .

Элементы,

входящие в множество обозначаются малыми буквами a, b, x, y, z,ω

. Запись

означает, что

является

элементом множества

запись

означает, что x

не принадлежит множеству

Χ .

Два

множества

считаются равными, если они состоят из одних и тех же элементов.

Для описания множества пользуются двумя способами. Первый способ

состоит в простом перечислении его элементов. Так, запись Α = {0,1,5}

означает,

что множество

Α состоит из трех чисел 0,1 и 5. Второй способ

состоит

определении

множества

с помощью некоторого

свойства P,

позволяющего определить, принадлежит ли данный элемент данному

множеству или нет. В этом случае используется коллективизирующее

обозначение

Α = {x : P( x)} ,

которое читается следующим образом:

множество Α

состоит из всех

элементов x , для которых P( x) истинно. Если

свойство

относится к

элементам

некоторого

множества

то

будем

писать

также

{x Χ

: P( x)} . Например, множество

{1,2,3,4,5}

можно задать следующим

образом:

{1,2,3,4,5}

= {x : x −

целое

число

из интервала [1,5}] .

Множество, не содержащее элементов, называется пустым множеством

и обозначается .

Знаком

обозначим отношение включения между множествами, т.е.

, если каждый элемент множества Α

есть элемент множества Β

. Если

, то говорят, что множество Α

есть подмножество множества Β .

Равенство

двух

множеств

означает

выполнение

двух

включений: Α

и Β

Α .

Если

≠

, то

говорят,

что

есть

собственное

подмножество Β

и пишут Α

Β .

называется множеством-

Множество всех подмножеств множества Α

степенью и обозначается Ρ

(Α

) .

Заметим, что: a)

; б) если Χ

, Υ

Ζ , то Χ

Ζ ; в) если

Υ , Υ

, то Χ

= Υ .

Не надо смешивать отношения принадлежности и включения. Хотя 1 {1} , {}1 {}{ 1} , не верно, что 1 {{1}} , так как единственным элементом

множества {{1}} является {1} .

Пустое множество есть подмножество любого множества.

Теория множеств

Число элементов в множестве Χ

обозначается

Рассмотрим методы получения новых множеств из уже существующих.

Объединением множеств Α

называется множество Α Β , все

элементы которого являются элементами множества

или Β :

Α Β

= { x : x

или x

Β }

Α ∩

Пересечением множеств

называется

множество

Β ,

элементы которого являются элементами и множества Α

, и множества Β

Α ∩ Β =

{ x : x Α и x Β

} .

Очевидно, что выполняются включения

Α ∩ Β Α Α Β

и Α ∩ Β Β Α Β .

\ Β

тех

Разностью множеств

называется

множество

элементов из Α , которые не принадлежат Β

Α \ Β =

{ x : x Α и x Β } .

Симметричной разностью множеств Α

и Β

называется множество

Α + Β = Α \ Β Β \ Α .

Если все рассматриваемые в данный момент множества являются

подмножествами некоторого множества U , то

множество U

называют

универсальным для данного рассмотрения.

Дополнением множества Α

называется множество

U \ Α .

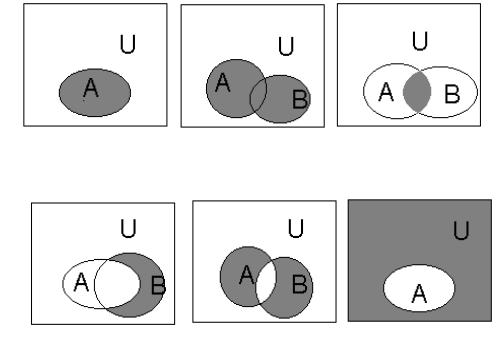
Для наглядного представления

отношений между подмножествами

какого-либо универсального множества используются диаграммы ЭйлераВенна.

Α Β

Α ∩ Β

Β \ Α

Α + Β

Теория множеств

Операции над множествами имеют следующие приоритеты в порядке убывания: операция взятия дополнения, операция пересечения, операция объединения.

Отметим следующие основные законы для операций над множествами:

( коммутативность объединения);

∩

)

(коммутативность пересечения);

(

= ( Α

Β )

(ассоциативность объединения);

∩

(

∩

)

= ( Α

∩

Β )

∩

(

(ассоциативность пересечения);

(

∩

)

= ( Α

Β )

∩

)

(1-й закон дистрибутивности);

∩

(

)

= ( Α

∩

Β )

(

∩

)

(2-й закон дистрибутивности);

;

U =

U ;

∩

;

10. Α

∩

U =

;

11. Α

∩

( закон де Моргана);

12.

( закон де Моргана);

∩

13. Α

(

∩

) =

(закон поглощения);

14. Α

∩

(

) =

(закон поглощения).

Рассмотрим методику решения задач по данной теме.

Задача 1. Равны ли следующие множества:
1)	{2,4,5}	и {2,4,5,2} ;
2)	{1,2} и {{1,2}} ;
3)	{1,2,3}	и {{1} {, }2{ }, 3} ;
4)	{{1,2} ,3}	и {{1} {, 2},3} .

Решение. Для доказательства равенства произвольных множеств нужно проверить, что первое множество включено во второе, а второе, в свою очередь, включено в первое, т.е. любой элемент первого множества является элементом второго множества, а любой элемент второго множества является элементом первого множества.

Проверка дает положительный результат для множеств из пункта 1). Это можно наглядно показать на следующей схеме, где стрелочка, идущая от элемента, показывает, какой элемент в другом множестве ему соответствует.

{2,4, 5}	{2, 4,	5, 2}


{2, 4, 5,2}	{2, 4,	5}

Теория множеств

Множества из пункта 2) неравны, так как, например, элемент 1из первого множества не имеет себе равного во втором множестве. Второе множество состоит из единственного элемента – множества {1,2} .

Множества, указанные в пункте 3) неравны, так как элементами первого множества являются числа 1,2,3, а элементами второго множества являются множества, состоящие из одного элемента {1} {, }2{ }, 3 .

Пункт 4) сделайте самостоятельно.

	Задача 2. Следующие множества заданы перечислением своих
элементов, задайте эти множества				с помощью характерного для их
элементов свойства.
1)	Α =	{2,4,6,8,...,32} ;
		Киев, Минск, Кишинев,Таллинн, Вильнюс, Рига, Москва,
2)	Κ =		Ереван,Тбилиси, Баку,Ташкент, Ашхабад, Душанбе,

			Алма − Ата,Фрунзе

Решение. Множество Α представляет собой множество четных

натуральных чисел от 1 до 32, поэтому это множество можно записать в виде

Α =

{ x Ν

: x = 2n, n = 1,...,16} .

Множество

Κ представляет

собой

множество

столиц республик

бывшего СССР, т.е. это множество можно записать в виде

Κ = { x : x − столица республики

СССР} .

Задача 3. Приведите примеры таких множеств Α

, Β

, Κ , для которых

1) Α Β ,

Β Κ ,

Α Κ ;

2) Α Β , Β Κ , Α Κ ;

3) Α Β , Β Κ , Α Κ ;

4) Α Β ,

Β Κ ,

Α Κ .

Решение. В качестве примера множеств, удовлетворяющих условию из

пункта 1, можно рассмотреть следующие множества

Α = {1,2} , Β = {{ 1},2 ,1} , Κ = {3,{{

1},2 ,1}} .

Пункту 3) удовлетворяют множества

Κ ={

2,3},4 .

= {2,3} ,

Β = {}

1{ , }2,3} ,

Пункты 2) и 4) рассмотрите самостоятельно.

Задача 4. Докажите следующие тождества:

1) Α \ Β = Α

∩

;

Β ) ∩ (Α

) ;

2) Α (Β \ Κ ) = ( Α

3) (Α

Β ) ∩

(

)

= Α ;

4) Β ∩

(Α \ Β

) =

;

5) Α ∩

(Β + Κ ) = (

Α ∩ Β ) + ( Α ∩ Κ) .

Теория множеств

Решение. Для доказательства равенства 1) докажем два включения:

\ Β

∩

\ Β .

Доказательство первого включения проведем по схеме

x Α ∩ Β ,

x Α

\ Β

а доказательство второго включения по схеме

x Α \ Β .

x Α

∩ Β

Заметим, что в данном примере мы могли рассмотреть не две схемы, а одну, но вместо знака следствия использовать знак равносильности .

Тождество 2 можно также доказать с помощью двух включений, но можно и не использовать данную схему, а опираться на уже доказанное тождество 1) и на основные законы 1-14. Мы приведем данный способ доказательства, причем вверху над равенствами будем писать либо 1) – это

означает, что используется тождество 1), либо номер используемого основного закона. Итак,

Α (Β \ Κ ) = 1) Α (Β ∩ Κ ) = 5) (Α Β ) ∩ (Α Κ ) .

Аналогично можно доказать равенства 3),4),5). Для равенства 4)

приведем еще один способ доказательства – доказательство от противного.

Предположим противное, что множество Β

∩

(Α

/ Β

)

не

пусто,

т.е.

существует хотя бы один элемент

Β ∩ (Α \ Β )

x Α .

\ Β

Никакой элемент x не может одновременно

принадлежать и

самому

множеству и его дополнению, поэтому мы пришли к противоречию.

Задача 5. Пусть Α , Β , Κ - такие множества, что Β

Κ . Найдите

множество Χ

, удовлетворяющее системе уравнений

∩

поэтому

Решение. Из первого уравнения следует,

что

можно представить в виде Χ

′

. Из равенств

, где Χ

∩

Α ∩ Χ

= Β ,

= Β Χ ′,

Χ ′∩ Β =

следует, что Α

∩

′

найти множество Χ

′

Заменим Χ

Итак, нам осталось

во

втором

уравнении на Χ

= Β

′

(Β

′

Κ . По ассоциативному

. Получим Α

)

закону (Α

)

′

Κ .

Из включения

следует,

что Α

Β =

Α ,

поэтому

получаем

равносильное

уравнение

′

Два

факта

= Κ .

Теория множеств							8
Теория множеств
Α ∩ Χ	′	и Α	Κ	позволяют			заключить,			что решением	последнего
Α ∩ Χ	=	и Α	Κ	позволяют			заключить,			что решением	последнего
уравнения является множество Χ						′	Κ	\ Α . Окончательно
уравнения является множество Χ						=	Κ	\ Α . Окончательно
				Χ		= Β		(K \ Α	) .
	Задача 6. Докажите, что					условие Α			Β	равносильно	каждому из
следующих условий:				1) Α ∩ Β = Α ;				2) Α Β = Β .
				1) Α ∩ Β = Α ;				2) Α Β = Β .
	Решение. Докажем, что Α					Β	равносильно условию 1).
Итак,	пусть	Α	Β ,	докажем		равенство			Α ∩	Β = Α . Равенство будем
доказывать в два включения. Пусть
Обратно, пусть				x	Α	∩	Β	x	Α .
Обратно, пусть			x Α Α Β		x Α ,			x Β x Α ∩ Β .
			x Α Α Β		x Α ,			x Β x Α ∩ Β .

Теперь предположим, что выполнено условие 1), докажем, что Α Β . Рассмотрим

x Α Α ∩ Β = Α

x Α ∩ Β x Β .

Равносильность

условия

условию 1) мы доказали,

равносильность условию 2) докажите самостоятельно.

Задача 7. Докажите для произвольных множеств Α , Β

, Κ :

если Α

и Α

∩

Κ =

, то Α

Κ ;

если Β

∩

Κ =

и Α ∩

Κ ≠

, то Α

\ Β

≠

Решение.1) Нам нужно доказать, что существует хотя бы один элемент

′

такой, что

′

Κ .

Нам известно, что

Α Β

поэтому

, x

существует некоторый элемент x*

и x* Β

. В силу условия Α

∩

Κ = ,

данный элемент x* Κ . Таким образом,

Κ , x* Β

Κ .

2)Нам нужно доказать, что существует хотя бы один элемент в

множестве Α

\ Β .

Известно,

что

∩

≠

поэтому существует элемент

Α ,

Κ ,

причем, в

силу

условия

Β ∩

Κ = ,

данный

элемент

Β . Итак, мы построили элемент x*

и x*

Β .

Задача 8. Докажите, что для

произвольных

множеств Α , Β

справедливо равенство Ρ

(Α ∩

Β ) =

( Α

) ∩

Ρ(

Β ) .

Решение. Доказательство проведем в виде двух включений, объединив

их одной записью. Пусть

Ρ (Α ∩ Β

) Χ

Α ∩ Β Χ

Α ,

Ρ (Α ),

Ρ ( Β ) Χ

Ρ ( Α) ∩ Ρ( Β) .

Задачи для самостоятельного решения

1.Каждое из следующих множеств задайте в виде некоторого интервала числовой прямой:

Теория множеств

{x R : y R x2 + y 2 = 1} ;

y +

x R : y R x =

;

y2 +

{a R : x R 3x2 + 2ax + a < 0}.

2. Вставьте между множествами символ или так, чтобы получилось

истинное утверждение.

{1}

{1{, 1},2} ;

2){1,2}

{1,2{,}1{ }, 2} ;

{1,2}

{1,2{, 1},2} ;

{1,2,{}1{, }

} ;

{

}

;

{{ }} .

3.Перечислите элементы каждого из следующих множеств:

{ x : x

{}1}

;

{ x : x

{1,2,3}} ;

{ x : x

} .

4. Докажите следующие тождества:

1) (

Α \ Β

)

(

∩

)

= Α ;

Α ∩ Β

Α ∩

(

);

(

Α Β

)

Α ∩ Β

)

= Α + Β ;

(Α \ Β

)

(

)

= (Α Β )

\( Α ∩ Β

) ;

(Α \

)

(

\ Β

)

(Β

)

∩ (Α

);

Α \ (Α

\ Β ) =

Α ∩ Β ;

(Α

\ Β

)

= Α Β ;

(

Α + Β

) + Κ = Α +

( Β + Κ) ;

5. Считая Λ

универсальным множеством для данного рассмотрения,

найдите множество Χ

, удовлетворяющее следующим условиям:

1) Α \ Χ

= Α ,

Α Χ

= Λ ;

2) Α ∩ Χ

= , Α Χ

= Λ ;

3) Α \ (Α \ Χ ) = ;

4) Α \ Χ

= , Α Χ

= Α ;

5) Α \ (Α \ Χ ) = ,

∩

= .

6. Найдите решение системы уравнений

\ Α

если известно, что Β

Α ,

∩ Κ

Теория множеств

7. Каждое из следующих утверждений либо докажите, либо покажите

при помощи диаграмм Эйлера-Венна, что оно не всегда верно:

(

Α Β

)

∩ Κ = Α

( Β ∩ Κ) ;

(

Α \ Β

)

Β = Α ;

(

Α Β

)

\ Β = Α

;

(

Α ∩ Β

)

\ Α =

;

Κ) \( Β Κ) ;

(

Α \ Β

)

Κ = (

(Α ∩

)

(Β ∩

)

;

Β = (Α ∩

)

(Β ∩

) Α = .

8. Верно ли, что:

1) Α Β = Α Κ Β = Κ ;

Α ∩ Β = Α ∩ Κ Β = Κ ;

Α Β = Α Κ и Α ∩ Β = Α ∩ Κ Β = Κ .

9. Докажите:

(

Α Β

)

∩ Κ = Α ( Β ∩ Κ) Α Κ ;

Α = Β Α + Β = ;

Α Β

= Α = Β = ;

(

Α Β

)

\ Β = Α Α ∩ Β = ;

Α \ Β = Α Β \ Α = Β ;

Α Β = Α \ Β Β = ;

Α \ Β = Α ∩ Β Α = ;

Α Β Κ Α Κ и Β Κ ;

Α Β Κ Α \ Β Κ ;

10)

Κ Α ∩ Β Κ Α и Κ Β ;

11)

Α ∩ Β = Α Β Α = Β ;

12)

Α Β Κ Α Β = Β ∩ Κ ;

13)

Α Β Α \ Κ Β \ Κ ;

14)

Β Α

и Κ = Α \ Β Α = Β Κ ;

15)

Α Β = Α Α ∩ Β = Β .

10. Объединением семейства множеств Α i (i Ι)

называется множество

Υ Α i = {x : j Ι x Α j } .

i Ι

Пересечением семейства множеств Α i (i Ι) называется множество

Ι Α i = {x : j Ι x Α j } .

Найдите

[− n, n] .

i Ι

{ x

R : x > α} . Найдите Ι Χ

α , Υ

Χ α .

11. Пусть Χ α

α Ν

12. Приведите пример:

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.04.20156.63 Mб145УМО-матвед-конец.doc
#
02.04.2015713.73 Кб36УП ЭКГ-1 ред.doc
#
02.04.2015739.33 Кб35УП ЭКГ-1 ред.doc
#
02.04.2015721.41 Кб25УП ЭКГ-1 ред.doc
#
02.04.2015372.78 Кб43Учебная практика бакалавров.pdf
#
02.04.2015785.19 Кб95Учебник мануалов ВГУ по дискретке.pdf
#
02.04.201530.72 Кб59Учебники по микроэкономике Электронные адреса.doc
#
02.04.201532.77 Кб18Учебники по микроэкономике Электронные адреса.doc
#
14.03.20161.32 Mб35Учебное пособие программные стат комплексы.doc
#
02.04.2015165.18 Кб12учебный отчет4.docx
#
02.04.20152.97 Mб307учпосООКМлабраб.doc