
Конспект лекций по ТАУ
.pdfПредельным вариантом П-регулятора является регулятор релейного типа, который работает по знаку ошибки:
u(t) = umaxsign(e).
Такой закон управления обеспечивает минимальное время нарастания, но может вызывать большое перерегулирование.
В промышленности массово используются аналоговые и цифровые регуляторы по отклонению, называемые ПИДрегуляторами (сокращение от пропорционально-интегрально- дифференциальный).
Основное уравнение ПИД-регулятора имеет следующий вид:
|
|
1 |
t |
de(t) |
||
u(t) = u0 |
+ k e(t) + |
|
e(τ)dτ + Td |
|
, |
|
Ti |
dt |
|||||
|
|
∫0 |
|
|||
где k – усиление регулятора; Ti и Td – постоянные времени интегрирования и дифференцирования; u0 – поправочное значение (смещение), которое может быть нулевым.
Раскрывая скобку при u0 = 0, можно записать:
t |
de(t) |
|
|
u(t) = kPe(t) + ki ∫ e(τ )dτ + kd |
, |
||
|
|||
0 |
dt |
||
|
|
||
где kp, ki, kd – коэффициенты, выбираемые в процессе проектирования.
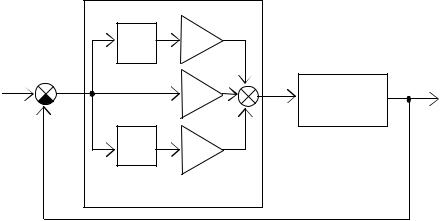
Таким образом, закон управления включает три слагаемых, каждое из которых оказывает свое влияние на переходный про-
цесс (рис. 1.19).
Увеличение коэффициента kp уменьшает время нарастания и установившуюся ошибку. Увеличение коэффициента ki эффективно устраняет установившуюся ошибку. Рост kd увеличивает устойчивость системы, уменьшает перерегулирование и улучшает переходную характеристику.
41
|
d/d |
kd |
|
|
g(t) |
e(t) |
|
u(t) |
y(t) |
|
|
|
Объект |
|
|
|
kp |
|
|
|
|
управления |
|
|
|
|
|
|
|
|
∫ |
ki |
|
|
|
ПИД-регулятор |
|
|
|
|
Рис. 1.19. Структура ПИД– регулятора |
|
||
Влияние каждого коэффициента на переходный процесс в замкнутой системе показано в табл.1.1.
Таблица 1.1 Влияние коэффициентов ПИД-регулятора
|
tн |
δ |
tр |
eуст |
|
|
|
|
|
kp |
Уменьшает |
Увеличивает |
Слабо влияет |
Уменьшает |
|
|
|
|
|
ki |
Уменьшает |
Увеличивает |
Увеличивает |
Исключает |
|
|
|
|
|
kd |
Слабо влияет |
Уменьшает |
Уменьшает |
Слабо влияет |
|
|
|
|
|
На практике часто используются упрощенные версии ПИД- регулятора: П-, И-, ПД- и ПИ-регуляторы, в которых используются не все три, а одно или два слагаемых из формулы ПИДрегулятора. Популярность ПИД-регуляторов вызвана тем, что их использование возможно без процедуры построения математической модели объекта управления. При этом лишь предпола-
42
гается, что объект управления принадлежит к классу объектов, для которого ПИД-регулятор может выступать в качестве приближенной обратной модели (см. рис. 1.9). Экспериментально подбирая значения коэффициентов закона управления, можно получить приемлемое качество переходного процесса.
Например, рассмотрим метод Зиглера– Николса настройки ПИД-регулятора для объекта с самовыравниванием.
Перепишем закон управления ПИД – регулятора в виде:
|
+ Td s + |
1 |
|
|
|
|
|||
|
||||
H (s) = kp 1 |
|
. |
||
|
|
Ti s |
||
Рассмотрим первый вариант (замкнутая система).
3.Коэффициенты kd и ki устанавливаются равными нулю, а коэффициент kp увеличивается до тех пор, пока в системе не возникнут автоколебания.
4.Обозначим предельное значение kp как P, а период автоколебаний как T. Значения коэффициентов П, ПИ или ПИД-регулятора рассчитываются в соответствии с табл. 1.2.
|
|
|
|
Таблица 1.2. |
|
Расчет коэффициентов регулятора |
|
||
|
|
|
|
|
|
|
KP |
Ti |
Td |
|
|
|
|
|
П |
|
0,5P |
|
|
|
|
|
|
|
ПИ |
|
0,45P |
T/1,2 |
|
|
|
|
|
|
ПИД |
|
0,6P |
T/2 |
T/8 |
|
|
|
|
|
Однако такой подход не может обеспечить высокое качество управления, которое может быть достигнуто только при использовании математического описания САУ.
43
Вопросы для самопроверки
−Для решения каких задач разрабатывались в древности первые автоматические устройства?
−Какие автоматические устройства получили распространение в средневековье?
−Какие задачи решали первые регуляторы в промышлен-
ности?
−Что такое системы прямого и непрямого регулирования?
−Кто первым предложил использовать дифференциальное уравнение в качестве модели регулятора?
−Кто первым ввел понятие линеаризации дифференциальных уравнений?
−Кем были заложены основы создания автопилотов?
−Кем была создана теория управления летательными аппаратами?
−Кто заложил математические основы теории устойчиво-
сти?
−Кем было предложено использовать частотные характеристики для анализа и синтеза систем управления?
−Из каких частей состоит система автоматического управления?
−Какая система управления является одномерной (скаляр-
ной)?
−Какая система управления является многомерной (векторной)?
−Что такое динамический объект управления?
−Какая система управления является непрерывной?
−Какие существуют виды непрерывных систем?
−Что такое принцип суперпозиции?
−Какая система называется стационарной?
−Какая система называется физически реализуемой?
−Какая система называется детерминированной?
44
−Какая система называется стохастической?
−Какая система называется дискретной?
−Что такое следящая система?
−Что такое система стабилизации?
−Что такое система программного регулирования?
−Что такое адаптивная система управления?
−Что такое статическая и астатическая система?
−Как описывается структурная схема системы автоматического управления?
−Что такое разомкнутая система управления?
−Что такое замкнутая система управления?
−В чем заключается задача анализа САУ?
−В чем заключается задача синтеза САУ?
−Какие этапы включает в себя процесс проектирования
САУ?
−Что такое метод разделения движений при синтезе САУ?
−Какие два подхода могут быть использованы при разработке модели объекта управления?
−Что такое модель типа «черный ящик»?
−С какой целью используется линеаризация?
−Какой вид имеет статическая характеристика линейной системы?
−Что такое рабочая точка?
−Как выполняется линеаризация дифференциального уравнения?
−В чем смысл задачи идентификации модели?
−Какой входной сигнал используется для получения переходной функции?
−Какие условия должны выполняться при получении кривой разгона объекта управления?
−Что такое частотные характеристики объекта управле-
ния?
45
−Какие характеристики используются для описания переходного процесса?
−Что такое время нарастания?
−Что такое время переходного процесса?
−Что такое перерегулирование?
−Какое свойство объекта управления называется самовыравниванием?
−Какая формула описывает закон пропорционального управления?
−Какой формулой описывается работа релейного регуля-
тора?
−Что представляет собой ПИД-регулятор?
−Какое влияние оказывает на переходную характеристику пропорциональная компонента ПИД-регулятора?
−Какое влияние оказывает на переходную характеристику дифференциальная компонента ПИД-регулятора?
−Какое влияние оказывает на переходную характеристику интегральная компонента ПИД-регулятора?
−В чем заключается методика экспериментальной настройки ПИД-регулятора?
46
2.ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
2.1.Преобразование Лапласа
Рассмотрим систему автоматического управления, описываемую линейным дифференциальным уравнением вида
a |
|
d n y(t) |
|
+ a |
n −1 |
d n −1 y(t) |
+ ... + a |
dy(t) |
+ a y(t) = |
||||||
|
|
dt n |
|
|
|
||||||||||
|
n |
|
|
dt n −1 |
1 |
dt |
0 |
||||||||
= b |
|
d mu(t) |
+ b |
|
d m −1u(t) |
+ ... + b u(t), |
|
||||||||
|
|
|
|
||||||||||||
|
|
m |
|
dt m |
|
|
m −1 dt m −1 |
|
0 |
|
|
||||
где u(t) – входной процесс; y(t) – выходной процесс; ai, bi, – постоянные коэффициенты; n, m – постоянные числа.
В реальных системах всегда выполняется условие физической реализуемости системы n >= m.
Если ввести обозначение p для оператора дифференцирования p = d/dt, то можно записать уравнение в операторной форме:
(an p n + an −1 p n −1 + ... + a1 p + a0 ) y(t) = = (bm p m + bm −1 p m −1 + ...b1 p + b0 )u(t).
Вводя обозначения для полиномов, получаем
A( p) y(t) = B( p)u(t).
Рассмотрим отношение выходного сигнала системы к ее входному сигналу:
47

y(t) = B( p) =
W ( p) .
u(t) A( p)
Это выражение дает нестрогое определение W(p) – передаточной функции системы. Строгое определение может быть дано с использованием преобразования Лапласа, которое заменяет дифференциальное уравнение алгебраическим.
Преобразованием Лапласа называют интегральное преобразование
∞
X (s) = ∫ x(t)e−st dt ,
0
определяющее соответствие между функцией x(t) вещественного переменного и функцией X(s) комплексного переменного s.
При этом x(t) называют оригиналом, а X(s) – изображением по
Лапласу.
Предполагается, что оригинал обладает следующими свойствами:
3.функция x(t) определена (не имеет точек разрыва) и дифференцируема на всей положительной числовой полуоси;
4.функция x(t) = 0 при t < 0;
5.существуют такие числа М и α, что
x(t) ≤ Meαt , 0 ≤ t ≤ ∞.
Практически во всех случаях эти условия выполняются. Символическая запись преобразования Лапласа:
X(s) = L{x(t)},
где L{ }– оператор преобразования Лапласа. Рассмотрим пример.
∞ |
∞ |
1 |
|
|
L{e−at } = ∫ e−at e−st dt = ∫ e−( s+a )t dt = |
. |
|||
|
||||
|
||||
0 |
0 |
s + a |
||
|
|
|||
48
На практике обычно нет необходимости вычислять преобразование Лапласа для заданного оригинала, поскольку для большинства важнейших функций времени изображения по Лапласу известны (см. табл. 2.1).
Преобразования Лапласа |
|
|
|
|
|
|
|
|
Таблица 2.1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наименование |
|
|
Оригинал |
Изображение |
|
||||||||||||||
|
|
Лапласа |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||
Единичная им- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пульсная функ- |
|
|
|
δ(t) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
ция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Единичная сту- |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
пенчатая |
|
|
1(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
s |
|
|||||||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Степенная |
|
|
t n ×1(t) |
|
|
|
|
|
|
n! |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
s n+1 |
||||||||||
Экспонента |
|
|
e−αt ×1(t) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
s |
+ α |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Экспонента |
|
|
t n e |
−αt ×1(t) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n +1 |
|||||||||||
|
|
|
|
|
|
(s + α) |
|
||||||||||||
Смещенная экс- |
|
1 |
(1 - e−αt ) ×1(t) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
понента |
|
|
|
|
s(s + α) |
|
|||||||||||||
|
a |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Синусоида |
|
|
sinβt ×1(t) |
|
|
|
s2 |
|
β |
|
|||||||||
|
|
|
|
|
|
+ β2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49

Косинусоида |
|
cosβt ×1(t) |
|
|
p |
|
|||
|
|
|
|
|
|
|
|||
|
|
s2 + β2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
Затухающая си- |
e−αt sin βt ×1(t) |
|
|
β |
|
||||
нусоида |
|
(s + α )2 + β2 |
|
||||||
|
|
|
|
|
|
|
|
||
Затухающая ко- |
e |
−αt |
cosβt ×1(t) |
|
|
s + α |
|
||
синусоида |
|
|
(s + α)2 + β2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
Обратное преобразование Лапласа описывается формулой
σ+ j∞
x(t) = 1 ∫ X (s)est ds.
2πj σ− j∞
В символических обозначениях:
x(t) = L-1{X(s)}.
Рассмотрим ряд свойств преобразования Лапласа, которые потребуются в дальнейшем изложении.
1) Линейность преобразования:
L{αy1(t) + βy2(t)} = αL{y1(t)} + βL{y2(t)} = αY1(s) + βY2(s). 2) Дифференцирование оригинала:
L{dY(t)/dt} = sY(s) – y(0),
где y(0) – начальное условие.
В табл. 2.2 показаны правила преобразования по Лапласу для
производных различных порядков. |
|
|
Дифференцирование оригинала |
Таблица 2.2 |
|
|
|
|
Оригинал |
Изображение |
|
y(t) |
|
Y(s) |
|
|
|
50
