
Конспект лекций по ТАУ
.pdf
4.Частотные методы анализа и синтеза
4.1.Преобразование Фурье
Частотные характеристики позволяют косвенно судить о процессах, происходящих в системах автоматического управления (не решая дифференциальных уравнений, описывающих данную систему). Они могут быть получены экспериментальным путем.
Рассмотрим линейную стационарную систему, описываемую дифференциальным уравнением:
(an p n + an−1 p n−1 + ... + a1 p + a0 ) y(t) = = (bm p m + bm−1 p m−1 + ... + b1 p + b0 )x(t).
Применим к этому уравнению преобразование Фурье
∞ |
∞ |
X ( jω) = ∫ x(t)e− jωt dt , |
Y ( jω) = ∫ y(t)e− jωt dt . |
−∞ |
−∞ |
Частотная ПФ определяется как отношение преобразований Фурье выходного и входного сигнала:
W ( jω) = B( jω) = bn ( jω)m + ... + b1 ( jω)+ b0 .
A( jω) an ( jω)n + ... + a1 ( jω)+ a0
Функция W(jω) характеризует динамические свойства системы и не зависит от характера приложенных к системе воздействий.
Частотная ПФ получается из обычной ПФ W(s) при чисто мнимых значениях s, то есть при s = jω. Зная частотную ПФ линейной стационарной системы, можно найти реакцию системы на гармонический входной сигнал в установившемся режиме.
151

Пусть входной сигнал системы имеет амплитуду a и частоту ω, т.е. описывается формулой:
x = a sin(ωt) .
Выходной сигнал будет иметь амплитуду А1 и отличаться от входного по фазе на величину φ (фазовый сдвиг):
y = A1 sin(ωt + ϕ) .
Таким образом, можно рассчитать усиление по амплитуде:
A = A1 . a
Для каждой частоты входного сигнала ω будут свои A и φ.
Если на вход подавать сигнал с постоянной амплитудой и изменяющейся частотой, то изменение амплитуды и сдвига фазы выходного сигнала будут определяться динамическими свойствами звена. Если для различных частот, начиная с нулевой, измерить усиление по амплитуде и фазовый сдвиг, то получаются частотные характеристики звена: A(ω) – амплитудно-частотная
характеристика (АЧХ) и ϕ(ω) – фазочастотная характери-
стика (ФЧХ).
Для суждения о реакции звена на синусоидальный сигнал достаточно исследовать его реакцию на гармонический сигнал вида:
X ( jω) = e jωt .
Тогда выходной сигнал
152

Y ( jω) = A(ω)e j (ωt +ϕ (ω)) .
Частотная ПФ
W ( jω) = Y ( jω) = A(ω)e jϕ (ω) .
X ( jω)
Эта формула является представлением частотной ПФ в полярных координатах.
Можно также записать частотную ПФ в алгебраической форме:
W ( jω) = U (ω) + jV (ω).
Поскольку W(jω) является комплексным выражением, ее можно представить в виде
W ( jω) = a1 (ω) + jb1 (ω) . a2 (ω) + jb2 (ω)
Для нахождения вещественной и мнимой частей частотной ПФ необходимо домножить числитель и знаменатель на сопряженную знаменателю величину, а затем провести разделение:
W ( jω) = |
|
a1 (ω) + jb1 (ω) |
= |
(a1 (ω) + jb1 |
(ω))(a2 (ω) − jb2 (ω)) |
= |
|||||||||
a |
(ω) + jb (ω) |
(a (ω) + jb (ω))(a |
(ω) − jb (ω)) |
||||||||||||
|
|
|
2 |
2 |
|
|
1 |
|
2 |
2 |
|
2 |
|
|
|
= |
a1 (ω)a2 (ω) + b1 (ω)b2 (ω) |
+ j |
a2 (ω)b1 |
(ω) − a1 (ω)b2 |
(ω) |
= |
|
||||||||
a2 |
(ω) + b2 (ω) |
|
|
a2 |
(ω) + b2 |
(ω) |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
||
= U (ω) + jV (ω).
Таким образом:
153

U (ω) + jV (ω) = A(ω)e jϕ (ω) ,
где
|
|
|
|
|
|
|
|
|
|
|
a2 |
+ b2 |
|
|
|
|
||
A(ω) = |
|
= U 2 (ω) + V 2 |
(ω) = |
|
|
|
||||||||||||
W ( jω) |
|
|
|
1 |
1 |
|
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
+ b2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
V (ω) |
|
|
b |
|
|
|
b |
|
|
||||||
ϕ(ω) = arg(W ( jω)) = arctg |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= arctg |
|
|
|
|
− arctg |
|
.. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U (ω) |
|
|
a1 |
|
|
|
a2 |
|
|||||||
U (ω) = A(ω) cosϕ(ω),
V (ω) = A(ω) sinϕ(ω).
Графики функций U(ω) и V(ω) называют соответст-
венно вещественной и мнимой частотной ха-
рактеристиками.
Пример 4.1. Рассмотрим АЧХ и ФЧХ апериодического звена 1-го порядка.
Частотная характеристика апериодического звена имеет вид:
|
k (1 − jωT ) |
k |
|
jkωT |
|
|
W ( jω) = |
(1+ jωT )(1− jωT ) |
= |
|
− |
|
= |
1+ ω2T 2 |
1+ ω2T 2 |
|||||
= U (ω) + jV (ω). |
|
|
|
|
||
АЧХ и ФЧХ выражаются из алгебраического представления частотной характеристики:
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
||||
A(ω) = |
= U 2 (ω) + V 2 (ω) = |
|
|
|||||||
|
|
|
|
|
, |
|||||
jωT + 1 |
|
|
|
|||||||
|
|
|
1 |
+ ω2T 2 |
||||||
|
|
k |
|
= arctg(0) − arctg(ωT )= − arctg(ωT ). |
||||||
ϕ (ω) = arg |
|
|
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
jωT + 1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
По этим формулам можно построить графики (рис. 4.1). График ФЧХ показывает, что с ростом частоты коэффициент
154
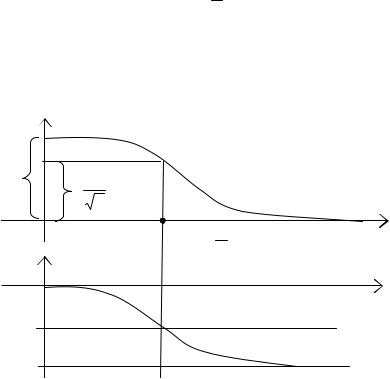
усиления падает тем быстрее, чем больше постоянная времени звена T. При нулевой частоте усиление максимально и равно k. Сигналы низких частот апериодическое звено хорошо пропускает, а сигналы высоких частот ослабляются.
Полосой пропускания звена называется диапазон частот
0 ≤ ω ≤ T .
Частота
ωс = 1 .
T
называется частотой среза.
Длительность переходного процесса в апериодическом звене ≈ 3Т, поэтому чем шире полоса пропускания (т.е. чем меньше Т), тем быстрее протекают переходные процессы в системе.
|
A |
|
|
k |
k |
|
|
|
2 |
|
|
|
ωс |
= 1 |
ω |
|
φ |
T |
|
|
|
|
|
|
|
|
ω |
–π/4
–π/2
Рис. 4.1. АЧХ и ФЧХ апериодического звена 1-го порядка
Из графиков АЧХ и ФЧХ можно получить один график –
155
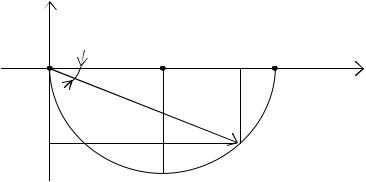
АФЧХ, который для апериодического звена будет иметь вид, показанный на рис. 4.2.
Im(W(jω))
ω= ∞ |
ω |
|
= |
1 |
|
|
с |
T |
U(ω) ω= 0 |
||||
|
|
|||||
|
|
|
ω |
Re(W(jω)) |
|
|
A(ω) |
|
V(ω) |
|
Рис. 4.2. АФЧХ апериодического звена 1-го порядка
4.2. Логарифмические частотные характеристики
В практических расчетах удобно применять графики частотных характеристик, построенные в логарифмическом масштабе. Это обеспечивает ряд преимуществ:
1.упрощается процесс построения характеристик, поскольку график аппроксимируется отрезками прямых;
2.оказывается удобным рассматривать достаточно большой диапазон частот;
3.вместо умножения характеристик последовательно соединенных звеньев надо складывать их логарифмы.
Логарифмические частотные характеристики часто называют
диаграммами Боде.
Обычно используют амплитудную характеристику в виде за-
висимости 20lgA(lgω), называемой логарифмической амплитуд- но-частотной характеристикой (ЛАЧХ). Фазовую характери-
стику в виде зависимости ϕ(lgω) называют логарифмической фазочастотной характеристикой (ЛФЧХ).
156

На графиках ЛАЧХ и ЛФЧХ ось абсцисс разбивается на одинаковые участки – декады. В пределах каждой декады частота увеличивается в 10 раз (рис. 4.3).
декада
0.1 |
1 |
10 |
100 |
ω |
Рис. 4.3. Разбиение оси частот на декады
Вместо lgω обычно записывается значение самой частоты, так что масштаб на оси абсцисс получается неравномерный. В начало координат можно помещать любое значение частоты, в зависимости от того, какое исследование нужно выполнить.
На графике ЛАЧХ по оси ординат откладывается величина
L(ω) = 20lgA,
которая измеряется в децибелах (1децибел = 0,1 бела).
Один бел соответствует усилению сигнала по мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т.д.
Так как обычно измеряют не мощность сигнала, а его амплитуду, а мощность сигнала пропорциональна квадрату амплитуды, то усилению сигнала по мощности в 10 раз будет соответствовать lgA2 =1 или 2lgA = 1. Соответственно, усиление сигнала в децибелах, выраженное через отношение амплитуд равно 20lgА.
Таким образом, каждые 20 децибелл (дБ) на графике ЛАЧХ соответствуют усилению амплитуды в 10 раз (рис. 4.4).
L(ω, дб) |
А = |
|
|
40 |
|
30 
А = 10 |
157 |
20 
10 
Рис. 4.4. Усиление амплитуды в децибеллах
Можно показать, насколько увеличивается A(ω) при изменении L(ω) на один децибел:
L(ω) = 20lgA = 1 = lg10 → A20 = 10 → A ≈ 1,12.
Отрицательные значения L(ω) соответствуют ослаблению амплитуды (A < 1).
Нулевое значение L(ω) соответствует единичному значению усиления амплитуды:
L(ω) = 20lgA = 0 = lg(1) → A = 1.
При построении ЛФЧХ используют логарифмический масштаб по оси абсцисс и натуральный по оси ординат. Использовать логарифмический масштаб по оси ординат не имеет смысла, поскольку фазовый сдвиг при последовательном соединении звеньев и так складывается.
Пример 4.2. Рассмотрим ЛАЧХ и ЛФЧХ апериодического звена 1-го порядка. Ранее были получены формулы:
158
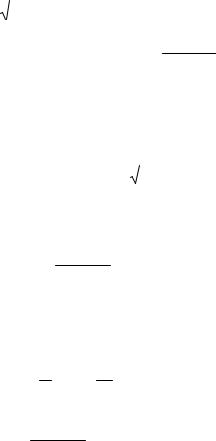
A(ω) = |
|
|
k |
ϕ(ω) = − arctg(ωT ). |
|
|
|
|
, |
||
|
|
|
|||
1 |
+ ω2T 2 |
|
|||
Тогда
L(ω) = 20 lg A(ω) = 20 lg k − 20 lg 
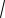 1 + ω2T 2 .
1 + ω2T 2 .
Рассмотрим асимптоты – прямые, к которым стремится ЛАЧХ при малых значениях частоты (ω << 1/T) и при больших значениях частоты (ω >>1/T), т.е. при ω → 0 и при ω → ∞.
При ω → 0 имеем
|
|
|
L(ω) ≈ 20 lg k , так как |
1 + ω2T 2 ≈ 1. |
|
Эта асимптота представляет собой прямую, параллельную оси абсцисс на уровне 20lg(k).
При ω → ∞ имеем
− 20 lg 
 1 + ω2T 2 → −∞.
1 + ω2T 2 → −∞.
Эта асимптота представляет собой наклонную прямую.
Для вычисления наклона прямой рассмотрим изменение усиления в границах одной декады:
1≤ ω ≤ 10 .
ТТ
Поскольку при больших частотах
20 lg 
 1 + ω2T 2 ≈ 20 lg(ωT ),
1 + ω2T 2 ≈ 20 lg(ωT ),
Можно записать
|
10 |
|
|
1 |
|
|
|
|
|
|
|
|||
L(ω) = L |
|
|
− L |
|
|
= |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
T |
|
|
T |
|
|
|
|
|
|
|
|||
|
|
|
|
10 |
|
|
|
|
|
1 |
|
|
||
= 20 lg k − |
20 lg |
|
|
|
T |
|
|
− |
20 lg k − 20 lg |
|
T |
= −20. |
||
|
|
|
|
|||||||||||
|
|
|
T |
|
|
|
T |
|
|
|||||
|
|
|
|
|
|
|
||||||||
159
Наклон прямой оказывается равным –20 дБ/дек (рис. 4.5).
L(ω)
20lgk |
|
декада |
|
|
|
ω = 1 |
ωс |
ω |
T |
|
|
|
20 дБ |
|
Рис. 4.5. ЛАЧХ апериодического звена 1-го порядка
Наибольшее отклонение ЛАЧХ от АЧХ будет в точке ω = 1/T, которое равно:
=20 lg k − (20 lg k − 20 lg 
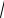 T 2ω2 +1)=
T 2ω2 +1)=
=10 lg(T 2ω2 +1) = 10 lg 2 ≈ 3,03 дБ.
Частота, при которой ЛАЧХ пересекает ось 0 дБ, называется
частотой среза системы ωс.
Пример 4.3. Рассмотрим ЛАЧХ и ЛФЧХ колебательного звена.
W (s) = |
|
|
k |
, |
T1 < 2T2 . |
|
T 2 s2 |
+ T s + 1 |
|||||
2 |
1 |
|
|
|
||
W ( jω) = |
|
|
k |
|
. |
|
|
− T 2ω2 |
+ jωT + 1 |
||||
|
|
2 |
|
1 |
|
|
160
