Файловый архив студентов. Файловый архив студентов.
1308 вузов, 5223 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский государственный университет аэрокосмического приборостроения
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Конспект лекций по ТАУ

.pdf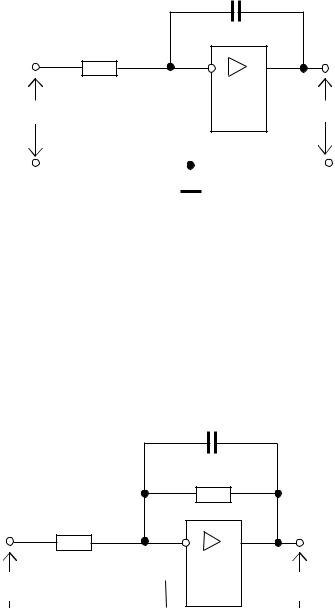
Скачиваний:
595
Добавлен:
02.04.2015
Размер:
1.24 Mб
Скачать
☆

Используя эту формулу, можно получать ПФ для конкретных схем на базе ОУ.

Рассмотрим схему интегратора на ОУ, показанную на рис. 4.36.

C

R

U1

 

U2

 

 

 

 

 

 

 

 

 

 

Рис. 4.36. Схема интегратора на базе ОУ

W (s) = −

Zос (s)

= −

1

= −

k

,

 

 

 

 

Z1 (s)

RCs

 

s

где k = 1/RC.

Еще один пример схемы показан на рис. 4.37.

C

R2

R1

211

U1

 

U2

Рис. 4.37. Пример активного корректирующего звена

Для этой схемы

 

 

 

 

 

 

 

 

1

 

R

 

 

 

 

 

 

 

 

 

 

Zoc

(s) =

 

 

Cs

=

R2 .

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

+ R2

 

 

1+ R2Cs

 

 

 

 

 

 

 

 

 

 

 

Cs

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким образом:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W (s) =

U 2 (s)

= −

Zос (s)

= −

 

 

R2

= −

k

 

,

 

 

 

R (1+ R Cs)

Ts +1

 

U

(s)

 

Z (s)

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

1

2

 

 

 

 

 

где k = -R2/R1 – коэффициент усиления; T = R2С – постоянная времени.

Заметим, что ОУ является линейной системой, поэтому к нему применим принцип суперпозиции (здесь не будем учитывать существующие для реальной микросхемы ограничения параметров).

212

Например, если ОУ имеет три входа (рис. 4.38), то выходной сигнал будет складываться из трех составляющих и для каждого из трех входов будет своя ПФ.

 

Rос

R

 

U1

 

R2

 

U2

Uвых

R

U3

 

Рис. 4.38. Суммирующий ОУ

W (s) =

Uвых (s)

= −

Roc

;

W (s) =

Uвых (s)

= −

Roc

;

 

 

 

 

 

 

1

U1

(s)

 

R1

 

2

 

 

U2

(s)

 

R2

 

 

 

 

 

 

 

 

 

W (s) =

Uвых (s)

= −

Roc

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

U3

(s)

 

 

R3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Uвых (s) = −(W1 (s)U1 (s) +W2 (s)U2 (s) +W3 (s).U3 (s)).

Для определения параметров конкретного корректирующего звена удобно переходить от ПФ к дифференциальным уравнениям.

213

Например, рассмотрим реализацию колебательного звена:

W (s) =

 

K

< 2T2 .

 

 

; T1

T 2 s 2

 

 

+ T s + 1

 

2

1

 

 

Представим ПФ в виде

W (s) =

Y (s)

=

 

 

 

K

;

 

 

 

 

+ 2ξTs +1

 

 

X (s) T 2 s2

.

T = T2

, ξ =

 

T1

 

 

 

 

 

2T2

 

 

 

 

 

 

 

 

Перейдем далее от ПФ к дифференциальному уравнению в операторной форме

y(T 2 s2 + 2ξTs + 1) = Kx

и разрешим его относительно старшей производной:

 

s2 y =

K

 

x -

2ξ

sy -

1

 

y .

 

T 2

 

 

 

T 2

 

 

 

 

 

 

 

 

T

 

 

 

 

 

Введем обозначения:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k =

K

;

k

 

=

1

 

;

k

 

=

2ξ

.

 

 

T 2

 

 

1

 

T 2

 

 

2

 

 

 

 

 

3

 

 

T

Пример 4.9. Допустим, что заданы конкретные параметры звена:

W (s) =

1

 

;

0,1s2 + 0,02s +1

 

T = T2 = 0,3162;

ξ =

 

0,02

 

= 0,0316.

 

 

 

 

× 0,3162

 

2

 

214

Следовательно

k1 = k2 = 1/T2 = 10;

k3 = 2ξ/T = (2·0,0316)/0,3162 = 0,1999.

Тогда получается следующая схема, включающая три ОУ (рис. 4.39).

C1

R4

C2

 

 

R3

R4

R5

R2

 

 

R1

DA2

Uвых

DA1

DA3

Uвх

 

 

Рис. 4.39. Реализация колебательного звена на базе ОУ

В этой схеме DA2 и DA3 играют вспомогательную роль, их коэффициенты передачи равны 1, так что

215

можно выбрать, например, R4 = R5 = 1мОм, а С2 = 1мкФ.

Параметры С2, R1, R2 и R3 должны обеспечивать рассчитанные значения k1, k2 и k3. Например, при выборе С2 = 1мкФ, получаем:

k1 = k2

=

 

1

 

 

 

=

 

1

 

 

 

= 10

R1 = R2 = 100кОм,

R

(1×10−6 )

 

R (1×10−6 )

 

 

 

 

 

 

 

 

1

 

 

 

 

 

2

 

 

 

 

 

 

 

k3

= k2

=

 

 

 

1

 

= 0,2

R3 = 5мОм .

 

 

 

 

 

 

 

 

R

(1×10−6 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

Пример 4.12. Рассмотрим аналоговую реализацию ПИД-регулятора, уравнение которого имеет следующий вид:

 

1

t

de(t)

u(t) = K ke(t) +

 

e(τ)dτ + Td

 

,

Ti

dt

 

∫0

 

где e(t) – ошибка регулирования; k – коэффициент регулятора; К – масштабный множитель; Ti и Td – постоянные времени интегрирования и дифференцирования.

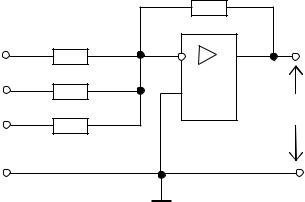
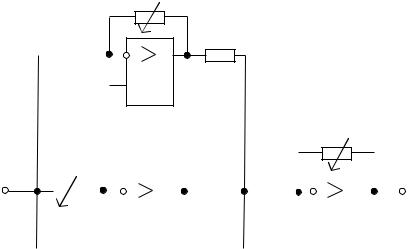
Схема ПИД-регулятора изображена на рис. 4.40.

k

Z1(s)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

K

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ti

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

216 e(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 4.40. Аналоговый ПИД-регулятор

Регулятор имеет три настроечных сопротивления, с помощью которых подобрать параметры закона управления, используя, например, методику Зиглера– Николса.

Аналоговые ПИД-регуляторы, как и вообще аналоговые корректирующие звенья, имеют ряд недостатков,

втом числе:

1.разброс параметров полупроводниковых приборов даже для элементов одного и того же типа;

2.зависимость параметров от окружающей среды и времени;

3.сложность и пониженная точность реализации нелинейных операций;

4.снижение надёжности при возрастании сложно-

сти;

217

5. жесткость структуры, т.е. необходимость замены устройства при изменении требований к САУ.

Эти недостатки препятствуют использованию аналоговых корректирующих устройств в высокоточных системах стабилизации, в прецизионных электроприводах и других сложных системах.

218

Вопросы для самопроверки

−Каким путем можно получить частотные характеристики системы?

−Что такое частотная передаточная функция?

−Как получить частотную ПФ из обычной ПФ

−Как параметры выходного сигнала системы меняются при подаче на вход гармонического сигнала?

−Что описывает АЧХ системы?

−Что описывает ФЧХ системы?

−Как построить АЧХ системы по ее ПФ?

−Как построить ФЧХ системы по ее ПФ?

−Как описать частотную ПФ в полярных координатах?

−Как описать частотную ПФ в алгебраической форме?

−Какой вид имеет АЧХ и ФЧХ апериодического звена 1-го порядка?

−Как ведет себя коэффициент усиления апериодического звена с ростом частоты?

−Как связаны полоса пропускания апериодического звена и длительность переходного процесса?

−Какие преимущества дает использование ЛЧХ?

−Как описывается ось частот при использовании ЛЧХ?

−Как меняется частота в пределах декады?

−Какая величина откладывается на графике ЛАЧХ по оси ординат?

219

−Какому значению усиления сигнала по мощности соответствует один бел?

−Во сколько раз меняется амплитуда при увеличении ЛАЧХ на один децибел?

−Какое значение оси ординат ЛАЧХ соответствует единичному значению усиления амплитуды?

−Какая область значений оси ординат ЛАЧХ соответствует ослаблению амплитуды?

−Где находится частота среза на графике ЛАЧХ?

−Какой вид имеют ЛАЧХ и ЛФЧХ апериодического звена 1-го порядка?

−Какой вид имеют ЛАЧХ и ЛФЧХ колебательного звена?

−Почему инерционные звенья называют фильтрами низкой частоты?

−Какой вид имеют ЛАЧХ и ЛФЧХ идеального дифференцирующего и идеального интегрирующего звеньев?

−Какой вид имеют ЛАЧХ и ЛФЧХ форсирующего звена?

−Как описывается ЛАЧХ разомкнутой системы при последовательном соединении звеньев?

−Какие шаги включает в себя алгоритм построения ЛАЧХ разомкнутой системы?

−Как строится кривая Михайлова?

−Как формулируется критерий устойчивости Михайлова для линейной системы n-го порядка?

220

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности