§14. Функция распределения

Если F(x) = P(X < x), то функция F(x) называется функцией распределения (интегральной функцией распределения) случайной величины Х, т.е. функция распределения в точке “х”  это вероятность того, что случайная величина Х примет значение, меньшее заданного числа х.

Из определения сразу следуют несколько свойств F(x):

F( = 0, F(+ ) = 1;

F(x)  неубывающая функция (т.е. если x₁ < x₂ , то F(x₁)  F(x₂) ).

Функция распределения для случайной величины дискретного типа имеет “ступенчатый” график. Для случайной величины Х₁ из §13 F(x) запишется так:

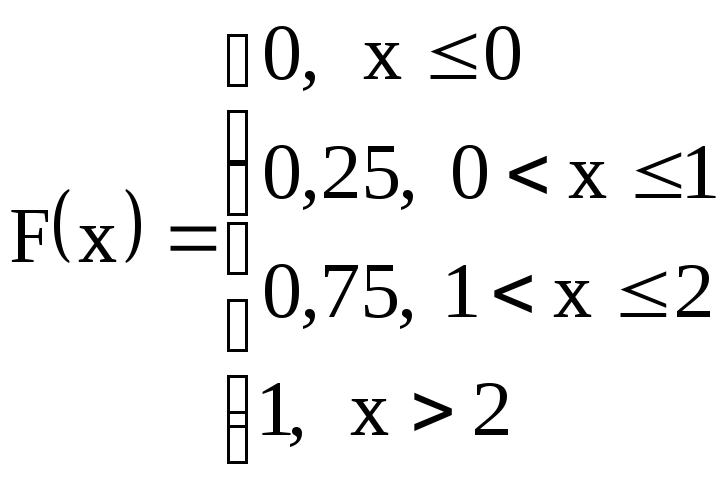
Y

Обратите внимание, что левые концы «ступенек»  выколотые, а правые  нет. Например, F(1) = P(X₁ < 1) = P(X₁ =0) = 0,25;

F(1,1) = P(X₁<1,1) = P(X₁ = 0) + P(X₁ = 1) = 0,75. «Высоты» «ступенек» равны очередным вероятностям, взятым из таблицы : сначала 0,25, затем еще +0,5, и наконец еще +0,25.

Аналогичный график и для другого примера – про домино – только там будет не 2, а 12 «ступенек».

Справедлива формула: P(a X < b) = F(b)  F(a).

§15. Математическое ожидание случайной величины дискретного типа

Математическое ожидание - важнейшая “характеристика положения” случайной величины. Для дискретной величины она вычисляется по формуле

М(Х) = x_{1 ·} p₁ + x_{2 ·} p₂ + ... + x_{k ·} p_k (+...) = ,

где x₁, x₂, ... , x_k, ...  возможные значения случайной величины (верхняя строка таблицы), p₁, p₂, ..., p_k, ...  их вероятности (нижняя строка).

Математическое ожидание  это число, которое выражает среднее значение случайной величины (иначе, среднее значение по распределению). Для примера из §13

М(Х₁) = 0 · 0,25 + 1 · 0,5 + 2 · 0,25 = 1 .

Здесь Х₁  число “орлов”, выпавших при 2 бросках симметричной монеты. М(Х₁)  среднее число “орлов”, выпадающих при 2 бросках симметричной монеты, это число равно 1.

Для другого примера из §13 М(Х₂) = 6.

Отметим два простейших свойства математического ожидания:

1. М (С) = С

2. М (С · Х) = С · М(Х) ( С  постоянная ).

В дальнейшем нам придется вычислять математическое ожидание случайной величины Х². Если случайная величина Х задается таблицей

X	x1	x2	...	xk
P	p1	p2	...	pk

то случайная величина Х² получится после возведения в квадрат возможных значений случайной величины Х, при этом Р(Х = х_к)= = Р(Х² = х_к²) = p_k :

X2	x12	x22	...	xk2
P	p1	p2	...	pk

Поэтому М(Х²) = x₁² · p₁ + x₂² · p₂ + ... + x_k² · p_k = .

В частности, для примера из §13

X2	02	12	22
P	0,25	0,5	0,25

и М(Х²) = 0^{2 ·} 0,25 + 1² · 0,5 + 2² · 0,25 = 1,5

§16. Дисперсия случайной величины

Дисперсия  важнейшая «характеристика рассеивания» случайной величины. Рассеивание оценивается относительно среднего значения случайной величины Х  математического ожидания М(Х). Из всех возможных значений случайной величины Х вычитают число М(Х). Новая случайная величина Y = XM(X) называется отклонением случайной величины Х, причем ее среднее значение М(Y) = 0. Далее рассматривается случайная величина Y². Ее возможные значения неотрицательны. Среднее значение квадрата отклонения М(Y²) также неотрицательно. Оно и называется дисперсией. Итак,

D(X) = M(Y²)=M((X  M(X) )²).

Для вычисления дисперсии используют формулу

D(X) = M(X²)  (M(X))².

Для дисперсии справедливы свойства:

D(C) = 0, D(C · X) = C² · D(X).

Вновь вспомним пример из §13 . Для него М(Х₁) и М(Х₁²) уже подсчитаны выше: М(Х₁) = 1, М(Х₁²) = 1,5. Поэтому D(X) = 1,51² = 0,5 .

Для второго примера из §13 М(Х₂) = 6, М(Х₂²) = 45, D(X) = 45 6² = 9.