Тема № 7. Статистические методы анализа связи

Задание.

1. Из таблицы №1 «Макроэкономические показатели европейских стран» выберите две графы (признаки) данных, соответствующих вашему варианту (см. таблицу №2).

2. Построить аналитическую группировку.

3. Построить парное линейное уравнение связи между признаками.

4. Оценить тесноту связи с помощью эмпирического корреляционного отношения и коэффициента корреляции.

5. Проверить на значимость найденные параметры и регрессионную модель.

6. По полученному уравнению рассчитать прогноз значения У при условии, что величина Х будет на 20% выше своего максимального выборочного значения. (Вероятность 0,95).

Таблица 4

Страна
	ВВП на душу населения, евро (Y)	Занятость, тыс. чел. (X)
Бельгия	436	30
Болгария	446	3
Чехия	1102	7
Дания	1888	27
Германия	7128	37
Эстония	156	7
Ирландия	341	45
Греция	1086	27
Испания	4738	24
Франция	11896	30
Италия	4287	28
Кипр	946	31
Латвия	248	13
Литва	585	5
Люксембург	386	53
Венгрия	1815	6
Нидерланды	266	30
Австрия	835	30
Польша	4438	6
Португалия	226	17
Румыния	1629	3
Словения	383	18
Словакия	468	6
Финляндия	714	29
Швеция	883	30
Великобрит.	2791	35
Хорватия	385	2
Македония	106	1
Турция	1634	14
Исландия	938	5
Норвегия	312	10
Швейцария	1468	12

Решение:

Разобьем совокупность исходных данных на 4 интервала относительно признака-фактора (занятости) таким образом, чтобы количество стран, попавших в каждую группу, было приблизительно одинаково. Результаты аналогичной группировки данных представим в следующей таблице.

Величину интервала определяют по следующей формуле:

h =

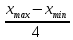
h = 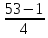= 13

Таблица 5

Аналитическая группировка

Занятость, тыс. чел.	Количество стран в отдельной группе	ВВП на душу населения, евро
1	2	3
1-6	9	10810
6-18	6	5529
18-29	7	12713
29-53	10	25908
Итого:	32	-

Следовательно, с ростом занятости населения ВВП на душу населения увеличивается. При этом исключение составляет только страны попадающие в интервал [6; 18] (скорее всего, это средние и неблагополучные страны).

Проведем расчет уравнения регрессии (табл. 6)

Таблица 6

Страна
	y		x	X2	Y2		x*y
Бельгия	436		30	900	190096		13080
Болгария	446		3	9	198916		1338
Чехия	1102		7	49	1214404		7714
Дания	1888		27	729	3564544		50976
Германия	7128		37	1369	50808384		263736
Эстония	156		7	49	24336		1092
Ирландия	341		45	2025	116281		15345
Греция	1086		27	729	1179396		29322
Испания	4738		24	576	22448644		113712
Франция	11896		30	900	141514816		356880
Италия	4287		28	784	18378369		120036
Кипр	946		31	961	894916		29326
Латвия	248		13	169	61504		3224
Литва	585		5	25	342225		2925
Люксембург	386		53	2809	148996		20458
Венгрия	1815		6	36	3194225		10890
Нидерланды	266		30	900	70756		7980
Австрия	835		30	900	697225		25050
Польша	4438		6	36	19695844		26628
Португалия	226		17	289	51076		3842
Румыния	1629		3	9	2653641		4887
Словения	383		18	324	146689		6894
Словакия	468		6	36	219024		2808
Финляндия	714		29	841	509796		20706
Швеция	883		30	900	779689		26490
Великобрит.	2791		35	1225	7789681		97685
Хорватия	385		2	4	148225		770
Македония	106		1	1	11236		106
Турция	1634		14	196	2669956		22876
Исландия	938		5	25	879844		4690
Норвегия	312		10	100	97344		3120
Швейцария	1468		12	144	2155024		17616
Сумма:	54960	621		18049	282955102	1312202

Выборочные средние:

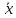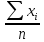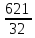= == 19,41

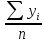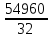= == 1717,5

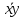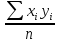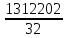= == 41006,31

Выборочные дисперсии:

D(x) = 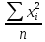-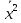=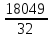-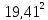= 187,43

D(y) = 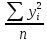-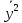=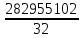-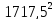= 5892540,69

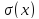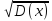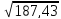= == 13,69

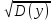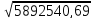= == 2427,46

Ковариация:

cov (x,y) =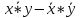= 41006,31 - 19,41*1717,5 = 7676,08

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

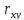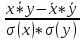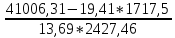= == 0,23

Линейный коэффициент корреляции принимает значения от –1 до +1.

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

0.1 < rxy < 0.3: слабая;

0.3 < rxy < 0.5: умеренная;

0.5 < rxy < 0.7: заметная;

0.7 < rxy < 0.9: высокая;

0.9 < rxy < 1: весьма высокая;

В нашем примере связь между признаком Y фактором X слабая и прямая.

Уравнение регрессии:

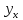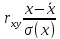
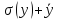= = 0,23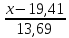2427,46 + 1717,5 = 40,95x + 922,72

Линейное уравнение регрессии имеет вид y = 40,95x + 922,72

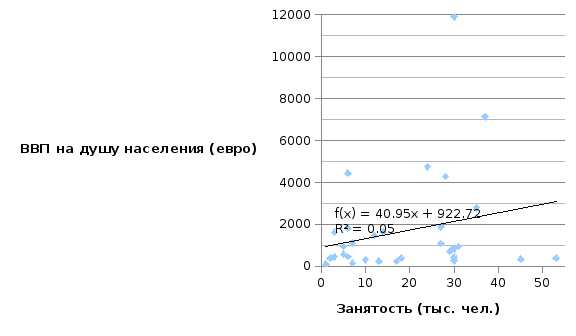
Рис. 3. Уровень регрессии

Таблица 7

Вспомогательная таблица расчетов

Страна
	y	x	y(x)	(y-y(x))2
Бельгия	436	30	2151.36	2942471.5
Болгария	446	3	1045.59	359505.41
Чехия	1102	7	1209.41	11536.12
Дания	1888	27	2028.5	19740.08
Германия	7128	37	2438.05	21995668.95
Эстония	156	7	1209.41	1109664.87
Ирландия	341	45	2765.68	5879088.58
Греция	1086	27	2028.5	888305.14
Испания	4738	24	1905.64	8022288.97
Франция	11896	30	2151.36	94957943
Италия	4287	28	2069.45	4917509.98
Кипр	946	31	2192.32	1553308.62
Латвия	248	13	1455.13	1457173.08
Литва	585	5	1127.5	294303
Люксембург	386	53	3093.32	7329583.91
Венгрия	1815	6	1168.45	418024.75
Нидерланды	266	30	2151.36	3554595.05
Австрия	835	30	2151.36	1732812.53
Польша	4438	6	1168.45	10689946.34
Португалия	226	17	1618.95	1940317.68
Румыния	1629	3	1045.59	340369.91
Словения	383	18	1659.91	1630492.81
Словакия	468	6	1168.45	490632.53
Финляндия	714	29	2110.41	1949957.31
Швеция	883	30	2151.36	1608745.64
Великобрит.	2791	35	2356.14	189106.14
Хорватия	385	2	1004.63	383945.11
Македония	106	1	963.68	735612.22
Турция	1634	14	1496.09	19019.47
Исландия	938	5	1127.5	35909.12
Норвегия	312	10	1332.27	1040951.44
Швейцария	1468	12	1414.18	2896.64
Сумма:	621	54960	54960	178501425.89

Эмпирическое корреляционное отношение:

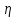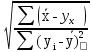= == 0,23

Где

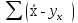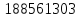= – 178501425,89 =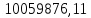

Для линейной регрессии индекс корреляции равен коэффициенту корреляции:

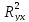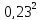= == 0,0529

Полученная величина свидетельствует о том, что фактор x не существенно влияет на y.

Оценим статистическую значимость уравнения регрессии в целом на пятипроцентном уровне с помощью F-критерия Фишера.

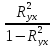= * (n-2) =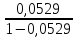* 30 = 1,676

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 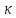₁ = 1 и 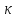₂ = 32-2 =30 составляет F_табл = 4,17.

Так как фактическое значение не превышает табличное, то уравнение регрессии признается статически незначимым на пятипроцентном уровне значимости.

Несмещенной оценкой дисперсии возмущений является величина:

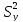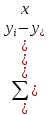= = 5950047.53 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

S_y = ==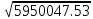2439.27

S_y = 2439.27 - стандартная ошибка оценки (стандартная ошибка регрессии). S_a - стандартное отклонение случайной величины a.

S_a = S_y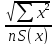

S_a = 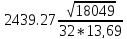= 748,03

S_b - стандартное отклонение случайной величины b.

S_b =

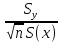
S_b = 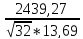= 31,5

Проверка гипотез относительно коэффициентов линейного уравнения регрессии.

t-статистика. Критерий Стьюдента.

t_крит (n-m-1;α/2) = (30;0.025) = 2.042

t_b = 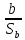==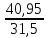 1,3

Поскольку 1.3 < 2.042, то статистическая значимость коэффициента регрессии b не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом b можно пренебречь.

t_a = 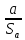==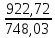 1,23

Поскольку 1.23 < 2.042, то статистическая значимость коэффициента регрессии a не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом a можно пренебречь.

Воспользуемся найденным ранее уравнением регрессии:

y_прогн = 922.72 + 40.95*120 = 6529.49

Доверительный интервал для зависимой переменной:

(b - t_крит Sb; b + t_крит Sb)

(40.95 - 2.042 • 31.5; 40.95 + 2.042 • 31.5)

(-23.36;105.27)

Т.е. (0; 105.27)

С вероятностью 95% можно гарантировать что значения при значении численности занятости населения в размере 120 тыс. чел. Значения ВВП будет находиться в интервале (0; 105.27) при неограниченно большом числе наблюдений.