
шпоры
.doc|
1. Системы линейных уравнений. x1, x2, …, xn а1x1 +а2x2 +…+аn xn = b k1, k2, …, kn x1 = k1, x2 = k2,…, xn = kn
Матрица системы столбец правых частей
Расширенная
матрица системы
Элементарные преобразования строк матрицы:
Преобразования обратимы. Система переходит в равносильную. Если получается строка расширенной матрицы, состоящая из нулей – ее вычеркивают.
|
2. Метод Гаусса. Метод Жордана.
п р я м о й х о д
о б р а т н ы й х о д Бывают системы, не имеющие решений (несовместные), имеющие ровно 1 решение (см. пример) и имеющие бесконечное число решений.
|
|
3 Действия над матрицами.
С=А+В, когда cij = aij + bij. Матрицы одного размера.
A+B=B+A,
В=k.А, когда bij = k.aij Получается матрица того же размера.
(km)A=k(mA),
1.A=A,
0.A=
Правило: «строка 1-й матрицы на столбец 2-й матрицы по формуле скалярного произведения». Число столбцов 1-й матрицы должно быть равно числу строк 2-й.
А
.
В = С
mxn nxp mxp скалярное произведение
Свойства.
1. (АВ)С=А(ВС) 2.
3.
5.
Транспонирование матриц – смена местами строк и столбцов.Свойства. 1. (АТ)Т=А 2. (А+В)Т=АТ+ВТ 3. (кА)Т=кАТ 4. (А.В)Т=ВТ.АТ
|
4 Обратная матрица.
Теорема. Пусть А,В,С – квадратные матрицы, причем А.В = Е, С.А = Е. Тогда В = С. В = Е.В = (С.А).В = С.(А.В) = С.Е = С Обратная матрица единственна и обозначается А-1 А.А-1 = А-1 .А = Е Матричная запись системы
Теорема. Если А – квадратная матрица, имеющая обратную А-1,то линейная система АХ=В имеет единственное решение при любых правых частях ( любом векторе В ) Х=А-1 .В Опр.
Если
Свойство.
Однородная система всегда совместна,
ее тривиальное решение
|
|
|
5.балансовая
модель Система уравнений материального баланса имеет вид
( Е – А )Х = У
Продуктивная
матрица:
Х = ( Е – А )-1У = SУ, S – матрица полных затрат
|
6. Свойства определителей. Определитель – число, характеризующее квадратную матрицу.
Для матрицы 1-го
порядка определитель
Система
Для матрицы 3-го
порядка
= а11.а22.а33 + а12.а23.а31 + а13.а21.а32 – а13.а22.а31 – а12.а21.а33 – а11.а23.а32
Всевозможные
произведения чисел из разных строк
и столбцов.Если из матрицы вычеркнуть
строки и столбцы так, что останется
квадратная матрица, то ее
определител.называется минором.
detA = a11 . A11 + a12 . A12 + …+ a1n . A1n Свойства.
1.
Независимость строк и столбцов
Следствия. 1. Если два столбца ( строки ) определителя совпадают, то он равен нулю.
Понижение порядка. Если в строке определителя все элементы, кроме одного, равны нулю, то при разложении по этой строке получается определитель меньшего ( на 1 ) порядка. Если
ранг матрицы системы линейных уравнений
меньше ранга ее расширенной матрицы,
то система несовместна.
|
||
|---|---|---|---|---|
|
|
|
|
||
|
7. Формулы Крамера.
Теорема 1.
Теорема 2.
Присоединенная (взаимная, союзная) матрица – из алгебраических дополнений транспонированная:
a11
.
A11+a12
.
A12+
…+a1n
.
A1n
=
Если
и т.д. – это числа из предыдущей матрицы.
|
8. Множества. Логическая символика.
аА аА АВ аА аВ А = В, если АВ и ВА 1) А = а1,а2,…ак перечисление элементов 2) А = хТ(х) с помощью свойства (формулы) АВ = ххА или хВ АВ = ххА и хВ А \ В = ххА, хВ
,
утверждения.
конъюнкция. дизъюнкция. хХ х квантор всеобщности хХ х квантор существования хХ х Операции над множествами Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Говорят,
что множество А содержится
в множестве В ( рис.1 )
или множество А является подмножеством множества В ( в
этом случае пишут А
Сумма
( объединение )
множеств А и В ( пишется А
Разность
множеств А и В ( пишется А – В ,
рис.3 )
есть множество элементов,
которые принадлежат множеству А , но не принадлежат
множеству В.Это множество называется также дополнением
множества В относительно множества А.
А \ В = ( А – В )
|
|
9. Функции вещественной переменной. D R x D f ( x ) E = yRy = f ( x ), x D f : D E y = f ( x )
f : D E x1,x2D x1 x2 f ( x1 ) f ( x2 ) yE xD : f ( x ) = y f-1 : E D x = f-1 ( y ) обратная функция
f : X Y, g : Y Z. Композиция ( сложная функция) h = g f : X Z h ( x ) = g ( f ( x ))
Элементарные функции. 1. y = xa, a R. 2. y = ax, a > 0, a 1. 3. y = logax, a > 0, a 1. 4. y = sin x, y = cos x, y = tg x, y = ctg x. 5. y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
x, y ) R2 x D, y = f ( x ) 11. Предел функции.
Пусть функция
«Замечательные» пределы:
1.
Свойства: Если
|
10. Предел последовательности вещественных чисел. Последовательность f : N R f ( n ) = xn– n-й член последовательности xn nN Число
а
называется пределом последовательности
xn
nN
(
>0 N: n> N xn a < Сходящаяся последовательность Геом. смысл. Вне интервала ( а , а + ) может находиться лишь конечное число xn Свойства.
Если
Последовательность:
Число
а
называется пределом последовательности
Сходящаяся последовательность. Геометрический смысл: Вне
интервала
Свойства: Если
Теорема
1 ( о сжатой
последовательности).Если
Теорема
2.Если
|


 размер m
x
n
размер m
x
n
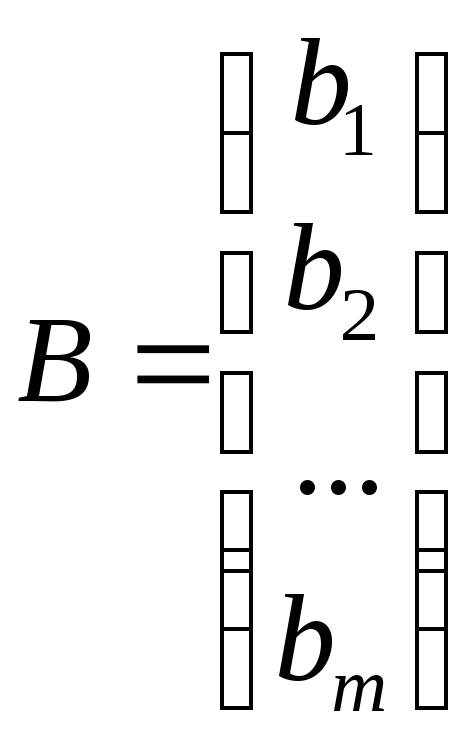 размер m
x
1
размер m
x
1
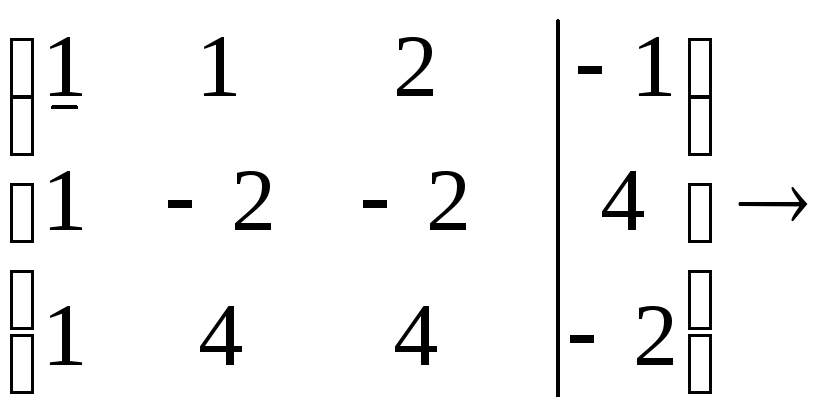

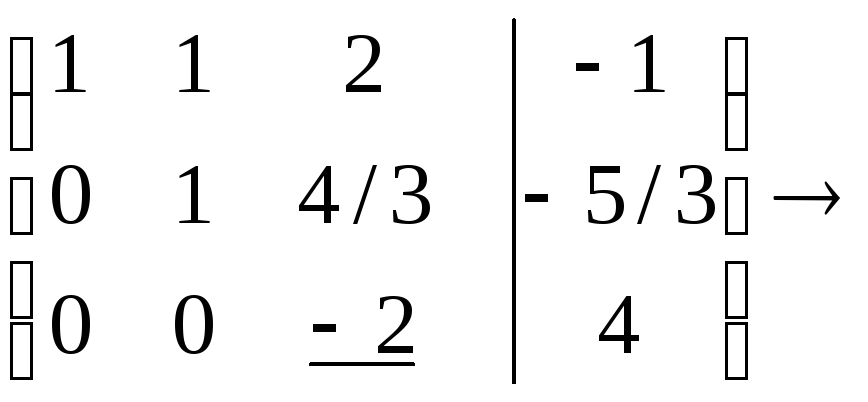

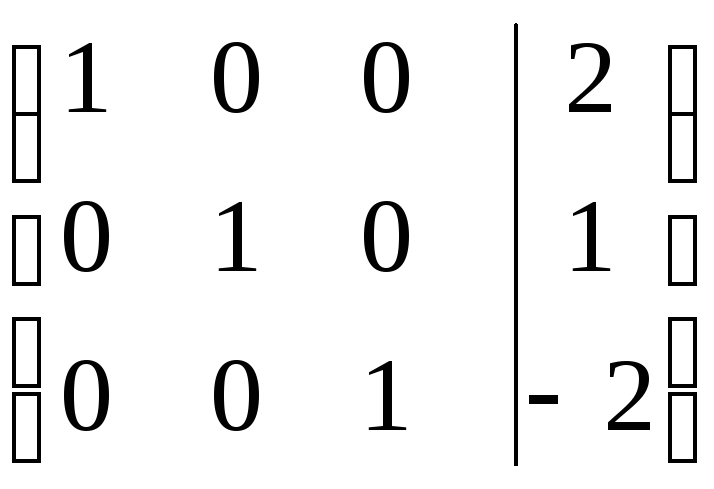
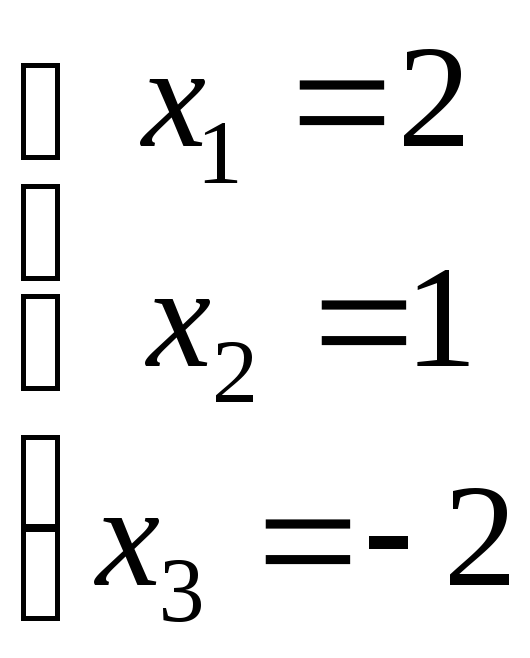
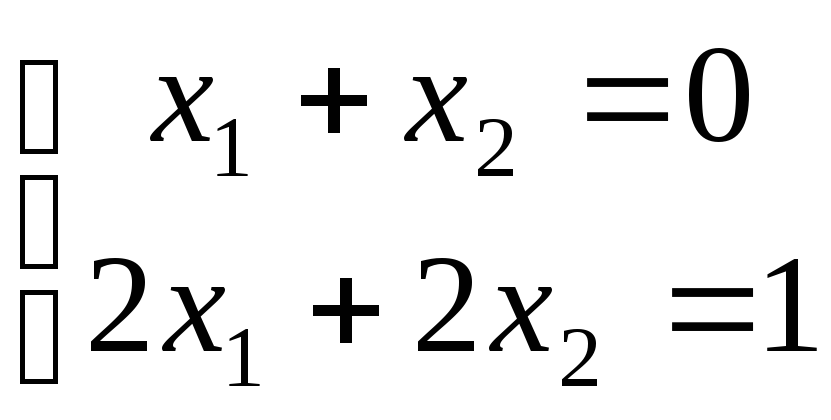 несовместная
несовместная
 имеет множество решений
имеет множество решений
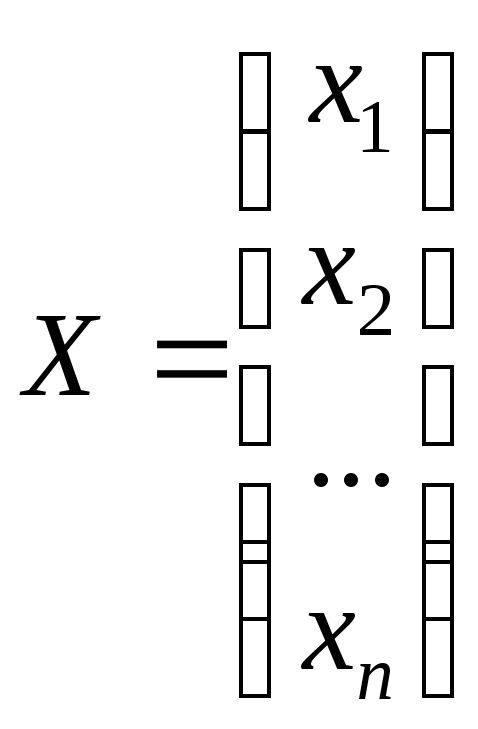
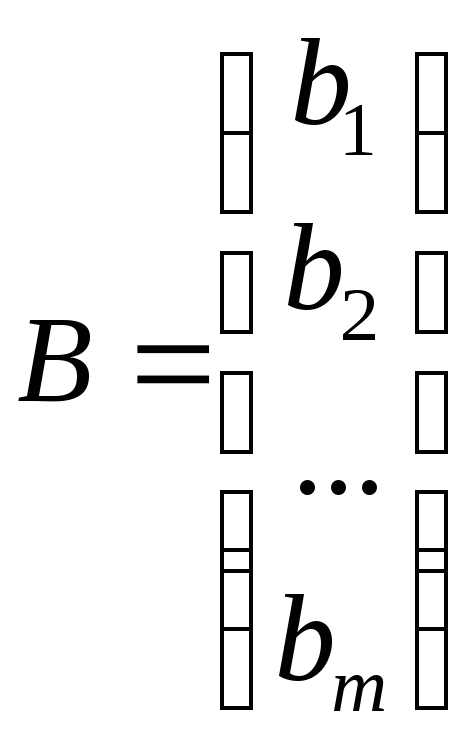 А.Х
= В
А.Х
= В

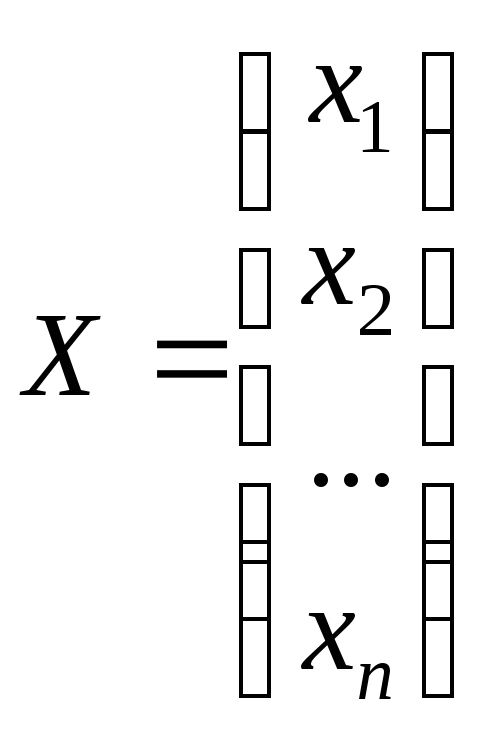 - валовая
продукция,
- валовая
продукция,
 - конечная продукция,
- конечная продукция,
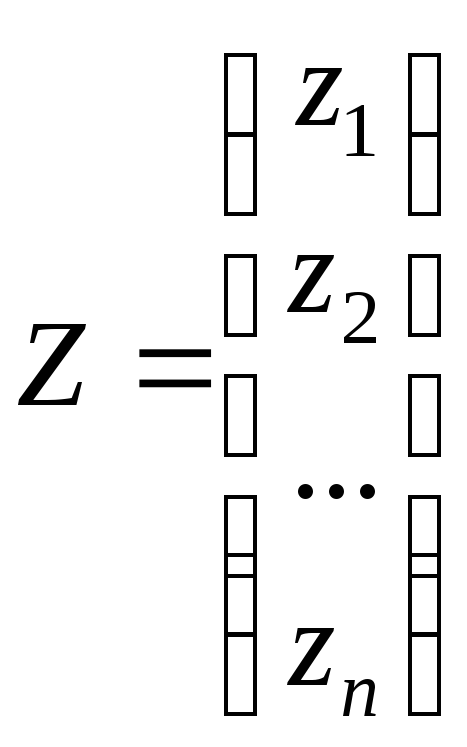 - внутренние затраты, которые зависят
от валовой продукции линейно:
z1=a11x1+a12x2+…+a1nxn
и т.д.
- внутренние затраты, которые зависят
от валовой продукции линейно:
z1=a11x1+a12x2+…+a1nxn
и т.д.
 Х –
АХ = У
балансовая модель Леонтьева
Х –
АХ = У
балансовая модель Леонтьева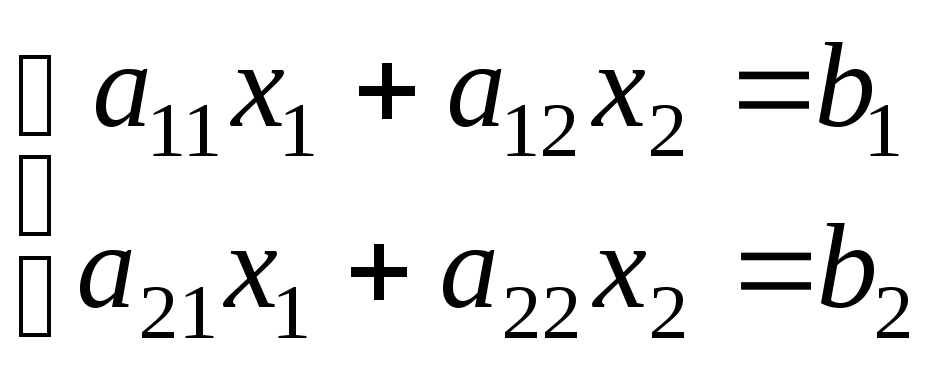 сводится к
сводится к

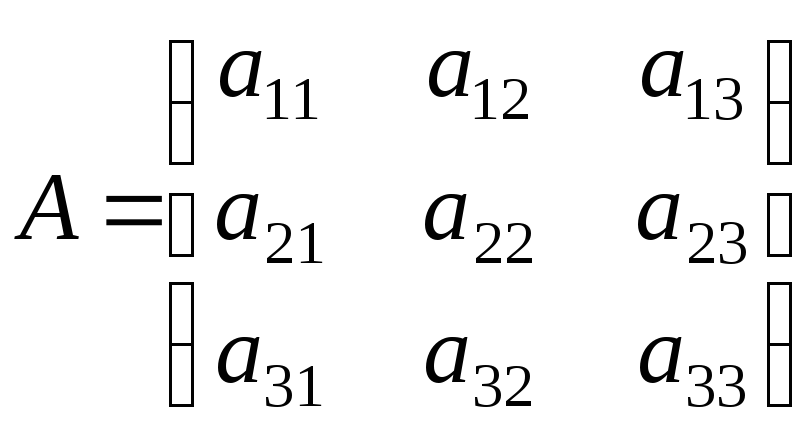 определитель
определитель
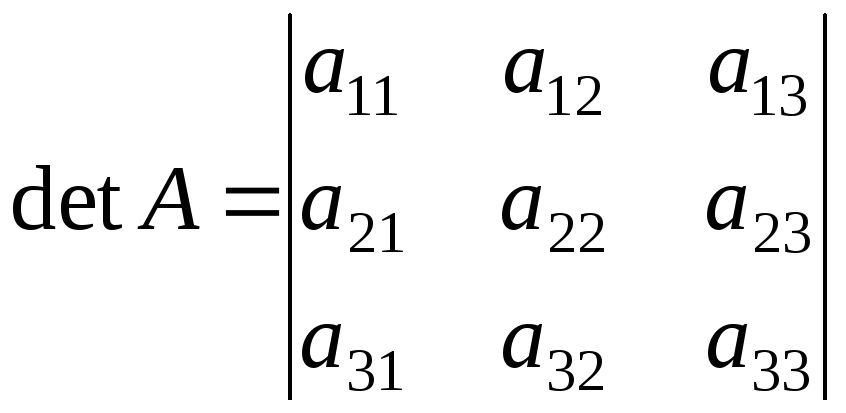 =
=
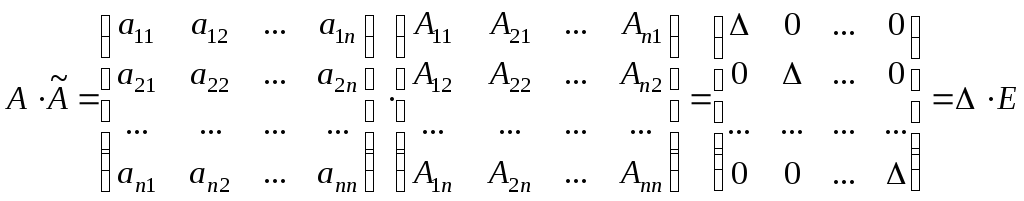
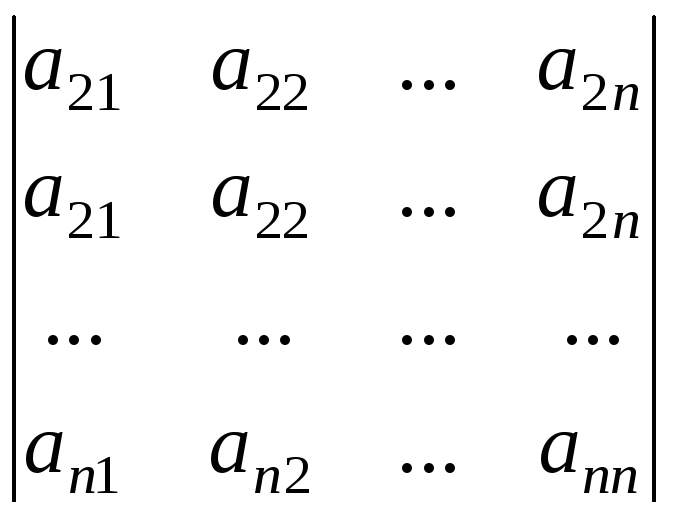 = 0
= 0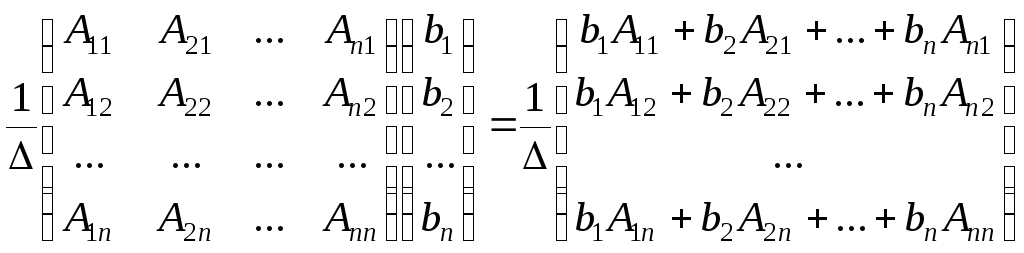
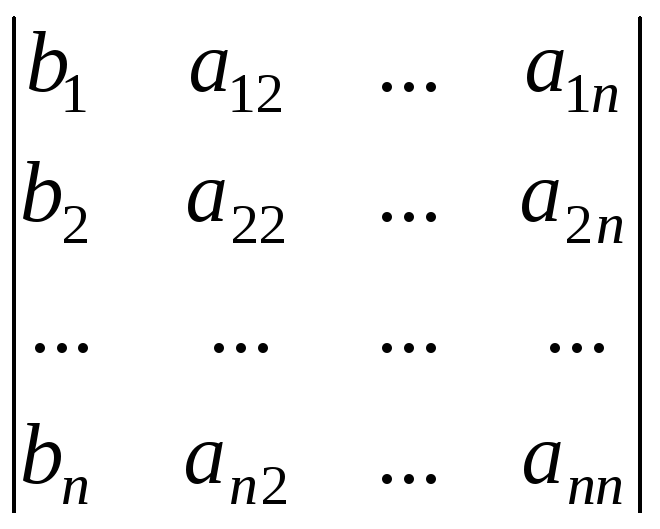 =b1A11
+b2A21+…
bnAn1=
=b1A11
+b2A21+…
bnAn1= =b1A12
+b2A22
+…+bnAn2
=
=b1A12
+b2A22
+…+bnAn2
= , то есть
, то есть

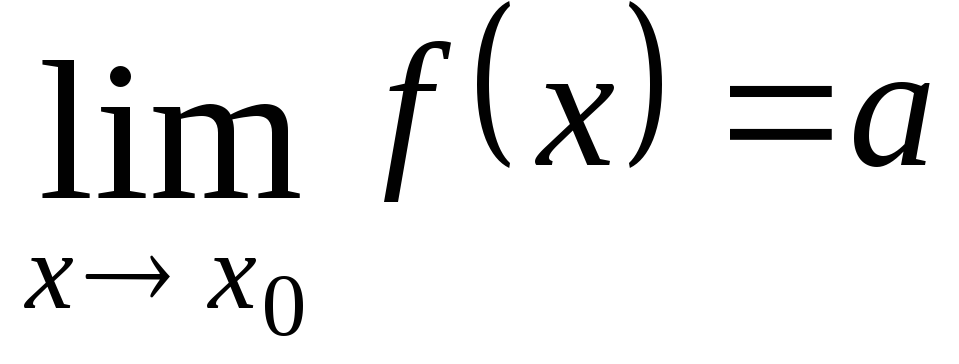 ),
если
),
если
 ,
то
,
то
