1. Классификация уравнений второго порядка

Линейные уравнения второго порядка в частных производных подразделяют на параболические,эллиптическиеигиперболические.

Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид:

где A, B, C — коэффициенты, зависящие от переменных x и y, а многоточие означает члены, зависящие от x, y, u и частных производных первого порядка: и. Это уравнение похоже на уравнениеконического сечения:

Так же, как конические сечения разделяются на эллипсы,параболыигиперболы, в зависимости от знакадискриминанта, классифицируются уравнения второго порядка в заданной точке:

1. —Гиперболическое уравнение,

2. —Эллиптическое уравнение,

3. —Параболическое уравнение(здесь предполагается, что в данной точке коэффициентыA, B, C не обращаются в нуль одновременно).

В случае, когда все коэффициенты A, B, C — постоянные, уравнение имеет один и тот же тип во всех точках плоскости переменных x и y. В случае, если коэффициенты A, B, Cнепрерывно зависят от x и y, множество точек, в которых данное уравнение относится к гиперболическому (эллиптическому), типу образует на плоскости открытую область, называемую гиперболической (эллиптической), а множество точек, в которых уравнение относится к параболическому типу, замкнуто. Уравнение называется смешанным (смешанного типа), если в некоторых точках плоскости оно гиперболическое, а в некоторых — эллиптическое. В этом случае параболические точки, как правило, образуют линию, называемую линией смены типа или линией вырождения.

В общем случае, когда уравнение второго порядка зависит от многих независимых переменных:

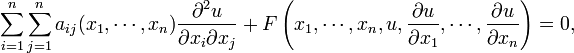
оно может быть далее классифицировано^[1] в заданной точке по аналогии с соответствующей квадратичной формой:

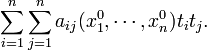
Невырожденным линейным преобразованием

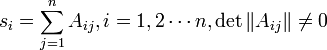
квадратичная форма всегда может быть приведена к каноническому виду:

При этом согласно теореме инерции число положительных, отрицательных и равных нулю коэффициентов в каноническом виде квадратичной формы является инвариантом и не зависит от линейного преобразования. На основе этого и производится классификация (в точке) рассматриваемого уравнения:

1. Если в точке 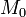квадратичная форма в каноническом виде имеет все коэффициенты одного знака, то уравнение в этой точке называется уравнениемэллиптического типа.

2. Если точке квадратичная форма в каноническом виде имеет коэффициенты различных знаков, но при этом все они отличны от 0, то уравнение в этой точке называется уравнениемгиперболического типа.

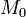3. Если точке квадратичная форма в каноническом виде имеет хотя бы один коэффициент равный 0, то уравнение в этой точке называется уравнениемпараболического типа.

В случае многих независимых переменных может быть проведена и более подробная классификация (необходимость которой в случае двух независимых переменных не возникает):

1. Гиперболический тип может быть дополнительно классифицирован на:

   1. Нормальный гиперболический тип, если один коэффициент одного знака, а остальные другого.

   2. Ультрагиперболический тип, если коэффициентов как одного знака так и другого более чем один.

2. Параболический тип может быть дополнительно классифицирован на:

   1. Эллиптически-параболический тип, если только один коэффициент равен нулю, а остальные имеют один знак.

   2. Гиперболически-параболический тип, если только один коэффициент равен нулю, а остальные имеют различные знаки. Аналогично гиперболическому типу он может быть разделён на:

      1. Нормальный гиперболически-параболический тип

      2. Ультрагиперболически-параболический тип

   3. Ультрапараболический тип, если более чем один коэффициент равен нулю. Здесь также возможна дальнейшая классификация в зависимости от знаков не равных нулю коэффициентов.