Типовой отчет

Найти решение краевой задачи для обыкновенного дифференциального уравнения второго порядка:

на отрезке [0, /2] со смешанными краевыми условиями

при a₀ = 1, a₁ = 2, b₀ = 3, b₁ = -1, A = 4, B = 6 методом прогонки с n = 10 и n = 20, по правилу Рунге оценить точность расчета при n = 20, сравнить решение с точным у_т = 2 sin x. Положив a₁ = b₁ = 0, вычислить коэффициенты А и В, найти решение полученной краевой задачи с краевыми условиями первого типа методом прогонки с n = 10 и n = 20, по правилу Рунге оценить точность расчета при n = 20, сравнить решение с точным.

Результаты решения краевой задачи со смешанными краевыми условиями при n = 10 и n = 20 представлены на рисунках. Максимальная ошибка при расчете исходной краевой задачи реализована при i = 0 для расчета с n = 10. Для расчета с n = 20 этому узлу также соответствует узел i = 0. Краевая задача со смешанными краевыми условиями имеет 1-ый порядок аппроксимации, поэтому прогноз ошибки по правилу Рунге производится по формуле: .

Проведем расчет для краевой задачи с краевыми условиями 1-го типа. Так как точное решение у = 2 sin x, то с учетом того, что по условию a₀ = 1, a₁ = 0, b₀ = 3, b₁ = 0, находим остальные константы граничных условий:

A = 12sin(0) = 0, B=32sin(/2) = 6.

Результаты решения краевой задачи с краевыми условиями 1-го типа при n = 10 и n = 20 представлены на рисунках. Максимальная ошибка при расчете исходной краевой задачи реализована при i = 4 для расчета с n = 10. Для расчета с n = 20 этому узлу также соответствует узел i = 8. Краевая задача со краевыми условиями 1-го типа имеет 2-ой порядок аппроксимации, поэтому прогноз ошибки по правилу Рунге производится по формуле: .

Результаты расчета функции в узлах с максимальными ошибкой для обеих сеток и задач с краевыми условиями (КУ) обоих типов, точные значения функции, прогноз ошибки в этих узлах по правилу Рунге и фактические значения ошибки приведены в таблице.

Задача	Смешанные КУ	КУ 1-го типа
y(h)	0,108638	1,175258
y(h/2)	0,059537	1,175494
yт	0	1,175571
d	0,049101	7,8710 -5
dф	0,059537	7,6210 -5

Прогнозные и фактические отклонения хорошо согласуются, что подтверждает правильность расчетов.

Варианты

Найти решение краевой задачи для обыкновенного дифференциального уравнения второго порядка:

на отрезке [a, b] со смешанными краевыми условиями

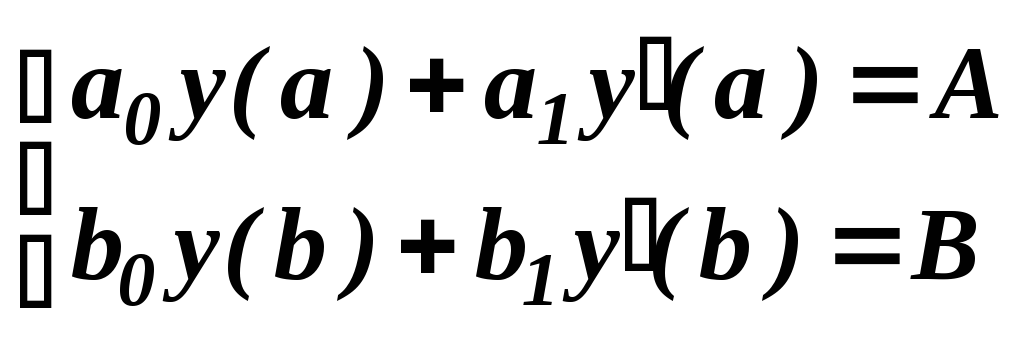
методом прогонки с n = 10 и n = 20, по правилу Рунге оценить точность расчета при n = 20, сравнить решение с точным у_т. Положив a₁ = b₁ = 0, вычислить коэффициенты А и В, найти решение полученной краевой задачи с краевыми условиями первого типа методом прогонки с n = 10 и n = 20, по правилу Рунге оценить точность расчета при n = 20, сравнить решение с точным.

1. p(x) = - x, q(x) = 4, g(x) = -2x sin 2x, y_т = cos 2x, x  [0, /2],

a₀ = 1, a₁ = 3, b₀ = 2, b₁ = -1, A = 1, B = -2

2. p(x) = 1/x, q(x) = x² , g(x) = 2x² ln x, y_т = 2 ln x, x  [1, e],

a₀ = 2, a₁ = 1, b₀ = -1, b₁ = e, A = 2, B = 0

3. p(x) = - x², q(x) = 3x , g(x) = 4x² +6x, y_т = x³+2x, x  [0, 1],

a₀ = 2, a₁ = -3, b₀ = 1, b₁ = 2, A = -6, B = 13

4. p(x) = - sin x, q(x) = cos x , g(x) = - 3 sin x, y_т = 3 sin x, x  [/2, ],

a₀ = 1, a₁ = 4, b₀ = -3, b₁ = 2, A = 3, B = -6

5. p(x) = 2/x, q(x) = - sin x , g(x) = - (2 sin x) /x, y_т = 2/x, x  [1, 2],

a₀ = 3, a₁ = -1, b₀ = - 2, b₁ = - 4, A = 8, B = 0

6. p(x) = 1/x, q(x) = - 1/x² , g(x) = -( 2 ln x)/x², y_т = 2 ln x - x, x  [1, 2],

a₀ = 1, a₁ = -e, b₀ = - 1, b₁ = e², A = 0, B =-2

7. p(x) = 2x, q(x) = - 2x cos x , g(x) = - sin x – x sin 2x, y_т = sin x + 1,

x  [0, /2], a₀ = 3, a₁ = 2, b₀ = - 1, b₁ = -2, A = 5, B =-2

8. p(x) = ln 2x, q(x) = - 1/x , g(x) = -1/x², y_т = ln 2x, x  [1/2, e/2],

a₀ = 4, a₁ = -1, b₀ = - 3, b₁ = e, A = - 2, B = - 1

9. p(x) = sin x, q(x) = - 6/x² , g(x) = -(2 sin x)/x³, y_т = 1/x², x  [1, 2],

a₀ =2, a₁ = 1, b₀ = 4, b₁ = 8, A = 0, B = - 1

10. p(x) = x, q(x) = 1 , g(x) = 1-2x sin x, y_т = 2cos x + 1, x  [/2, ],

a₀ =2, a₁ = 1, b₀ = 4, b₁ = 8, A = 0, B = - 1

11. p(x) = x, q(x) = 4 , g(x) = 2x cos 2x, y_т = sin2x, x  [0, ],

a₀ =1, a₁ = 2, b₀ = 1, b₁ = 1, A = 4, B = 2

12. p(x) = -x² , q(x) = 2x , g(x) = 2(x + 1), y_т = x² + 1, x  [0, 1],

a₀ =1, a₁ = 2, b₀ = 1, b₁ = -1, A = 1, B = 0

13. p(x) = cos x , q(x) = -sin x , g(x) = - (cos x + sin x) , y_т = cos x + 1,

x  [0, /2], a₀ =1, a₁ = 2, b₀ = 1, b₁ = 1, A = 2, B = 0

14. p(x) = x cos 2x , q(x) = 2x sin 2x , g(x) = - 4 cos 2x , y_т = cos 2x,

x  [0, /2], a₀ =3, a₁ = 1, b₀ = 1, b₁ = 2, A = 3, B = - 1

15. p(x) = ln x , q(x) = -1/x , g(x) = - 2/x² , y_т = 2 ln x, x  [1, e],

a₀ =1, a₁ = - 1, b₀ = - 1, b₁ = e, A = - 2, B = 0

16. p(x) = - x , q(x) = 3 , g(x) = 12x , y_т = x³ + 2x, x  [0, 1],

a₀ =1, a₁ = - 1, b₀ = 1, b₁ = - 1, A = - 2, B = -2

17. p(x) = x sin x , q(x) = - x cos x , g(x) = -2 sin x , y_т = 2 sin x,

x  [0, /2], a₀ =2, a₁ = 1, b₀ = 1, b₁ = 2, A = 2, B = 2

18. p(x) = sin x , q(x) = sin x / x , g(x) = 6 / x³ , y_т = 3 / x, x  [1, 3],

a₀ =1, a₁ = 2, b₀ = 1, b₁ = 9, A = -3, B = 0

19. p(x) = 1 / x , q(x) = - 1 / x² , g(x) = 1 – 4x² , y_т = ln x – 2x, x  [1, e],

a₀ = - 2, a₁ = 1, b₀ = 1, b₁ = 2e², A = 3, B = 1 – 4e²

20. p(x) = x² sin x , q(x) = - x² cos x , g(x = x² cos x – sin x , y_т = sin x -1,

x  [/2, ], a₀ = 1, a₁ = 3, b₀ = 1, b₁ = - 2, A = 0, B = 1

21. p(x) = x ln 2x , q(x) = -1 , g(x) = – 1 / x² , y_т = ln 2x, x  [1/2, e/2],

a₀ = 1, a₁ = 3, b₀ = - 1, b₁ = e, A = 6, B = 1

22. p(x) = 3 / x, q(x) = sin x , g(x) = (sin x) / x² , y_т = 1 / x², x  [1, 2],

a₀ = 1, a₁ = - 2, b₀ = 1, b₁ = 1, A = 5, B = 0

23. p(x) = x cos x, q(x) = x sin x , g(x) = - 3 cos x+2x sin x, y_т=3cos x+2,

x  [0, /2], a₀ = 1, a₁ = 2, b₀ = - 1, b₁ = 1, A = 5, B = - 5

24. p(x) = - 2x³, q(x) = 4x, g(x) = 4( x + 1), y_т = 2x² + 1, x  [0, 1],

a₀ = 2, a₁ = - 1, b₀ = - 1, b₁ = 1, A = 2, B = 1