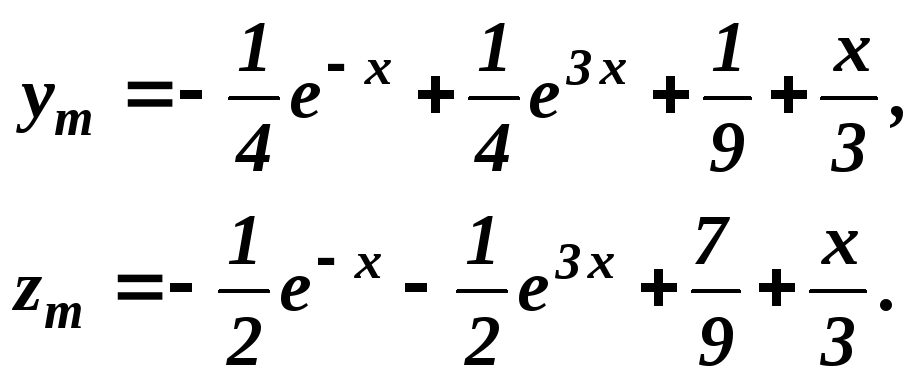Типовой отчет.

Задание 1. Найти решение задачи Коши для системы двух обыкновенных дифференциального уравнений первого порядка:

с начальными условиями y(1) = 0, z(1) = 2 на отрезке x  [1; 2] на сетке с числом шагов m = 5 и m = 10, оценить по правилу Рунге точность расчетов и сравнить с точным решением .

Используется следующий алгоритм решения системы двух обыкновенных дифференциальных уравнений методом Рунге-Кутта четвертого порядка:

,

,

,

,

,

,

,

,

.

Практическую оценку погрешности решения, найденного на сетке с шагом 0,1 производим с помощью приближенного правила Рунге, учитывая, что используемый метод имеет четвертый порядок точности:

.

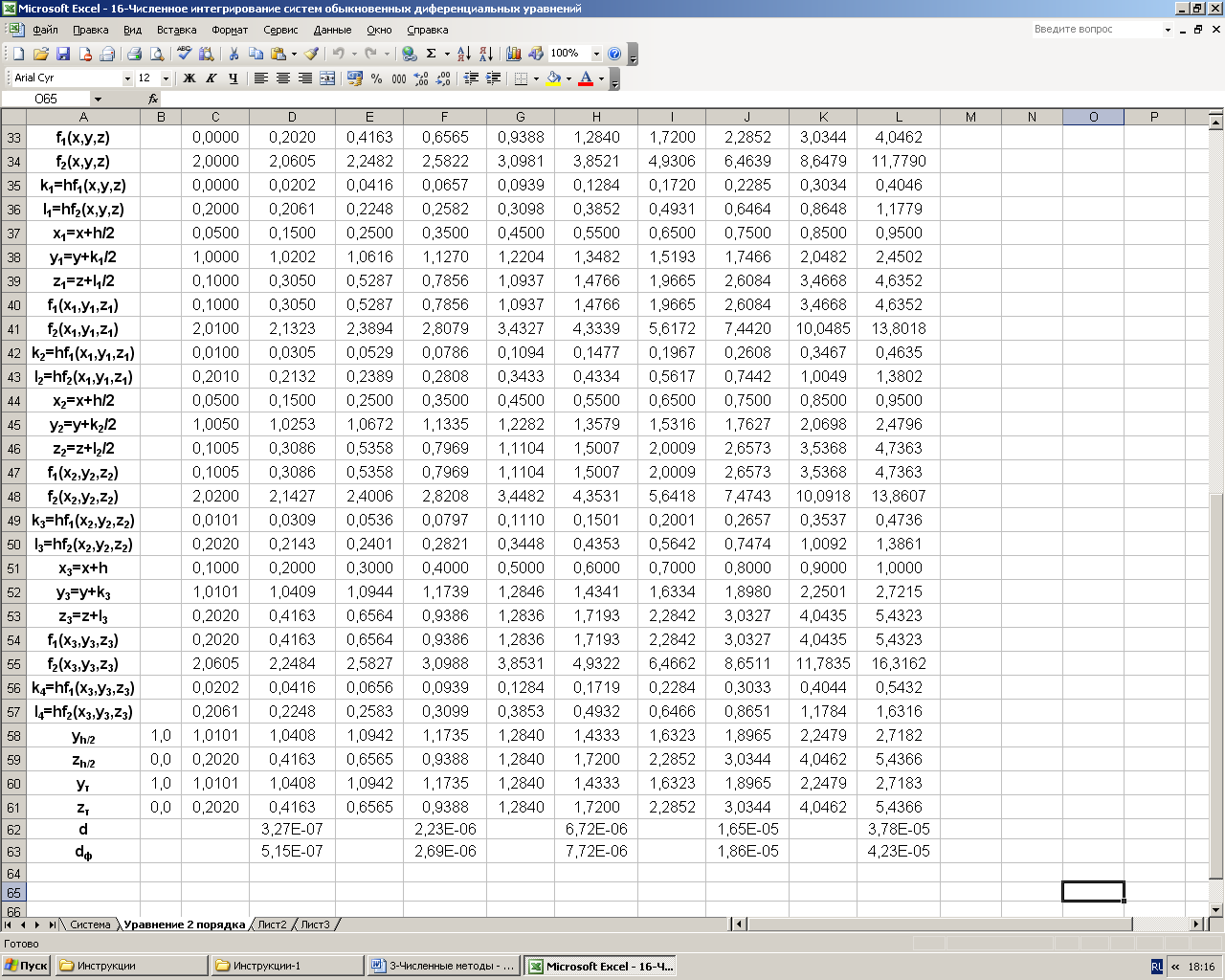
Результаты расчетов приведены в таблице (см. рисунок).

Задание 2. Задачу Коши для дифференциального уравнения

преобразовать к задаче Коши для системы двух дифференциальных уравнений первого порядка и решить с помощью разработанного расчетного листа, внеся в него соответствующие изменения. Точное решение .

Преобразуем уравнение к задаче Коши для системы двух дифференциальных уравнений первого порядка, используя обозначения предыдущего примера:

y(0) = 1, z(0) = 0.

Точное значение функции z получено дифференцированием функции у: .

Решение выполняется потому же алгоритму, что и в первом задании.

Результаты расчетов приведены в таблице (см. рисунок).

Варианты

Задание 1. Найти решение задачи Коши для системы двух обыкновенных дифференциального уравнений первого порядка с заданными начальными условиями y(х₀ ) = у₀ , z(x₀ ) = z₀ на отрезке x  [a; b] на сетке с числом шагов m = 5 и m = 10, оценить по правилу Рунге точность расчетов и сравнить с точным решением .

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

Задание 2. Задачу Коши для данного дифференциального уравнения второго порядка преобразовать к задаче Коши для системы двух дифференциальных уравнений первого порядка. Найти решение системы классическим методом Рунге-Кутта на сетке отрезка [a, b] с шагами h = 0,2 и h/2 = 0,1. Оценить погрешность численного решения по правилу Рунге. Сравнить численное решение с известным аналитическим решением.

1. .

2. .

3. .

4. .

5. .

6.

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

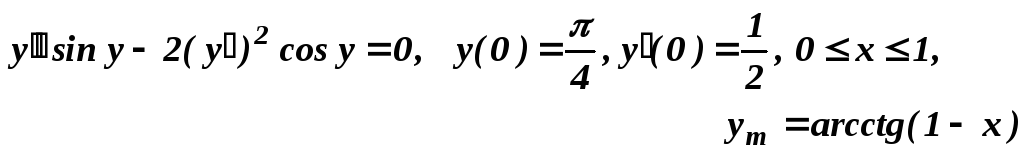24. .

Вид рабочего листа Excel

Лабораторная работа № 17

"Решение краевой задачи для обыкновенного дифференциального

уравнения второго порядка"

Элементы теории

Краевая задача для обыкновенного дифференциального уравнения второго порядка формулируется следующим образом. Требуется найти функцию y=y(x), которая внутри отрезка [a, b] удовлетворяет уравнению

, (1)

ана концах отрезка – краевым условиям:

(2)

Пусть краевые условия имеют вид:у(а) = А, у(b) = B. Тогда геометрически решение уравнения (1) представляет собой интегральную кривую y=y(x), проходящую через заданные точки M(a, A) и N(b, B).

Пусть теперь для уравнения (1) известны значения производных искомой функции в граничных точках у (а) = А₁ , у (b) = B₁ . Тогда геометрически решение уравнения (1) представляет собой интегральную кривую y=с, которая пересекает прямые x = a и y = b соответственно под углами  = arctg A₁ и  = arctg B₁ .

Если для уравнения (1) в одной граничной точке известно значение искомой функцииу(а) = А, а в другой – значение производной функции у (b) = B₁ , то такая краевая задача называется смешанной. Геометрически решение уравнения (1) означает, что надо найти интегральную кривую y=y(x), которая проходит через точку M(a, A) и пересекает прямую и y = b под углом  = arctg B₁ .

Если дифференциальное уравнение и краевые условия линейны, то такая задача называется линейной. В этом случае дифференциальное уравнение и краевые условия имеют вид:

(3)

(4)

где p(x), q(x), g(x) – известные непрерывные функции на отрезке [a, b] функции, a₀ , a₁ , b₀ , b₁ , A, B – заданные постоянные, причем ,. Еслиf(x) = 0 при a  x  b, то уравнение называется однородным, а в противном случае – неоднородным. Если А = В = 0, то соответствующее краевое условие называется однороднымаевое условим, а в противном случае - неоднородным. точках 0000000000000000000000000000000000000. Если и дифференциальное уравнение и краевые условия однородны, то краевая задача называется однородной.

К задаче (3)-(4) могут быть сведены некоторые задачи стационарной теплопроводности и диффузии..

Рассмотрим краевую задачу (3)-(4). Пусть x₀ = a, x_n = b, x_i = x₀ + ih, i = 1, 2, … , n-1 – система равноотстоящих узлов с некоторым шагом h = (b – a)/n и p_i=p(x_i), q_i=q(x_i), g_i=g(x_i). Полученные в результате расчета приближенные значения искомой функции у(х) и ее производных у(х), у(х) в узлах x_i обозначим соответственно y_i , . Аппроксимируем производные во внутренних узлах сетки со вторым порядком точности:

, (5)

а для концевых точек x₀ = a, x_n = b – с первым порядком:

. (6)

Подставляя аппроксимации (5)-(6) в краевую задачу (3)-(4), после преобразований получим:

(7)

(8)

Полученная разностная схема имеет в общем случае первый порядок аппроксимации из-за необходимости использовать формулы (6) в краевых точках. Но если используются краевые условия первого типа (a₁ = 0 и b₁ =0), то аппроксимации (6) в разностной схеме (7)-(8) не участвуют и порядок точности повышается до второго.

Введем обозначения:

(9)

. (10)

Тогда разностная схема (7)-(8) переходит в приведенную форму:

(11)

Система (11) представляет собой систему линейных алгебраических уравнений с трехдиагональной матрицей размера (N-1) (N-1):

Для решения краевой задачи (11) можно использовать вариант метода исключения, называемый методом прогонки. Предполагается, что имеет место соотношение:

(12)

Для определения неизвестных коэффициентов _i+1 и _i+1 соотношение (12) подставляется в систему (11) и из сравнения сомножителей при одинаковых значениях функции y_i получают необходимые выражения.

Алгоритм метода состоит из двух шагов:

а) в прямой прогонке вычисляются значения коэффициентов _i+1 и _i+1 :

(13)

(14)

(15)

(16)

б) в обратной прогонке вычисляются искомые значения функции y_i :

(17)

(18)

Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке x_i  [a, b] производят с помощью приближенного равенства - правила Рунге:

, (19)

где р – порядок точности численного метода. Таким образом, оценка полученного результата по формуле (19) вынуждает проводить вычисления дважды: один раз с шагом h, другой – с шагом h/2. Порядок точности р = 1 для краевой задачи с краевыми условиями 2-го и 3-го типов и р = 2 для краевой задачи с краевыми условиями 1-го типа.