Порядок выполнения лабораторной работы.

Пример 1. Найти решение задачи Коши для системы двух обыкновенных дифференциального уравнений первого порядка:

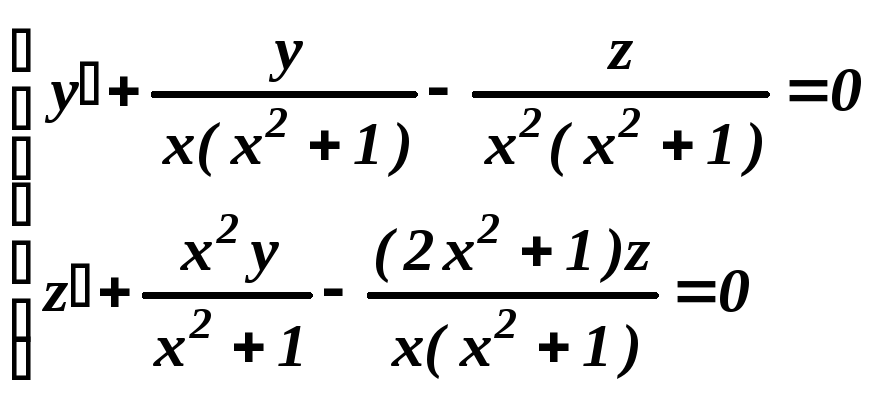
с начальными условиями y(1) = 0, z(1) = 2 на отрезке x  [1; 2] на сетке с числом шагов m = 5 и m = 10, оценить по правилу Рунге точность расчетов и сравнить с точным решением .

Перед началом вычислений преобразуем систему уравнений:

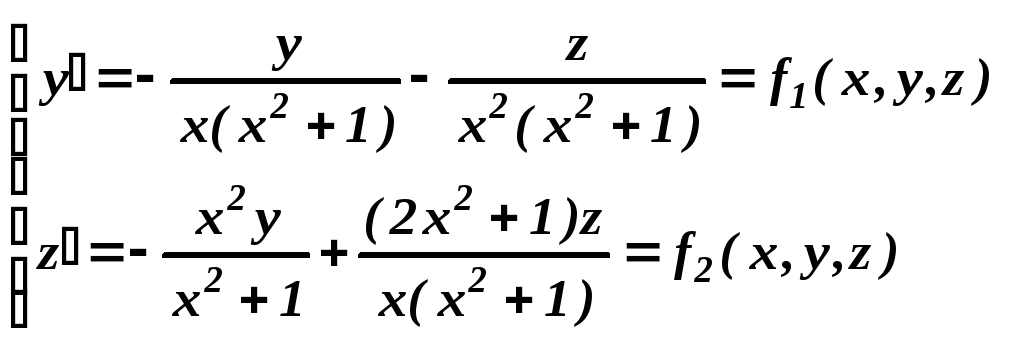
Вид рабочего листа табличного процессора MS Excel приведен на рисунке. Оформление расчетов аналогично лабораторной работе "Численное интегрирование обыкновенного дифференциального уравнения первого порядка" для метода Рунге-Кутта. Отличие связано с появлением дополнительных строк для второго уравнения.

В диапазоне A5:A63 размещаем заголовки строк. Задаем узловые точки сетки: В5="1", С5="1.1", протягиваем диапазон В5:С5 до ячейки L5.

Программируем рабочий лист для вычислений с шагом h=0,2. Размещаем начальное условие y(1) = 0, z(1) = 2: ячейка В31="0", В32="2". Проводим расчет в 1-ой узловой точке. Вычисляем угловой коэффициент функции у в начальной точке : ячейкаD6 ="=-B31/B5/(B5^2+1)+B32/(B5^2)/(B5^2+1)". Вычисляем угловой коэффициент функции z в начальной точке : ячейкаD7="=-(B5^2)*B31/(B5^2+1)+(2*B5^2+1)*B32/B5/(B5^2+1)". Вычисляем коэффициент : ячейкаD8="=(D5-B5)*D6". Вычисляем коэффициент : ячейкаD9="=(D5-B5)*D7".

Вычисляем аргументы коэффициентов k₂ и l₂: ячейка D10="=B5+(D5-B5)/2" (), ячейкаD11="=B31+D8/2" (y₀ + k₁/2 ), ячейка D12=" =B32+D9/2" (z₀ + l₁/2 ) . Вычисляем функцию f₁ от полученных аргументов: ячейка D13="=-D11/D10/(D10^2+1)+D12/D10^2 /(D10^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка D14="=-(D10^2)*D11/(D10^2+1)+(2*D10^2+1) *D12/D10/(D10^2+1)". Вычисляем коэффициент k₂=hf₁: ячейка D15="=(D5-B5)*D13". Вычисляем коэффициент l₂=hf₂: ячейка D16="=(D5-B5)*D14".

Вычисляем аргументы коэффициентов k₃ и l₃: ячейка D17=" =B5+(D5-B5)/2" (), ячейкаD18=" =B31+D15/2" (y₀ + k₂/2 ), ячейка D19= "=B32+D16/2" (z₀ + l₂/2) . Вычисляем функцию f₁ от полученных аргументов: ячейка D20= "=-D18/D17/(D17^2+1)+D19/D17^2/ (D17^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка D21= "=-(D17^2)*D18/(D17^2+1)+(2*D17^2+1)*D19/D17/(D17^2+1)". Вычисляем коэффициент k₃=hf₁: ячейка D22="=(D5-B5)*D20". Вычисляем коэффициент l₃=hf₂: ячейка D23=" =(D5-B5)*D21".

Вычисляем аргументы коэффициентов k₄ и l₄: ячейка D24="=D5" (), ячейкаD25="=B31+D22" (y₀ + k₃ ), ячейка D26="=B32+D23" (z₀ + l₃). Вычисляем функцию f₁ от полученных аргументов: ячейка D27= "=-D25/D24/(D24^2+1)+D26/D24^2/(D24^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка D28="=-(D24^2)*D25/(D24^2+1) +(2*D24^2+1)*D26/D24/(D24^2+1)". Вычисляем коэффициент k₄=hf₁: ячейка D29="=(D5-B5)*D27". Вычисляем коэффициент l₄=hf₂: ячейка D30="=(D5-B5)*D28". Вычисляем следующее приближенное значение функции у₁ = у₀ + (k₁ + 2k₂ + 2k₃ + k₄ )/6 : ячейка D31="=B31+(D8+2*D15+2*D22+D29)/6". Вычисляем следующее приближенное значение функции z₁ = z₀ + (l₁ + 2l₂ + 2l₃ + l₄ )/6 : ячейка D32="=B32+(D9+2*D16+2*D23+D30)/6". Протягиваем диапазон D6:E32 в диапазон D6:L32 для вычислений в остальных узловых точках.

Программируем рабочий лист для вычислений с шагом h=0,1. Размещаем начальное условие y(1) = 0, z(1) = 2: ячейка В58="0", В59="2". Проводим расчет в 1-ой узловой точке. Вычисляем угловой коэффициент функции у в начальной точке : ячейкаC33="=-B58/B5/(B5^2+1)+B59/B5^2/(B5^2+1)". Вычисляем угловой коэффициент функции z в начальной точке : ячейкаC34="=-(B5^2)*B58/(B5^2+1)+(2*B5^2+1)*B59/B5/(B5^2+1)". Вычисляем коэффициент : ячейкаC35="=(C5-B5)*C33". Вычисляем коэффициент : ячейкаC36="=(C5-B5)*C34".

Вычисляем аргументы коэффициентов k₂ и l₂: ячейка C37= "=B5+(C5-B5)/2" (), ячейкаC38="=B58+C35/2" (y₀ + k₁/2 ), ячейка C39="=B59+C36/2" (z₀ + l₁/2 ) . Вычисляем функцию f₁ от полученных аргументов: ячейка C40="=-C38/C37/(C37^2+1)+C39/C37^2/(C37^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка C41= "=-(C37^2)*C38/(C37^2+1)+(2*C37^2+1)*C39/C37/(C37^2+1)". Вычисляем коэффициент k₂=hf₁: ячейка C42="=(C5-B5)*C40". Вычисляем коэффициент l₂=hf₂: ячейка C43="=(C5-B5)*C41".

Вычисляем аргументы коэффициентов k₃ и l₃: ячейка C44= "=B5+(C5-B5)/2" (), ячейкаC45="=B58+C42/2" (y₀ + k₂/2 ), ячейка C46="=B59+C43/2" (z₀ + l₂/2) . Вычисляем функцию f₁ от полученных аргументов: ячейка C47="=-C45/C44/(C44^2+1)+C46/C44^2/(C44^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка C48= "=-(C44^2)*C45/(C44^2+1)+(2*C44^2+1)*C46/C44/(C44^2+1)". Вычисляем коэффициент k₃=hf₁: ячейка C49="=(C5-B5)*C47". Вычисляем коэффициент l₃=hf₂: ячейка C50="=(C5-B5)*C48".

Вычисляем аргументы коэффициентов k₄ и l₄: ячейка C51="=C5" (), ячейкаC52="=B58+C49" (y₀ + k₃ ), ячейка C53="=B59+C50" (z₀ + l₃). Вычисляем функцию f₁ от полученных аргументов: ячейка C54= "=-C52/C51/(C51^2+1)+C53/C51^2/(C51^2+1)". Вычисляем функцию f₂ от полученных аргументов: ячейка C55="=-(C51^2)*C52/(C51^2+1)+ (2*C51^2+1)*C53/C51/(C51^2+1)". Вычисляем коэффициент k₄=hf₁: ячейка C56="=(C5-B5)*C54". Вычисляем коэффициент l₄=hf₂: ячейка C57="=(C5-B5)*C55". Вычисляем следующее приближенное значение функции у₁ = у₀ + (k₁ + 2k₂ + 2k₃ + k₄ )/6 : ячейка C58="=B58+(C35+2*C42+2*C49+C56)/6". Вычисляем следующее приближенное значение функции z₁ = z₀ + (l₁ + 2l₂ + 2l₃ + l₄ )/6 : ячейка C59="=B59+(C36+2*C43+2*C50+C57)/6". Протягиваем диапазон C33:C59 в диапазон D33:L59 для вычислений в остальных узловых точках.

Вычисляем точное значение функции в узловых точках: ячейкаВ60="=1-1/B5" и протягиваем формулу в диапазон B60:L60. Вычисляем точное значение функции z_т = x + x² в узловых точках: ячейка В61="=B5+B5^2" и протягиваем формулу в диапазон B61:L61. По формуле (7) вычисляем оценку точности в узловых точках более крупной сетки: ячейка D62="=МАКС(ABS(D58-D31);ABS(D59-D32))/15" и протягиваем диапазон D62:E62 до ячейки L62. По формуле (6) вычисляем фактическое отклонение приближенного значения на сетке h/2 в узлах более крупной сетки: ячейка D63=" =МАКС(ABS(D58-D60);ABS(D59-D61))" и протягиваем диапазон D63:E63 до ячейки L63. Вычисления по классическому методу Рунге-Кутта закончены.

Пример 2. Задачу Коши для дифференциального уравнения

преобразовать к задаче Коши для системы двух дифференциальных уравнений первого порядка и решить с помощью разработанного расчетного листа, внеся в него соответствующие изменения. Точное решение .

Преобразуем уравнение к задаче Коши для системы двух дифференциальных уравнений первого порядка, используя обозначения предыдущего примера:

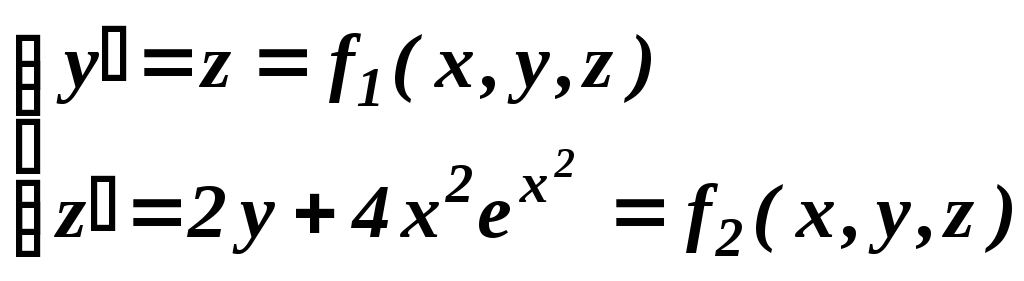
y(0) = 1, z(0) = 0.

По сравнению с предыдущим примером на рабочий лист внесены следующие изменения. Изменен диапазон интегрирования на отрезок [0; 1]. Изменены формулы в строках, в которых вычисляются функции f₁ и f₂ . Изменено точное вычисление функции у в строке 60. Точное значение функции z (строка 61) получено дифференцированием функции у: . Остальные вычисления проводятся автоматически. Вид рабочего листа табличного процессораMS Excel приведен на рисунке.