Типовой отчет.

Найти решение задачи Коши для дифференциального уравнения первого порядка с начальным условиемна равномерной сетке отрезка[0; 1] один раз с шагом h = 0,2 , другой – с шагом 0,1 методами Эйлера, Эйлера-Коши и классическим методом Рунге-Кутта. Оценить погрешность численного решения по принципу Рунге. Сравнить численное решение с точным (x) = 2e ^x – x - 1.

1. Метод Эйлера. Используется алгоритм

.

Практическую оценку погрешности решения, найденного на сетке с шагом 0,1 производим с помощью приближенного правила Рунге:

.

Результаты расчетов приведены в таблице (см. рисунок).

2. Метод Эйлера-Коши. Используется алгоритм:

.

Практическую оценку погрешности решения, найденного на сетке с шагом 0,1 производим с помощью приближенного правила Рунге:

.

Результаты расчетов приведены в таблице (см. рисунок).

3. Классический метод Рунге-Кутта. Используется алгоритм:

,

,

,

,

.

Практическую оценку погрешности решения, найденного на сетке с шагом 0,1 производим с помощью приближенного правила Рунге:

.

Результаты расчетов приведены в таблице (см. рисунок).

Варианты

Найти решение задачи Коши для дифференциального уравнения первого порядка с заданным начальным условием на равномерной сетке отрезка[a; b] один раз с шагом h = 0,2 , другой – с шагом 0,1 методами Эйлера, Эйлера-Коши и классическим методом Рунге-Кутта. Оценить погрешность численного решения по принципу Рунге. Сравнить численное решение с точным (x).

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

Вид рабочего листа Excel

Лабораторная работа № 16

"Численное интегрирование систем обыкновенных дифференциальных

уравнений первого порядка"

Элементы теории

Пусть дана система двух дифференциальных уравнений первого порядка:

(1)

Решением системы (1) называется пара функций ₁(х) и ₂(х), при подстановке которых в систему получаются тождества:

.

Решению 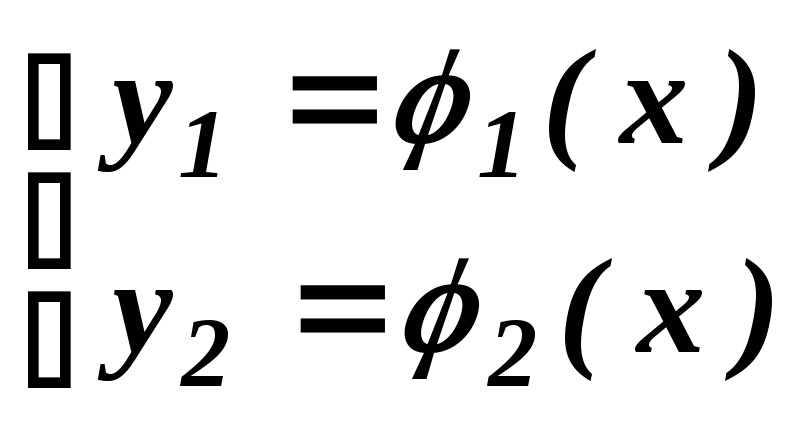системы уравнений (1) соответствует интегральная кривая в пространстве трех измерений(x, y, z). Условия, при которых через каждую точку P₀ (x₀ , y₀ , z₀ ) некоторой области D трехмерного пространства проходит единственная интегральная кривая, содержатся в теореме существования и единственности решения.

Теорема. Если функции f₁ (x, y, z) и f₂ (x, y, z) – правые части дифференциальных уравнений системы (1) – непрерывны вместе со своими частными производными по переменным y и z в некоторой области D трехмерного пространства, то для любой точки (x₀ , y₀ , z₀ ) D система (1) имеет единственное решение, удовлетворяющее начальным условиям:

y(x₀ ) = y₀ , z(x₀ ) = z₀ . (2)

Задача Коши состоит в нахождении решения системы (1), удовлетворяющего начальным условиям (2).

Постановка задачи Коши для системы n дифференциальных уравнений первого порядка аналогична задаче (1)-(2), а именно, требуется найти решение системы:

(3)

при начальных условиях

y₁ (x₀ ) = y₁₀ , y₂ (x₀ ) = y₂₀ , … , y_n (x₀ ) = y_n0 . (4)

Теорема существования и единственности решения задачи Коши (3)-(4) имеет формулировку, аналогичную приведенной для частного случая n = 2.

Введем векторные обозначения:

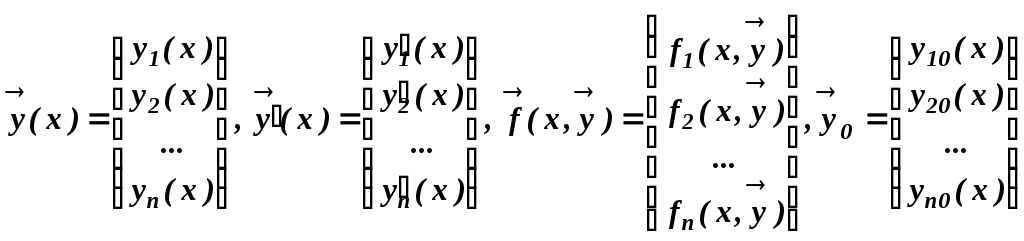
Тогда задача Коши в векторной форме имеет вид:

. (5)

Численное решение задачи Коши (5) состоит в том, что на отрезке [a, b] требуется получить приближенные значения координат вектора в узлах сеткиx_i , i = 1, 2, … , m. Обозначим вектор, аппроксимирующий решение, через , а его координаты – черезy_ki , k = 1, 2, … , n, , i = 1, 2, … , m так, что y_ki = y_k (x_i ) или

Будем искать решение на равномерной сетке с шагом h = (b – a) /m.

Погрешность численного метода оценивается величиной , гдеd_i – погрешность решения на сетке с шагом h в точке x_i :

. (6)

Практически погрешность в точке x_i оценивают по формуле Рунге. Пусть: . – значения численного решения в точкеx_i , полученные для шагов h и h/2 соответственно. Тогда погрешность d_i в точке x_i для вычислений с шагом h/2 выражается приближенным равенством:

, (7)

где р – порядок точности численного метода.

Будем находить решение задачи Коши для системы дифференциальных уравнений с помощью классического метода Рунге-Кутта четвертого порядка. Векторная форма алгоритма метода Рунге-Кутта для задачи (5) имеет вид:

,

,

,

, (8)

,

,

где

Рассмотрим применение этого алгоритма к решению системы двух обыкновенных дифференциальных уравнений (1) с начальными условиями (2):

,

,

,

,

,

,

,

,

.

Задача Коши для дифференциального уравнения n-го порядка ставится следующим образом: найти решение уравнения

(9)

при начальных условиях

(10)

Задача Коши (9)-(10) для дифференциального уравнения n-го порядка приводится к задаче Коши для системы n дифференциальных уравнений первого порядка (3)-(4), к которой применяются методы решения систем.

Обозначим

и выразим функцию y(x) вместе с ее производными до (n-1)-го порядка включительно через введенные функции

.

Вместо задачи (8)-(9) имеем задачу для системы уравнений:

(11)

при начальных условиях

. (12)

Численным решением задачи Коши (8)-(9) является таблица значений функции y₁ в точках x_i , i = 1, … , m.