Варианты
Найти решение
задачи Дирихле для уравнения Пуассона
в прямоугольнике
с шагом разностной сетки по обоим
координатным направлениям0,1:
1. a = 1,2; b = 1,0; f(x1 , x2 ) = 500 x1 x2 ; t1 = 1; t2 = 3; t3 = 10; t4 = 12.
2. a = 1,1; b = 1,0; f(x1 , x2 ) = 500(x1 + x2 ) ; t1 = 1; t2 = 3; t3 = 10; t4 = 12.
3. a
= 1,4; b = 1,0; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
4. a
= 1,5; b = 1,0; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
5. a
= 1,2; b = 1,1; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
6. a
= 1,2; b = 1,2; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
7. a
= 1,2; b = 1,3; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
8. a
= 1,2; b = 1,4; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
9. a
= 1,2; b = 1,5; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
10. a
= 1,1; b = 1,5; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
11. a = 1,2; b = 1,4; f(x1 , x2 ) =4; t1 = 1; t2 = 3; t3 = 10; t4 = 12.
12. a
= 1,3; b = 1,3; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3;
t3 = 10; t4 = 12.
13. a
= 1,4; b = 1,2; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
14. a
= 1,5; b = 1,1; f(x1
,
x2
)
=
;
t1
=
1;
t2 = 3; t3 = 10; t4 = 12.
15. a
= 1,1; b = 1,1; f(x1
,
x2
)
=
;
t1
=
1;
t2 = 3; t3 = 10; t4 = 12.
16. a
= 1,2; b = 1,2; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3;
t3 = 10; t4 = 12.
17. a
= 1,1; b = 1,3; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3;
t3 = 10; t4 = 12.
18. a
= 1,2; b = 1,4; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3;
t3 = 10; t4 = 12.
19. a
= 1,1; b = 1,5; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
20. a
= 1,2; b = 1,0; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
21. a
= 1,4; b = 1,1; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
22. a
= 1,4; b = 1,2; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
23. a
= 1,5; b = 1,3; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
24. a
= 1,5; b = 1,0; f(x1
,
x2
)
=
;
t1
=
1; t2
=
3; t3
=
10; t4
=
12.
Вид рабочего листа ms Excel
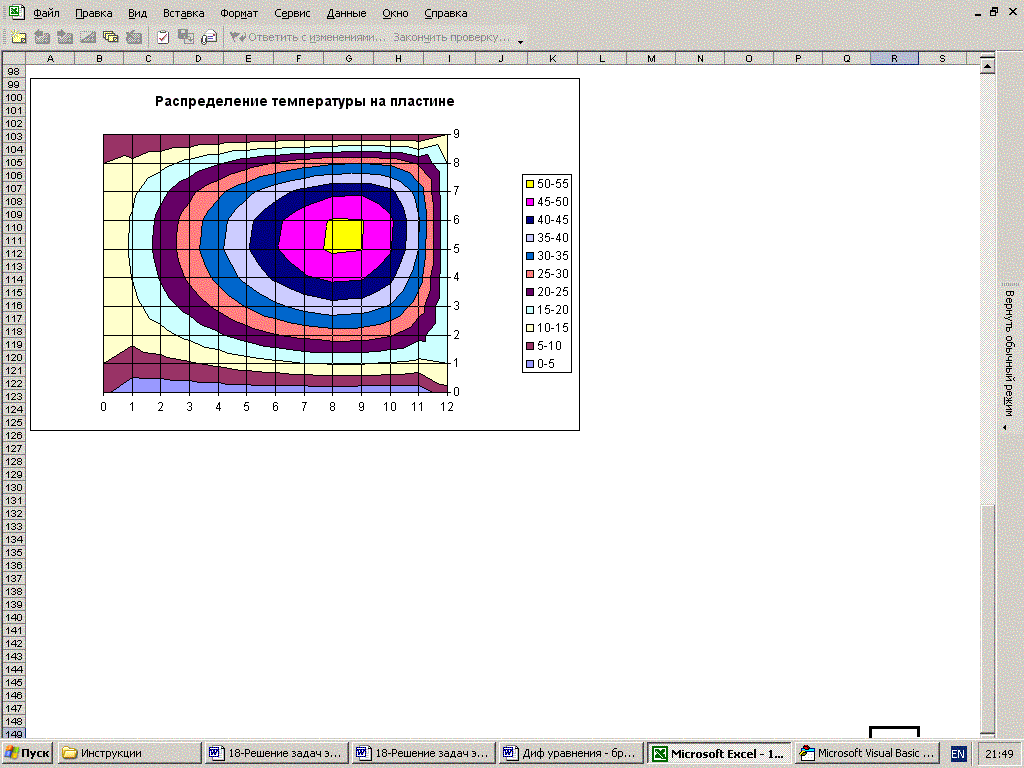
Лабораторная работа № 19 "Решение задач параболического типа" Элементы теории
Типичным примером дифференциального уравнения в частных производных второго порядка параболического типа является уравнение теплопроводности, описывающее процесс распространения тепла в одномерном стержне 0 < x < l:
,
(1)
где u = u(x, t) – температура в точке х стержня в момент t, с – теплоемкость единицы массы, - плотность, с - теплоемкость единицы длины, k - коэффициент теплопроводности, f0 – плотность тепловых источников. Если k, c, постоянны, то (1) можно записать в виде
,
(2)
где
- коэффициент температуропроводности.
Без ограничения общности можно считатьa
= 1, l
= 1.
Действительно, вводя переменные
,
,
,
получим
.
Будем рассматривать
краевую задачу (иногда говорят
начально-краевую задачу) в области
со смешанными краевыми условиями:
(3)
В области
введем сетку
с шагами h
по х
и
по t.
Пусть
- сеточная функция, принимаемая в качестве
приближения искомой функцииu(x,
t).
Аппроксимируем производную по
пространственной переменной разностным
выражением на временном слое
:
.
Можно аппроксимировать
производную по пространственной
переменной разностным выражением на
временном слое
:
.
Рассматриваются
аппроксимации, представляющие собой
линейные комбинации значений при
и
:
.
Производную по t заменим разностным отношением:
.
Обозначим
- некоторую правую часть, например
.
Тогда при
= 0,5
дифференциальное уравнение в задаче
(3) аппроксимируется следующим разностным
выражением:
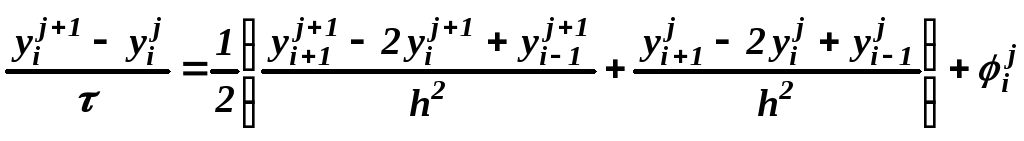(4)
В качестве начальных условий задаем:
.
(5)
Аппроксимацию краевых условий
(6)
выполним также, как в лабораторной работе № 17 "Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка". Тогда после алгебраических преобразований разностная схема для задачи (4)-(6) примет вид:
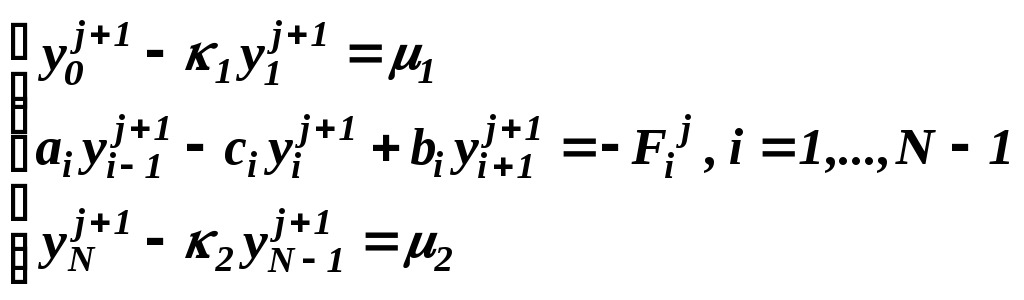(7)
где
(8)
,
(9)
.
(10)
Значения
на новом слое находятся методом прогонки.
вычисления продолжаются до достижения
заданного момента времениТ.
Рассмотренный алгоритм называется
разностной схемой Кранка-Николсона.
Можно показать, что погрешность аппроксимации разностной схемы (7)-(10) имеет второй порядок по обеим переменным O(2 + h2 ).
Схема Кранка-Николсона безусловно устойчива по начальным данным на множестве непрерывных функций для полностью однородной задачи (т.е. f = a1 = b1 = A = B = 0, a0 = b0 = 1) . Но опыт расчетов показывает, что на сеточных начальных и граничных условия, а так же правых частях с большими градиентами эволюционное решение может осcцилировать и даже становится бесконечным. Это означает, что для конкретных задач существует ограничение на шаг по времени при фиксированном шаге пространственной переменной. Данное ограничение выясняется эмпирическим путем в результате тестовых расчетов.
Рассмотрим разные формы граничных условий:
1. Если на границе х=с задана температура Tc , то граничное условие в точке имеет вид: u(c) = Tc .
2. Если на границе х=с задан тепловой поток qc , то граничное условие в точке имеет вид: u(c) = qc .
3. Если на границе х=с задано условие u(c) = 0, то это означает, что данная граница теплоизолирована.
4. Если температура окружающей среды равна T0 , то условие теплообмена с окружающей средой имеет вид: u(c) = (Т - T0 ), где - коэффициент теплопроводности.