
- •Введение
- •1.1 Краткий обзор современных методов проектирования бис.
- •1.2 Маршрут проектирования бис на основе бмк.
- •2.1 Постановка задачи размещения элементов матричных бис. Критерии размещения.
- •2.2 Основные алгоритмы начального размещения элементов бис.
- •2.3 Итерационные алгоритмы оптимизации размещения элементов бис на бмк.
- •3.1 Обоснование выбора алгоритма размещения и оптимизации размещения элементов на бмк.
- •3.2 Описание используемого алгоритма размещения и оптимизации размещения элементов на бмк.
- •5.1 Общие положения.
- •5.4 Расчет дополнительных капитальных вложений.
- •5.5 Данные для расчета.
- •6.1 Особенности работы с компьютером.
- •6.2 Болезни связанные с работой на компьютере.
- •6.3.2 Учет требований охраны труда при организации трудового процесса.
- •6.3.3 Планировка рабочего места.
- •6.3.4 Рабочая поза.
- •6.3.5 Требования к органам управления.
- •6.5 Воздействие излучения.
- •6.6 Основные выводы.
- •7.1 Технологический маршрут изготовления кмоп-ячейки бмк тц-5500.
- •Литература
2.1 Постановка задачи размещения элементов матричных бис. Критерии размещения.
Основная цель, которая ставится в процессе размещения, - создание наилучших условий для последующей трассировки соединений схемы. Она же определяет стратегию выбора формального критерия оптимизации F. Однако из-за условности разделения задач размещения и трассировки построить подобный критерий, достаточно точно отражающий условия прокладки соединений на КП, очень трудно.
Единственным “идеальным” в этом смысле критерием является собственно трассировка соединений, как это, например, происходит при ручном проектировании топологии. К сожалению, громадная вычислительная сложность совместного решения задач размещения и трассировки даже для небольших БИС заставляет применять при их конструировании эвристические критерии качества размещения. Это прежде всего различные приближенные оценки тех интегральных параметров трассировки, изменение которых косвенно характеризует условия ее проведения при заданном размещении элементов на КП.
К таким параметрам относятся:
- суммарная длина соединений БИС;
- суммарная площадь областей реализации ее цепей;
- число трасс, длинна которых больше заданной;
- наибольшая длинна соединительной трассы на КП;
- число пересечений трасс, принадлежащих различным цепям БИС;
- число соединений простейшей конфигурации и т.д..
2.2 Основные алгоритмы начального размещения элементов бис.
К данной группе алгоритмов, называемых конструктивными, относят алгоритмы последовательного размещения по связности, алгоритмы, основанные на методе минимальных сечений (дихотомического деление), и алгоритмы размещения, использующие силовые функции.
Алгоритмы последовательного размещения по связности. Эти алгоритмы являются наиболее изученными алгоритмами начального размещения. Для них характерно строго последовательное назначение элементов на КП, причем выбор очередного элемента основывается на определении “меры связности” каждого из оставшихся элементов с уже размещенными и поиске среди них такого элемента, для которого это значение максимально. Под мерой связности понимают суммарную связность (число общих цепей) элемента с уже размещенными на КП; относительную связность, определяемую отношением суммарной связности элемента и общего числа инцидентных ему цепей. Выбор позиции для элемента проводится согласно критериям оптимальности размещения (обычно это минимум суммарной длины соединений уже размещенных элементов).
Алгоритмы такого типа просты в реализации, обладают низкой вычислительной сложностью, но отличаются сравнительно невысоким качеством получаемого решения. Тем не менее, они часто применяются при проектировании МаБИС, предваряя более эффективные итерационные процедуры оптимизации размещения.
К подобным алгоритмам относится и приведенные ниже методы “роста пучка” и случайного размещения.
Рост “пучка”. Предполагается, что расположение нескольких блоков (“зародышей”) заранее определено. Таковыми блоками или элементами могут быть блоки, реализующие основные функции системы, или контактные площадки для ввода-вывода на кристалле БИС. Далее производится многократная обработка, предусматривающая отбор еще не размещенных блоков, имеющих наиболее сильную связь с уже размещенными, и их размещение таким образом, чтобы гипотетическая длина соединительных проводников была минимальной. Задача окончательного размещения всех блоков может быть решена путем оценки незанятой площади.
Вместе с тем задачу обработки можно упростить, построив модель, в которой длина соединительных проводников между блоками соотнесена с силой притяжения. Так, например, если блоки A, B, C, D (рис. 2.2.1) уже размещены, а блок Е не размещен, то оптимальная область, в которую с учетом указанных соображений он может быть помещен, представляет собой заштрихованный прямоугольник. В терминах динамики группу соединительных проводников можно рассматривать как упругое тело, и задача, таким образом, становится эквивалентной задаче помещения еще неразмещенных блоков в точки, в которых силы притяжения уравновешивают друг друга (точки центров тяжести). Если число блоков равно n, то время, затрачиваемое на решение задачи размещения всех блоков системы, равно O(n2).

Метод случайного размещения. Данный метод предполагает, что итерационным методом может быть получено удовлетворительное решение и позволяет использовать последовательность случайных чисел для определения первоначального варианта компоновки. Метод основан на использовании следующих допущений: а) данные о первоначальной случайной компоновке достаточны в качестве исходных данных для последующей обработки; б) при использовании удовлетворительного приближенного решения, полученного конструктивным методом, во многих случаях останавливаются на локальных оптимальных решениях, которые не удается приблизить к оптимальному решению итерационным методом; в) формирование последовательности случайных чисел дает возможность получить локальное оптимальное решение в окрестности нескольких первоначальных и соответственно возможность выбора наилучшего из них. Основным достоинством этого метода является возможность получения нескольких решений, что невозможно в других методах.
Существует также мнение, отражающее достоинства метода случайного размещения, согласно которому, несмотря на использование любого первоначального размещения, высока вероятность того, что результаты последовательных улучшений будут весьма эффективны.
Алгоритмы дихотомического деления. Целью данных алгоритмов, реализующих иерархический подход к начальному размещению, является создание необходимых условий для более равномерного распределения соединений на кристалле. При этом используется метод последовательного разбиения схемы на все более мелкие группы элементов с одновременным уточнением положения каждой вновь образуемой группы на КП.
На каждом шаге работы алгоритма очередную группу элементов (первоначально всю схему) разбивают на две малосвязные подгруппы А и В. После этого происходит искусственное разграничение возможных мест расположения элементов из групп А и В внутри области КП, первоначально отводившейся исходной группе. Процесс декомпозиции схемы и деления КП продолжается до тех пор, пока все полученные группы не будут состоять из одного элемента.
В общем случае бинарное дерево разбиений схемы может строиться как сверху вниз, так и снизу вверх. При построении дерева снизу вверх вместо процедуры декомпозиции используется аналогичным образом построенная процедура объединения наиболее связанных между собой блоков (групп элементов) нижнего уровня в блоки предыдущего уровня. На последних стадиях процесса в него включаются элементы ввода - вывода, уже назначенные на контактные площадки КП.
К общим недостаткам алгоритмов данного типа нужно отнести их последовательный характер, относительно высокую сложность построения оптимального дерева разбиений схемы, упрощенную оценку потока соединений через сечение. Тем не менее обеспечиваемое ими более равномерное распределение потоков связей на КП предопределило широкое применение подобных алгоритмов в различных САПР топологии МаБИС.
Алгоритмы размещения на основе силовых функций. Данные алгоритмы представляют собой особую группу алгоритмов, основанных на следующей аналогии БИС с механической системой.
Поставим в соответствие множеству элементов БИС систему материальных точек на плоскости, на которые действуют силы притяжения и отталкивания. Пусть силы притяжения прямо пропорциональны расстоянию между элементами, а их наличие определяется принадлежностью элементов одним и тем же цепям схемы. Подобной моделью БИС может служить неориентированный мультиграф G = (E, V), каждое ребро которого моделируется идеальной пружинкой так, что
fij=kijlij, (2.2.1)
где fij - вектор силы притяжения между i-м и j-м элементами; lij - вектор расстояния между i-м и j-м элементами на плоскости; kij - коэффициент жесткости пружинки (вес ребра в графе G).
Тогда за искомое будем принимать такое размещение элементов на непрерывной плоскости, при котором система находится в состоянии статического равновесия (сумма сил, действующих на материальные точки, равна нулю).
Так как силы упругости пружинок прямо пропорциональны величине их растяжения, то матричная форма уравнения сил, действующих на элементы в канонической системе координат, имеет вид
KL = F, (2.2.2)
где K - матрица упругости; L - вектор расстояний до элементов от начала координат; F - вектор внешних сил.
Матрицей упругости К называют симметричную квадратную матрицу порядка n (n - число вершин графа G), каждый элемент которой
Kij =
 (2.2.3)
(2.2.3)
Разобьем все множество элементов Е на два непересекающихся подмножества логических (Ev) и периферийных (Ep) элементов. С учетом этого уравнение (2.2.2) можно переписать в виде
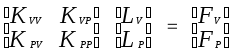 (2.2.4)
(2.2.4)
где Кvv, Kvp, Kpv, Kpp - субматрицы матрицы K; Lv, Lp - векторы расстояний до логических элементов и периферийных элементов ввода - вывода; Fv, Fp - векторы внешних сил, действующих на логические и периферийные элементы.
Одним из обязательных результатов разработки функциональной схемы МаБИС является система тестовой проверки ее работоспособности, в рамках которой каждому вектору воздействий и реакций схемы однозначно соответствует конкретный вход или выход МаБИС. Конструктивно каждый такой вход или выход представляет собой периферийный элемент, который, таким образом, получает привязку к конкретной контактной площадке и, следовательно, заранее определенные координаты на БМК (в случае МаБИС вектор Lp задан). Тогда из условия статического равновесия модельной системы (Fv = 0) и уравнения (2.2.3) следует
![]() (2.2.5)
(2.2.5)
Отсюда легко определить искомые координаты логических элементов: X=Re(Lv), Y=Im(Lv).
Расчет коэффициентов упругости связей между i-м и j-м элементами схемы осуществляется по формуле
![]() (2.2.6)
(2.2.6)
где pijr - вероятность реализации прямой связи (выбора ребра) между i-м и j-м элементами при построении связующего дерева по r-й цепи; nr - число элементов, объединяемых r-й цепью.
Следует отметить, что полученное решение (2.2.6) является единственным и соответствует глобальному минимуму функционала:
![]() (2.2.7)
(2.2.7)
После того, как размещение элементов закончено, их координаты должны быть приведены к позициям КП, так как до этого каждый элемент моделировался материальной точкой и ни его размеры, ни конструктивные ограничения КП не учитывались. Назовем такой процесс дискретизацией полученного решения. Основная цель, которая ставится при ее проведении, - максимально сохранить первоначальное взаимное расположение элементов на плоскости. В качестве формального критерия оптимизации обычно используют минимум суммы сдвигов элементов
![]() (2.2.8)
(2.2.8)
где xi, yi - начальные координаты элемента ei; Xi, Yi - координаты позиции КП, в которую он помещен.
Рассмотрим методы решения этой задачи.
Так как величина сдвига каждого элемента
не зависит от того, на какие именно
позиции КП назначены остальные элементы
схемы, то задача поиска размещения,
отвечающего минимуму D,
может быть сформулирована в виде задачи
линейного назначения или, как ее еще
называют, обычной задачи о назначениях.
Для этого определим матрицу цен назначений
T порядка n, строчки которой
соответствуют элементам схемы, а столбцы
- позициям КП (матрица строится в
предположении, что число элементов и
позиций совпадает, в противном случае
необходимо дополнить схему требуемым
числом фиктивных элементов). Будем
считать, что каждый элемент tij
матрицы T равен расстоянию между
точкой (xi,yi), в которой
размещен элемент ei, и позицией si
на КП. Назовем это расстояние (сдвиг)
ценой назначения ei на si.
Тогда задача оптимального приведения
координат элементов сводится к минимизации
 на множестве всех возможных перестановок
Q={qk} элементов Е на позициях S.
Здесь qk(i) - номер позиции, на которой
размещен ei в перестановке qk.
на множестве всех возможных перестановок
Q={qk} элементов Е на позициях S.
Здесь qk(i) - номер позиции, на которой
размещен ei в перестановке qk.
При небольших n (менее 100) для решения подобных задач целесообразно использовать точные методы, например венгерский алгоритм. Однако на практике число элементов современных БИС значительно превышает это значение. В этих случаях переходят к более простым приближенным методам минимизации D, основанный на упорядочении координат элементов БИС.
Пусть I и J - число горизонтальных рядов и вертикальных столбцов позиций КП. Упорядочим множество элементов Е по возрастанию значений xi и разобьем полученный список на J одинаковых подгрупп по I элементов в каждой. Проведем назначение элементов в позиции КП по следующему правилу: все элементы, попавшие в k-ю подгруппу, размещаются в k-м столбце позиций в порядке возрастания значений yi. Очевидно, что вычислительная сложность метода полностью определяется применяемыми алгоритмами сортировки множества элементов Е.
Для этой же цели может быть использован другой метод дискретизации координат элементов, названный методом приведения по квадрантам. В его рамках приведение координат происходит поэтапно, аналогично тому, как выполняется начальное размещение элементов методом дихотомического деления.
