Раздел 3
Теория погрешностей измерений
Лекция 7
Проверка нормальности распределения
Проверка однородности нескольких серий измерений
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
146 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения
Практически вся теория обработки результатов многократных измерений разработана для нормального распределения случайных величин.
Для возможности применения этой теории необходимо проводить проверку нормальности распределения результатов случайных измерений.
Применение центральной теоремы Чебышева ограничено неопределенностью исходных данных: бесконечное количество бесконечно малых влияющих величин.
Основное допущение: результат измерения подчиняется нормальному закону распределения вероятности.
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
147 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по виду гистограммы
Результаты случайных измерений разбивают на несколько интервалов и строится гистограмма результатов на которую накладывается теоретическая кривая для рассчитанных значений математического ожидания и СКО
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
148 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по виду гистограммы Правила построения гистограммы
1.интервалы на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
2.число интервалов устанавливать в зависимости от числа измерений
(обычно m=√n)
Число измерений |
Рекомендуемое число интервалов |
||
40 . . |
. 100 |
7 . . . |
9 |
100 . . . |
500 |
8 . . . |
12 |
500 . . . |
1000 |
10 . . . |
16 |
1000 . . . |
10000 |
12 . . . |
22 |
3. масштаб гистограммы выбирать так, чтобы ее высота относилась к основанию примерно,как 5 к 8.
4. теоретическая кривая строится по формуле для рассчитанных значений мат. ожидания и СКО
f x |
|
1 |
x mx 2 |
|
|
e 2 2 |
|||
|
2 |
|||
|
|
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
149 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
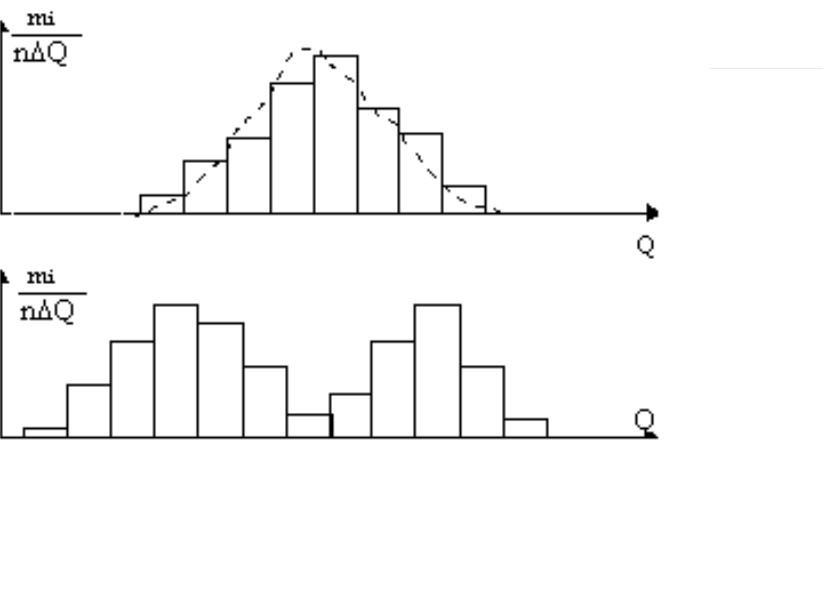
Проверка нормальности распределения по виду гистограммы
гипотеза о нормальности распределения принимается
гипотеза о нормальности распределения отвергается
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
150 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по критерию согласия Пирсена
Критерий согласия Пирсена 2
Мера расхождения: сумма квадратов |
|
|
|
|
|||
отклонения частот mi/n от теоретической |
|
|
|
||||
вероятности Pi попадания отдельного |
|
|
|
|
|||
значения результата измерения в i - й |
|
|
|
|
|||
интервал, причем каждое слагаемое берется с |
|
|
|||||
коэффициентом n /Pi |
|
|
n |
n |
m |
2 |
|
mi – число интервалов |
|
2 |
|||||
|
|
|
|
i |
Pi |
||
n – число измерений |
|
Pi |
n |
||||
Pi - вероятность |
|
|
i 1 |
|
|
||
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
151 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по критерию согласия Пирсена
Критерий согласия Пирсена 2
Если расхождение случайно, то 2 подчиняется распределению К. Пирсона.
Значение 2 сравнивается с табличным значением
02 f (m 3, P)
2 02 гипотеза о нормальном распределении принимается
2 02 гипотеза о нормальном распределении отвергается
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
152 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по критерию согласия Пирсена
Критерий согласия Пирсена 2
Алгоритм обработки многократных измерений:
1. результат измерений определяется как математическое ожидание
M[ X ] mx 1 n xi n i 1
2. определяется СКО
n
xi mx 2
|
i 1 |
|
n 1 |
||
|
3. отбрасываются грубые результаты, погрешности которых превышают 3σ 4. проводят повторные вычисления мат. ожидания и СКО без грубых
результатов
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
153 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по критерию согласия Пирсена
Критерий согласия Пирсена 2
Ошибка первого рода - отклонение верной гипотезы Ошибка второго рода - принятии неправильной гипотезы
Вероятность ошибок зависит от 02 f (m 3, P) и, следовательно вероятности Р
С повышением вероятности для которой принимается2
0
вероятность ошибки первого рода уменьшается, а второго рода увеличивается и наоборот.
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
154 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по критерию согласия Пирсена
Критерий согласия Пирсена 2
Нецелесообразно принимать решение с |
P = 0,9...0,95 |
|
очень высокой степенью вероятности |
||
|
применение критерия К. Пирсона дает хорошие
результаты только, если n>40...50.
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
155 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по составному критерию
Составной критерий
(применяется для малого числа измерений n=10…50)
d-распределение |
проверка выхода |
Алгоритм обработки многократных измерений аналогичен алгоритму используемому в критерии согласия Пирсона
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
156 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по составному критерию
Составной критерий (применяется для малого числа измерений n=10…50)
d-распределение
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
xi mx |
|
|
|
1 |
|
- d-критерий |
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n |
|
|
|
c |
d |
q |
d dq |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
n |
|
|
|
|
2 |
|
||||||
|
|
xi mx |
смещенная |
1 |
1 |
|
1 |
|||||||||
c |
2 |
2 |
||||||||||||||
|
i 1 |
|
|
|
|
|
|
оценка СКО |
||||||||
|
|
n |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d f q1, P, n 1 |
|
|
|
|
|
|||||||||||
q1 |
|
|
|
|
уровень значимости |
|
|
|
|
|||||||
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
157 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по составному критерию
Составной критерий (применяется для малого числа измерений n=10…50)
проверка выхода
критерий q2 определяется по биноминальному распределению
определяем толерантный интервал – это интервал в котором должно находится не менее n – 1 наблюдений
|
m |
zq2 |
1 Cnk 1 p k pn k |
|
k 0 |
|
m=1 для n=10…20 |
|
m=1 для n=20…50 |
zq2 zq2
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
158 |
|
Теория погрешностей измерений Обработка результатов многократных измерений
Проверка нормальности распределения по составному критерию
Составной критерий (применяется для малого числа измерений n=10…50)
Если оба критерия выполняются, то распределение считается нормальным с уровнем значимости q=q1+q2
d |
q1 |
d d |
q1 |
z |
q2 |
z |
|
|
|
||||||
1 2 |
2 |
|
|
q2 |
|||
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
159 |
|