Теория неопределенности измерений Расчет неопределенности измерений
Расчет неопределенности по типу В
Исходными данными для вычисления uВ могут быть:
–данные предшествовавших измерений величин,
входящих в уравнение измерения;
–сведения о виде распределения вероятностей;
–данные, основанные на опыте исследователя или общих
знаниях о поведении и свойствах соответствующих
приборов и материалов;
–неопределенности констант и справочных данных;
–данные поверки, калибровки, сведения изготовителя о приборе и т.п.
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
200 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет неопределенности по типу В
Неопределенности представляют в виде границ отклонения значения величины от ее оценки.
Как правило, постулируется равномерный закон распределения возможных значений величины в указанных границах
Если закон распределения не равномерный, то предлагаемые формулы расчета применять нельзя
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
201 |
|
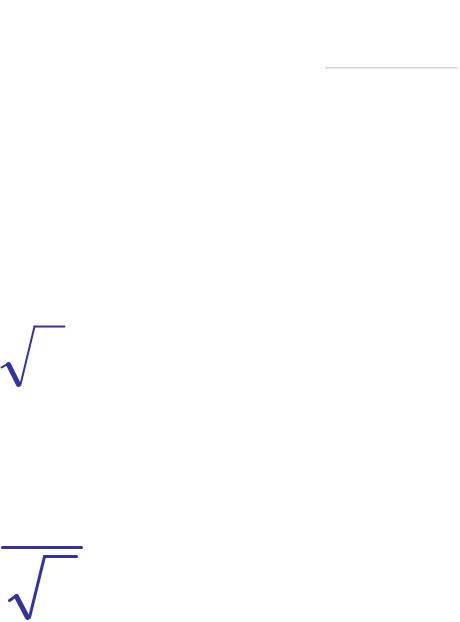
Теория неопределенности измерений Расчет неопределенности измерений
Расчет неопределенности по типу В
bi-, bi+ - нижняя и верхняя границы для i-й входной величины
uB( x |
) |
bi bi |
|
|
|||
i |
2 |
3 |
|
|
|
|
|
если границы симметричные (+bi) uB( xi ) b3i
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
202 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет неопределенности
суммарная стандартная неопределенность (ис): стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерений изменяется при изменении этих величин
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
203 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет коэффициента корреляции
|
|
|
nij |
|
_ |
|
|
_ |
|
|
|
|
r xi , xj |
|
xil xi |
xjl xj |
|
|
|
||||||
|
l 1 |
|
|
|
|
|
|
|
|
|
||
n |
|
|
_ |
2 |
n |
|
_ |
|
2 |
|
||
|
|
|
|
|||||||||
|
|
ij |
|
|
ij |
|
|
|||||
|
|
xil xi |
|
xjl xj |
|
|
||||||
|
|
l 1 |
|
|
|
l 1 |
|
|
|
|
|
|
xil , xjl |
- согласованные пары измерений |
|||||||||||
где l = 1, …, nij;
nij - число согласованных пар результатов измерений
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
204 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет суммарной неопределенности для некореллированных оценок x1 … xm
|
m |
|
f |
|
2 |
|
uc y |
|
|
u2 xi |
|||
x |
||||||
|
|
|
|
|
||
|
i 1 |
|
i |
|
||
y=f(x1…xm) – функция определения выходной величины u(xi) – стандартная неопределенность по типу А или В
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
205 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет суммарной неопределенности для кореллированных оценок x1 … xm
|
m |
|
f |
2 |
m |
m |
f |
|
|
f |
|
r xi , xj u(xi ) u(xj ) |
uc y |
|
|
u2 xi |
|
|
|
||||||
x |
x x |
|
||||||||||
|
|
|
|
|
|
j |
||||||
|
i 1 |
|
i |
i 1 j 1 |
|
i |
||||||
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
206 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет неопределенности
расширенная неопределенность (U):
величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
207 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет расширенной неопределенности
U k uc
k – коэффициент охвата - числовой коэффициент, используемый как множитель при суммарной стандартной неопределенности для получения расширенной неопределенности
При предположении о нормальности закона распределения возможных значений измеряемой величины полагают:
k = 2 при р ≈ 0,95 k = 3 при р ≈ 0,99
При предположении о равномерности закона распределения полагают: k = 1,65 при р ≈ 0,95
k = 1,71 при р ≈ 0,99
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
208 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет коэффициента охвата расширенной неопределенности
k tp veff
tp veff - квантиль распределения Стьюдента с эффективным числом степеней свободы veff и доверительной вероятностью Р
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
209 |
|
Теория неопределенности измерений Расчет неопределенности измерений
Расчет эффективного числа степеней свободы
veff |
|
|
|
|
uc4 |
|
|
|
|
m |
u |
4 |
xi |
|
|
f |
4 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
vi |
|
|
|
|||
|
|
i 1 |
|
|
xi |
||||
vi - число степеней свободы при определении оценки i-й
входной величины
vi = ni - 1 - для вычисления неопределенностей по типу А vi = ∞ - для вычисления неопределенностей по типу В
Электронный образовательный ресурс: «Метрология, стандартизация и сертификация» |
|
доцент, к.т.н. Цыпин А.В. |
210 |
|