
- •1. Введение
- •Крутильный маятник
- •2. Описание установки и метода измерений
- •Измерение жёсткости пружины
- •Измерение момента инерции колебательной системы
- •Теоретический расчёт момента инерции
- •3. Порядок выполнения работы
- •4. Данные установки
- •5. Обработка результатов измерений
- •Измерение жёсткости системы пружин
- •Расчёт момента инерции колебательной системы
- •Контрольные вопросы
3
|
K |
(6) |
ω = |
I . |
Уравнение (5) – дифференциальное уравнение свободных гармонических колебаний.
Его решение
φ(t ) = φ0 cos(ωt + α ) ,
где φ0 и α – константы, определяемые начальными условиями.
Величина ω, определяемая по формуле (6) – циклическая частота гармонических вращательных (крутильных) колебаний. Период этих колебаний
T = |
2π |
= 2π |
I |
. |
(7) |
|
ωK
Таким образом, момент инерции тела пропорционален квадрату периода гармонических вращательных колебаний.
2. Описание установки и метода измерений
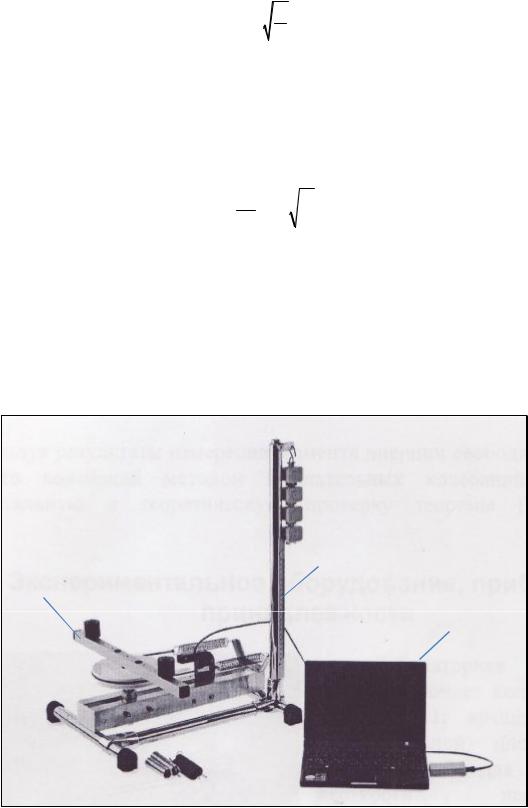
Экспериментальная установка изображена на РИС. 1. Она состоит из двух частей: колебательной системы 1 и устройства 2 для измерения жёсткости пружин. Индикаторным прибором является оптический датчик, подсоединённый к компьютеру 3.
2
1
3
Рис. 1
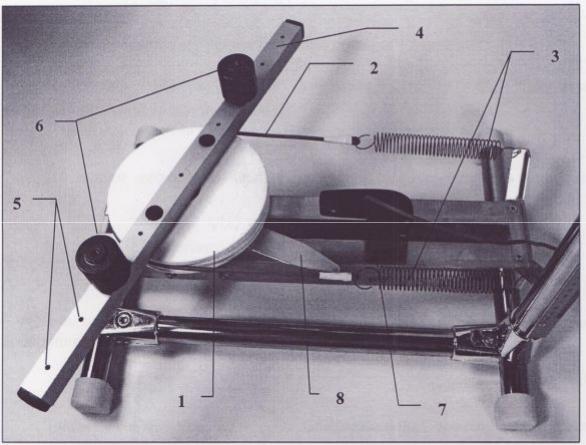
Колебательная система изображена на РИС. 2. Она состоит из закреплённого на вертикальной оси шкива 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки. К шкиву жёстко прикреплён металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6. Вращательные колебания регистрируются оптическим датчиком 7 в форме импульсов при пере-
4
крытии оптической оси датчика язычком 8, жёстко скреплённым со шкивом колебательной системы.
Рис. 2
Эксперимент состоит из двух частей: измерение жёсткости пружины и измерение периода крутильных колебаний системы, состоящей из шкива 1, профиля 4 и грузов 6.
Измерение жёсткости пружины
Для определения вращательного коэффициента жёсткости, входящего в формулу
(4), необходимо измерить жёсткость пружин.
Пусть на пружине подвешен груз массой m0. Запишем II закон Ньютона для этих грузов:
F |
F |
|
0 |
uur |
ur |
упр , |
(8) |
|
т |
+ F |
|||||
|
|
|
|
= F |
|
|
|
uur |
ur |
упр |
– сила упругости. Спроецировав уравнение (8) на вер- |
||||
где т – сила тяжести, |
|
||||||
тикальную ось, получим
Fупр = Fт .
По закону Гука модуль силы натяжения пружины,
Fупр = kl ,
где k0 – жёсткость пружины, l – её удлинение. Модуль силы тяжести
Fт = m0 g ,
где g – ускорение свободного падения. Получим

5
k0l = m0g . |
(9) |
Устройство для измерения жёсткости пружин показано на РИС. 3. Оно состоит из стойки с подвесом, набора калиброванных грузов весом по 100 г каждый и металлической линейки.
Рис. 3
Если на две пружины, соединённые последовательно, как показано на РИС. 3, подвесить грузы суммарной массой m1 и измерить удлинение пружин l1, а затем при грузах массой m2 – удлинение l2, то из (9) получим
|
|
ìk l |
= m g |
|
|
|
||||
|
|
îk0l1 |
= m1 g, |
|
|
|||||
|
|
í |
0 2 |
|
|
2 . |
|
, запишем |
||
|
|
|
|
|
|
|||||
Вычтя верхнее равенство этой системы( ) |
из( нижнего) |
|||||||||
k |
0 |
l - l |
= m -m g |
. |
||||||
Отсюда получим |
2 1 |
|
|
|
2 |
|
1 |
|||
|
k = m |
- m |
g |
. |
(10) |
|||||
|
|
0 |
|
|
2 |
- |
1 |
|
||
|
|
|
l2 |
|
l1 |
|
||||
Результат расчёта по этой формуле не будет зависеть от положения нуля на измерительной линейке.
Величина k0, рассчитанная по формуле (10) – это жёсткость двух пружин, соединённых последовательно. Для одной пружины
|
|
2 |
m |
- m |
. |
(11) |
|||
k = k |
= |
2 |
- |
l1 |
1 |
g |
|||
2 0 |
|
l2 |
|
|
|
||||
6
Измерение момента инерции колебательной системы
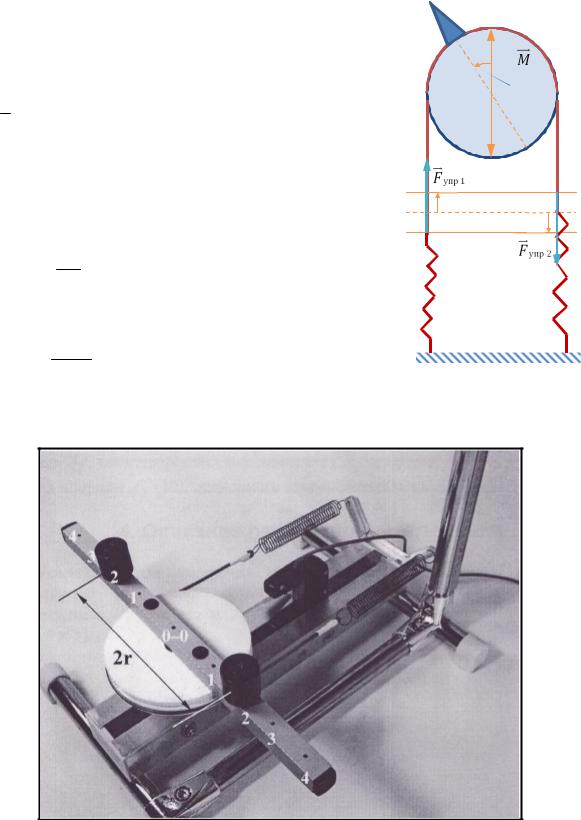
Ремень, связанный с пружинами жёсткостью k (11), надевают на шкив диаметра d и выводят систему из положения равновесия, повернув её на угол φ (РИС. 4). Толстой синей стрелкой на РИС. 4 показано положение язычка. При этом одна пружина оказывается сжатой на
l = d φ , а другая – растянутой на ту же величину. Поэто- 2
му суммарный момент сил упругости станет равным
M |
|
= - F |
d |
= -k |
dφ |
d = - |
kd2 |
φ |
. |
|
|
|
2 |
||||||
|
z |
2 упр 2 |
2 |
|
|
||||
Сравнивая это выражение с равенством (4), видим, что вращательный коэффициент жёсткости
z 8 φ |
d |
l |
l |
K = kd2 |
|
|
|
|
|
|
|||
|
2 |
. |
|
(12) |
|
|
|
|
|
Из формул (7) и (12) получим выражение для момента |
|
|
|||||||
инерции=колебательной системы |
|
|
|
|
|
||||
I |
2 2 |
|
|
|
|
|
|
|
|
|
kd T |
|
|
|
|
|
|
||
|
8π2 |
. |
(13) |
|
|
Рис. 4 |
|
|
|
Момент инерции колебательной системы изменяется |
5 |
||||||||
путём установки, |
снятия и перестановки грузов |
6 |
в различные отверстия |
||||||
|
|
|
|||||||
(РИС. 5).
Рис. 5
Из формулы (13) следует, что моменты инерции подвижной части колебательной системы относятся как квадраты периодов их колебаний. Если I0 – момент инер-
