1.Напряженно-деформированное состояние изотропного тела. Внутренние усилия. Метод сечений. Эпюры внутренних усилий.

Напряженно-деформированное состояние (НДС) - совокупность внутренних напряжений и деформаций, возникающих при действии на неё внешних нагрузок, температурных полей и других факторов.

Центральное растяжение (сжатие) – такой вид деформации, при котором в поперечном сечении возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние силовые факторы равны 0 (система внутренних сил образует равнодействующую, направленную вдоль оси стержня).

Метод сечений – применяют для определения внутренних сил.

Рассмотрим твердое тело.

Рассечем мысленно на 2 части перпендикулярно продольной основной, отбросим часть 2. Действие отброшенной части заменим внутренними усилениями. Из теоретической механики известно, что любую систему сил можно привести к одной точки (основная теорема статики). В результате получим главный вектор и главный момент системы сил . Метод сечений иногда называют методом РОЗУ (рассекем, отбросим, заменим, уравновесим).

Проектируем главный момент и главный вектор на оси декартовой системы.

N_z – продольная сила

Q_x,Q_y – поперечные силы

M_z – момент относительно продольной оси, называется крутящим.

Mx, My- изгибающие моменты.

Для определения внутренних усилий к части тела I можно применить уравнения равновесия:

Эпюра – это график, изображающий изменение внутренних сил по длине конструкции.

Эпюры внутренних усилий.

При построении эпюры растягивающие берутся со знаком «+», сжимающие с «-».

2.Деформация при упругом растяжении и сжатии. Закон Гука. Коэффициент Пуассона.

Гипотеза Бернулли или плоских сечений: проведем сетку на поверхности стержня, эти линии после деформации останутся взаимно перпендикулярными изменится лишь расстояние между ними. Поперечные сечения стержня плоские и перпендикулярны к его оси, до деформации останутся такими же и после деформации существуют только нормальные напряжения.

Продольная сила:

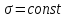, А – площадь поперечного сечения

–относительное удлинение

- абсолютное удлинение

Закон Гука:

- модуль упругости (Юнга)

Для стали марки СТ3

–жесткость сечения

–абсолютное сужение

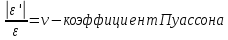
3.Растяжение – сжатие. Напряжения, перемещения. Условия прочности.

Центральное растяжение (сжатие) – такой вид деформации, при котором в поперечном сечении возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние силовые факторы равны 0 (система внутренних сил образует равнодействующую, направленную вдоль оси стержня).

Напряжение – это внутренняя сила, приходящаяся на единицу площади данной точки данного сечения. Измеряется в Па.

[Па]=1[Н/м²]

1МПа=10⁶Па

При растяжении – сжатии касательных напряжений нет

А – площадь данного поперечного сечения

N – продольная сила, кН

Перемещение, м:

Диаграмма напряжения.

Рассмотрим цилиндрический образец захватов разрывной машины.

Изобразим диаграмму растяжений для малоуглеродистой стали

F_b – временное сопротивление, разрыв.

На участке 0-1 выполняется закон Гука, т.е. деформации пропорциональны нагрузкам, начиная с т.2 деформации быстро растут, 2-3 площадка течения, в т.3 конец участка, на котором идет сильная деформация без увеличения нагрузки. В образце т.4 временное сопротивление, разрыв. В т.4 максимальная нагрузка. В т.5 разрушение. Если прервать испытание в т.2 образец возвращается к исходным размерам, т.е. это область упругих деформаций (они исчезают при снятии нагрузки). При продолжении испытания после т.2 образец не возвращается к исходным размерам. Деформации после т.2 пластические или остаточные, они не исчезают после снятия нагрузки.

Предельные допустимые напряжения – это напряжения, при которых возникает опасное состояние (т.е. разрушение или опасная деформация)

Для пластичных материалов:

Для хрупких материалов:

Допустимые напряжения - максимальное напряжение, при котором материал должен нормально работать

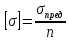
n>1 – коэффициент запаса

Значение зависит от материала, от сложности детали 1,25 12,5