Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
М.В. Девятерикова, П.А. Борисовский
Методы оптимизации
и
исследование операций
Методические указания к выполнению
расчетно-графической работы
Омск 2006
УДК 519.8
ББК 22.18
Д25
Рецензент:
Филимонов Д.В., к.ф.-м.н., ст. преподаватель кафедры “ПиВМ” ОмГУ.
Девятерикова М.В., Борисовский П.А.
Д25 Методы оптимизации и исследование операций: Методические указания к выполнению расчетно-графической работы. – Омск: Изд-во ОмГТУ, 2006. – 24с.
УДК 519.8
ББК 22.18
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
© Девятерикова М.В., Борисовский П.А., 2006
© Омский государственный технический
у
Введение
Задачи поиска наибольших или наименьших значений имеют важное теоретическое и прикладное значение в математике, экономике, информатике и многих других областях. Стремительно возросший в ХХ столетии интерес к методам оптимизации обусловлен прежде всего необходимостью эффективной организации производственной деятельности и рационального использования ресурсов, а также развитием вычислительной техники, позволяющей решать оптимизационные задачи в крупных промышленных масштабах. В более широком понимании оптимизация является средством поиска наилучших управленческих решений и, таким образом, наряду с методами теории вероятностей, имитационного моделирования и т.д. составляет такую область деятельности, как исследование операций. Для наиболее полного представления о современных методах и приложениях исследования операций можно порекомендовать монографию [6].
Линейное программирование, являясь наиболее хорошо изученным разделом оптимизации, успешно применяется при планировании производства, управлении запасами и транспортными потоками, составлении расписаний и т.д. Особую роль в линейном программировании играют задачи с условиями целочисленности переменных. Поиск их решения обычно представляет значительные трудности и требует особых навыков разработки и применения вычислительных алгоритмов.
Полное и глубокое освоение курса «Методы оптимизации и исследование операций» предполагает получение навыков решения практических задач, изучение особенностей применения различных оптимизационных алгоритмов. В данных методических указаниях разработаны варианты типовых заданий по основным темам курса: решение задач линейного программирования графическим методом, прямым и двойственным симплекс-методом, постановка и решение двойственной задачи, решение задачи целочисленного линейного программирования методом отсечения, решение транспортной задачи, составление сетевого графика, решение матричных игр. По каждой теме кратко приведены постановки задач, даны пояснения по формату исходных числовых данных и указания по применению алгоритмов решения. Более подробное описание алгоритмов приведено в [1,2]. В качестве дополнительной литературы можно порекомендовать также [3–5]. При выполнении каждого задания требуется подготовить отчет с описанием всех этапов работы алгоритма. В целях самоконтроля ко всем задачам даны ответы.
Задание 1. Графический метод решения задач линейного программирования
Под задачей
линейного программирования (ЛП) понимается
задача поиска решения
,
которое удовлетворяет системе линейных
равенств или неравенств и на котором
достигается максимальное или минимальное
значение линейной вещественнозначной
функцииf(x).
Общая постановка задачи ЛП:
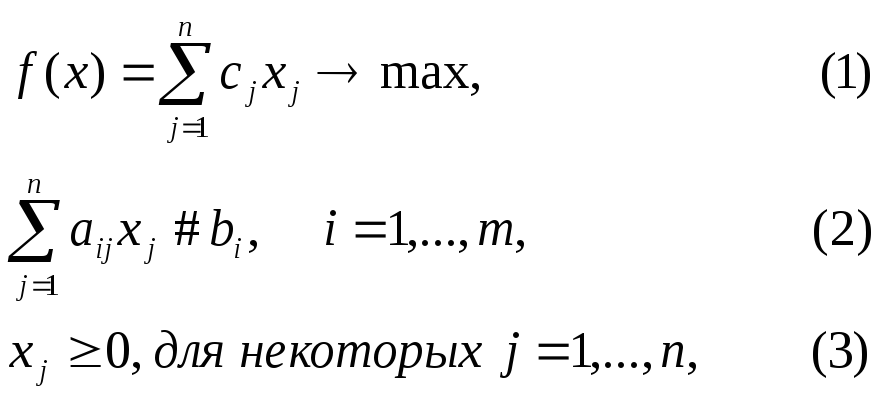
где под знаком “#” понимается любой из знаков “≤”, “≥” и “=”.
Пусть размерность пространства равна 2, т.е. x = (x1,x2). Для каждого ограничения вида ai1x1 + ai2x2 = bi при ai1 ≠ 0 и ai2 ≠ 0 множество допустимых точек представляется в виде прямой на плоскости Ox1x2, проходящей через точки (0, bi / ai2) и (bi / ai1,0). В случае, например, ai1 = 0 получаем горизонтальную прямую x2 =bi / ai2 (разобрать самостоятельно случай bi = 0).
Для ограничений вида ai1x1+ai2x2 ≤ bi и ai1x1+ai2x2 ≥ bi множество допустимых точек является полуплоскостью с границей, определяемой уравнением ai1x1 + ai2x2 = bi. Чтобы выяснить, какая из двух полуплоскостей является допустимой, можно подставить в исходное неравенство некоторую точку, например, точку (0,0). Тогда полуплоскость, содержащая данную точку, будет допустимой или нет в зависимости от того, удовлетворяет ли точка неравенству.
|
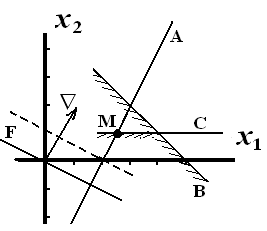
Пример: 2x1 – x2 = 4, соответствует прямой A, x1 + x2 ≤ 5, соответствует полуплоскости под прямой B, x2 ≤ 1, соответствует полуплоскости под прямой C. Допустимая область для всех трех ограничений получается пересечением трех областей и является частью прямой A, лежащей ниже точки M включительно. |
|
Пусть теперь
целевая функция представлена в виде
f(x)=c1x1+c2x2.
Найти оптимальное решение задачи можно
следующим образом: построить прямую,
соответствующую уравнению c1x1+c2x2
= 0, и отметить
вектор градиента
,
который показывает направление роста
функции. Для задач на минимум нужно
отметить вектор антиградиента
.
Далее, путем параллельного сдвига
построенной прямой в отмеченном
направлении, находим самую «крайнюю»
точку пересечения прямой с допустимой
областью. Данная точка и будет решением
задачи.
Пример:
-
Пусть f(x)=x1+2x2, построена прямая F и отмечен вектор градиента. При параллельном сдвиге прямой F вверх крайней точкой её пересечения с допустимой областью будет точка M. Находим её координаты из условия пересечения прямых A и C (решением соответствующей системы из двух линейных уравнений): x1 = 2,5 и x2 = 1. Оптимальное значение равно 4,5.
Варианты заданий:
|
1) 3x1 + 4x2 → max 6x1 + 11x2 ≤ 50 12x1 + 6x2 ≤ 54 6x1 − 3x2 ≥ 15 28x1 + 56x2 ≥ 112 x1, x2 ≥ 0. Ответ: f * = 18,5; x* = (3,5; 2).
|
2) 8x1 + 2x2 → max 22x1 + 7x2 ≤ 77 4x1 + 9x2 ≥ 18 15x1 + 10x2 ≤ 60 4x1 + 8x2 ≤ 16 x1, x2 ≥ 0. Ответ: f * = 4; x* = (0; 2). |
3) x1 + 6x2 → max 14x1 + 21x2 ≤ 28 20x1 + 35x2 ≤ 70 12x1 − 9x2 ≥ 12 21x1 + 15x2 ≤ 75 x1, x2 ≥ 0. Ответ: f * = 4; x* = (4/3; 4/9). |
|
4) 15x1 +13x2 → max 12x1 + 6x2 ≤ 32 8x1 ≤ 9 6x1 +14x2 ≤ 39 4x1 +15x2 ≤ 18 x1, x2 ≥ 0. Ответ: f * = 28,575; x* = (1,125; 0.9).
|
5) 12x1 + 4x2 → max 11x1 + 5x2 ≤ 31 7x1 ≤ 7 2x1 −16x2 ≥ 6 9x1 + 3x2 ≤ 38 x1, x2 ≥ 0. Ответ: f * = 14; x* = (1; 0,5). |
6) 2x1 + x2 → max 14x1 + 10x2 ≤ 23 2x1 + 8x2 ≤ 25 15x1 + 6x2 ≤ 32 18x1 − 5x2 ≤ 26 x1, x2 ≥ 0. Ответ: f * = 3,2; x* = (1,5; 0,2). |
|
7) 7x1 + 6x2 → max 20x1 + 6x2 ≤ 15 16x1 − 2x2 ≤ 18 8x1 + 4x2 ≤ 20 13x1 + 3x2 ≤ 4 x1, x2 ≥ 0. Ответ: f * = 8; x* = (0; 4/3). |
8) 7x1 + 5x2 → max 4x1 + 4x2 ≤ 26 3x1 − 16x2 ≥ −18 14x1 − 2x2 ≤ 10 18x1 + 16x2 ≤ 8 x1, x2 ≥ 0. Ответ: f * = 28/9; x* = (4/9; 0). |
9) 4x1 + x2 → max x1 + 5x2 ≤ 6 16x1 + 4x2 ≤ 12 10x1 + x2 ≤ 6 3x1 − 3x2 ≤ 43 x1, x2 ≥ 0. Ответ: f * = 3; x* = (0,5; 1). |
|
10) x1 + 3x2 → max −3x1 + 16x2 ≤ 32 5x1 + 6x2 ≤ 17 14x1 + 5x2 ≤ 30 4x1 + 4x2 ≤ 5 x1, x2 ≥ 0. Ответ: f * = 3,75; x* = (0; 1,25).
|
11) −2x1 → max 5x1 + 5x2 ≤ 39 −2x1 + 14x2 ≤ 5 2x1 − 12x2 ≥ 6 −x1 + 10x2 ≤ 6 x1, x2 ≥ 0. Ответ: f * = −6; x* = (3; 0). |
12) 2x1 + 3x2 → max 8x1 + 9x2 ≤ 36 10x1 +14x2 ≥ 12 4x1 + 8x2 ≤ 16 6x1 − 3x2 ≤ 9 x1, x2 ≥ 0. Ответ: f * = 7; x* = (2; 1). |
|
13) 4x1 + 7x2 → max 5x1 + 15x2 ≤ 16 2x1 + 3x2 ≥ −1 − x1 + 14x2 ≤ 7 − x1 + 4x2 ≥ 1 x1, x2 ≥ 0. Ответ: f * = 9,8; x* = (1,4; 0,6).
|
14) 9x1 + 2x2 → max 11x1 +2x2 ≤ 42 −2x1 + 8x2 ≤ 19 14x1 + 6x2 ≤ 38 13x1 + 2x2 ≤ 26 x1, x2 ≥ 0. Ответ: f * = 19,6; x* = (1,6; 2,6). |
15) 5x1 + 6x2 → max 13x1 + 5x2 ≤ 18 3x1 + x2 ≤ 4 4x1 + 8x2 ≤ 10 2x1 +11x2 ≥ 6 x1, x2 ≥ 0. Ответ: f * = 9,7; x* = (1,1; 0,7). |
|
16) 3x1 + 5x2 → max 15x1 + 10x2 ≤ 60 2x1 − 3x2 ≥ 1 28x1 + 56x2 ≥ 112 10x1 + 15x2 ≤ 45 x1, x2 ≥ 0. Ответ: f * = 85/6; x* = (2,5; 4/3).
|
17) 2x1 + 11x2 → max 16x1 + x2 ≤ 19 13x1 + 20x2 ≤ 14 10x1 + 6x2 ≤ 13 6x1 − 3x2 ≤ 6 x1, x2 ≥ 0. Ответ: f * = 7,7; x* = (0; 0,7). |
18) 4x1 + 5x2 → max 9x1 ≤ 15 15x2 ≤ 6 −2x1 + 13x2 ≤ 31 2x1 + 3x2 ≤ 39 x1, x2 ≥ 0. Ответ: f * = 26/3; x* = (5/3; 2/5).
|
|
19) 13x1 + 8x2 → max 9x1 + 3x2 ≤ 28 9x1 + 8x2 ≤ 35 x1 + 8x2 ≤ 40 2x1 + 7x2 ≤ 20 x1, x2 ≥ 0. Ответ: f * = 136/3; x* = (8/3; 4/3). |
20) 5x1 + 9x2 → max 8x1 − 5x2 ≤ −3 −3x1 + 12x2 ≤ 42 2x1 + x2 ≤ 44 5x2 ≤ 11 x1, x2 ≥ 0. Ответ: f * = 24,8; x* = (1; 2,2). |
|