1. Множества

1.1. Основные понятия теории множеств

Одними из основных, исходных, понятий математики являются понятия множества и его элементов. Под множеством мы понимаем совокупность определенных, отличных друг от друга, но однотипных объектов, называемых элементами множеств, подчиняющихся счету. Таким образом, множество состоит из элементов. Принято обозначать множества прописными буквами латинского алфавита (A,B,C,…,Z), а элементы множеств – строчными буквами (a,b,c,...,z), цифрами, а также идентификационными выражениями. Примерами множеств могут служить: множество натуральных чисел, множество студентов в группе, множество групп на факультете и т.д.

Принадлежность элемента а множеству М обозначается знаком  (а М); непринадлежность элемента а множеству М обозначается знаком  (а М).

Множество А называется подмножеством множества В (A  B), если всякий элемент А является элементом В. При этом говорят, что В содержит или покрывает множество А. Множества А и В равны (A = B), если их элементы совпадают, иначе: A  B и В  А. Выражение (A ≠ B) является отрицанием предыдущего. Если A  B и В  А, то А часто называют собственным, строгим или истинным подмножеством В (A  B), знак  называется знаком строгого включения.

Множества могут быть конечными, т.е. множества с конечным числом элементов, и бесконечными. Учитывая прикладное значение курса и его использование для изучения основ синтеза конечных автоматов, мы будем рассматривать конечные множества. Число элементов в конечном множестве М называется мощностью и обозначается |М|. Если множество не содержит элементов, то оно называется пустым и обозначается . Принято считать, что пустое множество является подмножеством любого множества.

Множество может быть задано перечислением (списком элементов), порождающей процедурой или описанием характеристических свойств, которыми должны обладать его элементы. Списком можно задавать лишь конечные множества. Список заключается в фигурные скобки. Например, А = {a, b, d, h} означает, что множество А состоит из четырех элементов a, b, d и h.

Порождающая процедура описывает способ получения элементов множества из уже полученных объектов. Примером может служить М – множество всех чисел вида π/2 ± kπ, где k  N (N – множество натуральных чисел).

Задание множества описанием его свойств, пожалуй, наиболее обычно. Например, множество всех четных чисел от 0 до 100. Когда свойство элементов может быть описано коротко выражением Р(х), что означает – элемент х обладает свойством Р , то множество задается выражением М = {х | Р(х)}, которое читается так: М – это множество х, обладающих свойством Р. Например, М = {х | х =π/2 ±kπ, где k  N }. К описанию свойств следует предъявлять требование точности и недвусмысленности.

1.2. Операции над множествами

Множества можно определять при помощи операций над некоторыми другими множествами и подмножествами. Пусть дана некоторая совокупность предметов, которую можно обозначить как множество

V ={ a, b, c, d, e, f, g, h, i, j, k }.

Предположим, что часть предметов, а именно: a, b, d и f имеют круглую форму, а часть – b, c, d, h, и i – окрашена в белый цвет. В этом случае говорят, что множество V имеет два подмножества А = { a, b, d, f } и В = { b, c, d, h, i } круглых и белых предметов. Можно говорить иначе: исходное множество называется фундаментальным или универсумом, а подмножества А и В – просто множествами.

В результате получим четыре класса элементов:

С₀ ={ e, g, j, k } – элементы, которые не обладают ни одним из названных свойств,

С₁ ={ a, f } – элементы, обладающие только свойством А (круглые),

С₂ ={ c, h, i } – элементы, обладающие только свойством В (белые),

С₃ ={ b, d } – элементы, обладающие одновременно двумя свойствами.

Операции над множествами удобно изображать с помощью графической диаграммы Эйлера-Венна (рис. 1).

Рис. 1 . Диаграмма Эйлера-Венна для двух множеств А и В

Объединением множеств А = { a, b, d, f } и В = { b, c, d, h, i } назовем множество А  В = { a, b, c, d, f, h, i }. Таким образом, объединением охватываются три класса элементов – С₁, С₂, С₃, которые на диаграмме заштрихованы (рис. 2). При этом оба множества могут и не пересекаться, т.е. не иметь общих элементов. Логическую операцию объединения двух множеств можно охарактеризовать словами: элемент принадлежит множеству А или множеству В. То, что элемент х принадлежит А или В, можно выразить формулой

х  А  В = (х  А)  (х  В),

где  – символ логической связки или, которая называется дизъюнкцией.

Пересечением множеств А и В называется множество K = А В, содержащее те элементы из А и В, которые входят одновременно в оба множества. Для нашего примера будем иметь (рис. 3):

K =А В = {a, b, d, f}  {b, c, d, h, i} = {b, d} = С₃.

То, что элемент х принадлежит одновременно двум множествам А и В, можно выразить формулой

х  А  В = (х  А) (х  В),

где  – символ логической связки и, которая называется конъюнкцией.

Рис. 2. А  В Рис. 3. А  В

Рассмотрим области С₁ и С₃, образующие множество А (рис. 4). Тогда области С₂ и С₀ образуют множество элементов, не входящих в А (рис. 5). Это обозначается как . Объединение или дизъюнкция множеств А и даст весь универсум V (А  =V), а пересечение или конъюнкция даст нам нулевое множество ; ( А = ). Таким образом множество дополняет множество А до универсума V, отсюда название – дополнительное множество или дополнение как операция. Операцию дополнения иначе еще называют инверсией.

Рис. 4. А Рис. 5.

После рассмотрения операции инверсии (дополнения) все четыре области С_j на диаграмме можно выразить следующим образом:

С₀ =  , С₁ = А  , С₂ =  В, С₃ = А  В.

Используя инверсию, можно представить любую множественную операцию, например объединение:

А  В = (А  ) ( В) (А  В).

Операции дополнения или инверсии объединения и пересечения множеств называются соответственно стрелкой Пирса (D =) и штрихом Шеффера (K =), которые обозначаются соответственно А↓В и А/В. Диаграммы для этих операций представлены на рис. 6 и 7.

Рис. 6. А↓В Рис. 7. А/В

Рис. 8. ( В ← А ) Рис. 9. (В → А)

Разностью между множествами В и А называется совокупность тех элементов множества В, которые не вошли в множество А (рис. 8). Такая операция называется еще запретом А и обозначается ( В ← А ). Для нашего случая это будет область С₂.

При этом ( В ← А ) =  В.

Рис. 10. (А  В) Рис. 11. (А  В)

Дополнением к запрету служит импликация А. На диаграмме Эйлера-Венна это частичное включение множества В в множество А (рис. 9). Обозначается такая операция (В → А). При этом (В → А) = А  .

а b c

Рис. 12. (А  В)  (А  С)

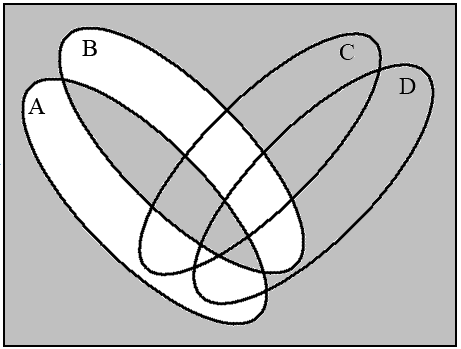
a (А  B) b ((А  B)→(C  D))

c ((А  B)/(C  D)) d ((А  B)→(C  D)) 

 ((А  B)/(C  D))

Рис.13. Диаграммы Венна для операций над четырьмя множествами

Аналогично определяются запрет В (А ← В) = А  и импликация В (А → В) =  В.

Остается привести еще две взаимно дополняющие операции – симметрическую разность или неравнозначность и эквивалентность или равнозначность.

Равнозначность определяется теми элементами множеств А и В, которые для них являются общими, а также элементами, не входящими ни в А, ни в В. В нашем случае это будут области С₀ и С₃ (рис. 10). Обозначается равнозначность А  В или А ~ В.

А ~ В = ( ) (А  В).

Неравнозначность есть объединение двух разностей или двух запретов. Эта операция обозначается (А  В). Таким образом,

(А  В) = (А ← В)  ( В ← А ), или (А  В) = ( В)  (А  ).

На диаграмме Эйлера-Венна это области С₁ и С₂ (рис. 11). Неравнозначность имеет еще название строгая дизъюнкция. Эту операцию можно передать словами: «либо А, либо В».

Диаграммы Эйлера-Венна достаточно наглядно иллюстрируют операции над тремя и четырьмя множествами. Рассмотрим операцию (А  В)  (А  С) и построим диаграммы Эйлера-Венна для трех множеств. Диаграмма на рис. 12а изображает операцию (А  В), а на рис. 12b – (А  С). Конъюнкцию этих соотношений иллюстрирует результирующая диаграмма на рис. 12с.

Для четырех множеств четыре круга Эйлера не дают полную диаграмму Венна, поскольку их пересечение дает только 14 областей, а необходимо 16. Поэтому круги необходимо деформировать в эллипсы. Покажем на примере построение диаграммы для выражения ((А  B)→(C  D))  ((А  B)/(C  D)).

На рис. 13 изображены четыре диаграммы, соответствующие указанной последовательности операций. Последняя диаграмма (рис. 13d) является результирующей.