
Модуль 2 Векторная алгебра
.pdf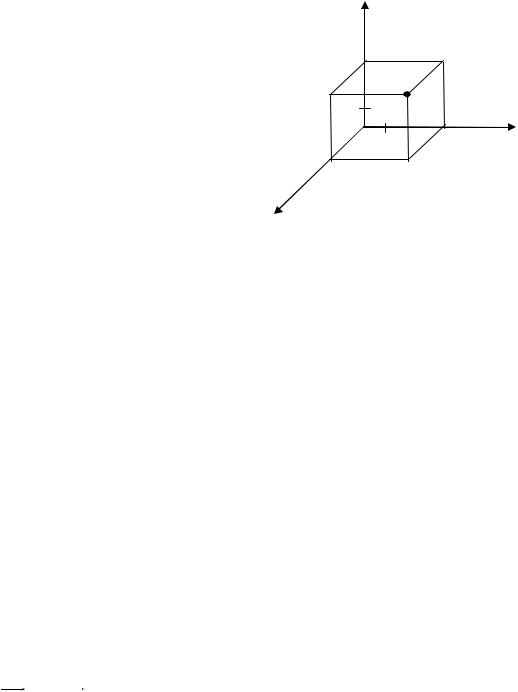
Глава 8. Векторная алгебра.
8.1. Декартова прямоугольная система координат в
пространстве.
Декартова прямоугольная система координат (ДПСК) в пространстве
задается тремья взаимно перпендикулярными плоскости Оху, Oyz, Oxz делят пространство на
8 частей (октанты). Пусть в пространстве задана декартова прямоугольная система координат Охyz, М – произвольная точка в пространстве. Проведем через нее три плоскости, перпендикулярные осям Ох, Oy, Oz.
Точки их пересечения с осями Ох, Oy, Oz
обозначим через M x , M y , M z (Рис. 8.1).
осями Ох, Oy, Oz. Координатные
z
Mz
|
|
M(x,y,z) |
|
|
O |
|
Mx |
My y |
|
|
|
x |
|
Рис. 8.1. |
|
|
Определение 8.1. Прямоугольными координатами точки M называются
величины |
отрезков |
x OM x , |
y OM y , |
z OM z . Координата |
x называется |
|
абсциссой, |
y - ординатой, z – аппликатой точки М. Обозначение: M (x, y, z) . |
|
||||
Таким |
образом, |
при выбранной системе координат каждой точке |
M |
|||
пространства Oxyz |
соответствует единственная тройка чисел |
(x, y, z) - |
ее |
|||
прямоугольные координаты, и обратно: каждой тройке чисел (x, y, z) соответствует единственная точка M в пространстве Oxyz.
8.2. Векторы.
Определение 8.2. Любая упорядоченная пара точек А и В пространства определяет так называемый направленный отрезок. Если А – первая точка, ее называют началом направленного отрезка, В – его концом. Направление от начала к концу считается направлением направленного отрезка. Направленный отрезок называется вектором.
Обозначение: AB (или a ).
127

Определение 8.3. Вектор, у которого начало и конец совпадают, называется
нулевым. Обозначение: 0 .
Определение 8.4. Расстояние между началом и концом вектора называется
длиной вектора. Обозначение: AB или a .
Определение 8.5. Вектор, длина которого равна единице, называется
единичным вектором. Обозначение: e .
Определение 8.6. Векторы a и b называются коллинеарными, если они лежат
на одной прямой или на параллельных прямых. Обозначение: a || b .
Коллинеарные векторы a и b могут быть направлены одинаково ( a b ) и
противоположно ( a b ). Нулевой вектор считаем коллинеарным любому вектору.
Определение 8.7. Единичный вектор, направление которого совпадает с направлением оси l, называется ортом оси l.
Определение 8.8. Векторы a и b называются равными ( a = b ), если 1) они коллинеарны ( a || b ), 2) одинаково направлены ( a b ), 3) имеют одинаковые
длины, т.е. a = b .
Из этого определения следует, что вектор можно перемещать в пространстве параллельно самому себе. Такие векторы называются свободными.
Определение 8.9. Векторы a , b , c в пространстве называются
компланарными, если они лежат в одной плоскости или на параллельных
плоскостях.
8.3. Линейные операции над векторами, их свойства.
Линейными операциями являются операции сложения векторов и умножения вектора на число.
8.3.1. Сложение векторов.
Определение 8.10. Пусть a и b - произвольные векторы. От конца вектора a
отложим вектор b . Вектор a b , соединяющий начало вектора a с концом вектора
128
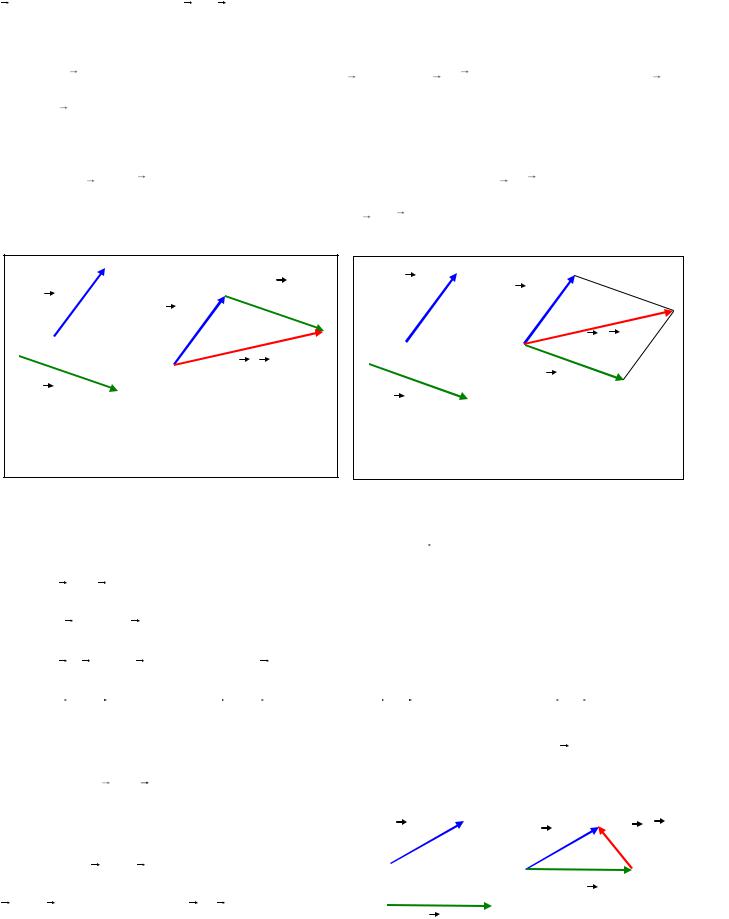
b , называется суммой a и b .
Это правило сложения векторов называется правилом треугольника: начало вектора b совмещается с концом вектора a ; вектор a b направлен от начала a к
концу b (Рис. 8.2).
Сумму двух векторов можно построить по правилу параллелограмма: начала векторов a и b совмещаются в одной точке; вектор a b есть диагональ параллелограмма, построенного на векторах a и b (Рис. 8.3).
|
b |
|
a |
|
a |
|
|
a |
|
|
|
|
|
||
|
|
|
|
|
|
||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a+b |
|
a+b |
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.2. |
|
|
|
Рис. 8.3. |
|
||
8.3.2. Умножение вектора на число. |
|
|
|
|
|
|
|
Определение |
8.11. Произведением |
вектора |
a |
на |
число |
R |
называется |
вектор b a , удовлетворяющий условиям:
1)| b | | | | a |,
2)b || a , т.е. b коллинеарен a ,
3)b a , если 0 ; b a , если 0; b 0 , если 0 или a 0 .
Определение 8.12. Вектором, противоположным вектору a , называется вектор 1 a a .
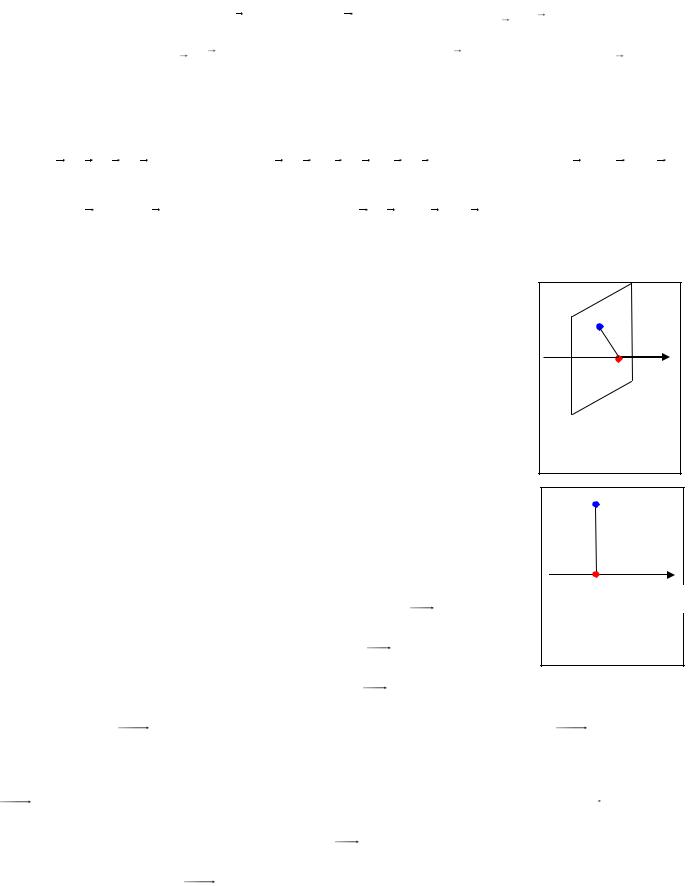
Определение 8.13. Разностью
векторов a и b называется вектор
a |
a |
a - b |
a ( b) . Обозначение: a b (Рис. 8.4).
129
b
b
Рис. 8.4.
|
При вычитании вектора b из вектора a начала векторов a и b |
совмещаются в |
||||||||||||
одной точке и вектор a b направлен от конца вектора b к концу вектора |
a . |
|||||||||||||
|
Предложение 8.1. Линейные операции над векторами обладают следующими |
|||||||||||||
свойствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. a b b a . |
|
2. a b c a b c . |
|
3. a a a . |
|||||||||
|
4. a a , , R . |
|
|
5. a b a a . |
|
|
|
|
||||||
|
8.4. Проекция вектора на ось, основные свойства. |
|
|
|
||||||||||
|
8.4.1. Проекция вектора на ось. |
|
|
|
|
|
|
|
|
|
||||
|
Пусть в пространстве заданы точка М и ось l (направленная |
М |
|
|
||||||||||
|
|
|
|
|||||||||||
прямая). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 8.14. Проекцией точки М на ось l называется |
М1 |
l |
|||||||||||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
основание М1 перпендикуляра, опущенного из точки М на ось l . |
|
|
|
|||||||||||
|
Точка М1 есть точка |
пересечения оси |
l с |
плоскостью, |
Рис. 8.5. |
|||||||||
проходящей через точку М перпендикулярно оси l (Рис. 8.5). |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
Если точка М и ось l заданы на плоскости, точка М1 |
есть |
|
|
|
|||||||||
точка пересечения оси l |
с прямой, |
проходящей через точку М |
|
|
|
|||||||||
перпендикулярно оси l (Рис. 8.6). |
|
|
|
|
|
|
М1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
Пусть в пространстве заданы ось l и вектор AB и |
A1 , |
B1 - |
|
|
|
||||||||
проекции на ось l начала A и конца В вектора AB соответственно. |
Рис. 8.6. |
|||||||||||||
|
|
|
||||||||||||
|
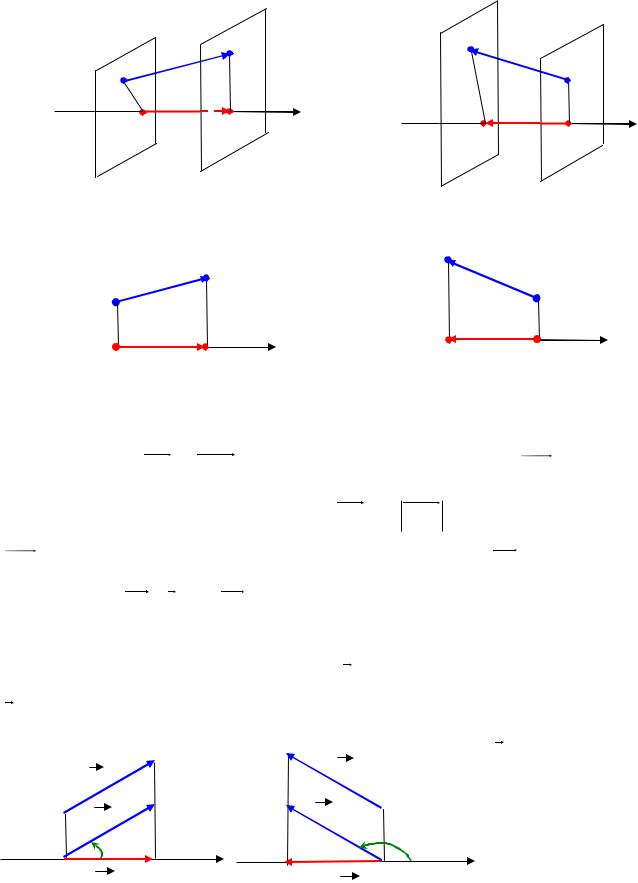
Определение 8.15. Проекцией вектора AB на ось l |
называется число, |
равное |
|||||||||||
длине вектора A1B1 |
, взятое со знаком «+», если направление вектора A1B1 совпадает |
|||||||||||||
с |
направлением |
оси |
l, |
и |
со |
знаком |
«–», |
если |
направление |
вектора |
||||
A1B1 противоположно направлению оси l (Рис.8.7,8.8). Обозначение: прl AB . |
|
|
||||||||||||
|
В частности, если ось |
l, |
вектор |
AB заданы |
на |
плоскости, |
случаи, |
когда |
||||||
направление вектора A1B1 |
совпадает |
с направлением |
оси |
l и противоположно |
||||||||||
направлению оси l показаны на Рис. 8.9 и Рис. 8.10 соответственно. |
|
|
|
|||||||||||
130
|
B |
|
|
|
|
|
|
|
B |
|
|
A |
|
|
|
|
|
|
|
|
|
|
A |
A1 |
B1 |
l |
B1 |
A1 |
l |
|
|||||
|
|
|
|
|
|
Рис. 8.7. |
|
|
Рис. 8.8. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
B |
|
|
|
|
A |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
l |
|
|
|
|
|
l |
|
B1 |
||
|
A1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
B1 |
|
|
|
|
||
|
|
|
Рис. 8.9. |
|
|
Рис. 8.10. |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Итак, |
прl AB |
A1B1 |
, если |
направление вектора A1B1 |
совпадает с |
||||
|
|
|
|
|
|
|
|
|
|
направлением оси l (Рис.8.6, 8.9), прl AB A1B1 , если направление вектора
A1B1 противоположно направлению оси l (Рис.8.7, 8.10); прl AB = 0, если точки A1 ,
B1 совпадают ( AB 0 или AB l ).
8.4.2. Основные свойства проекции вектора на ось.
Пусть в пространстве заданы вектор a и ось l. Пусть φ – угол между вектором a и осью l. Очевидно, что 0 . На Рис. 8.11, 8.12 показан случай, когда вектор
|
a |
|
|
a |
и ось l |
заданы |
на |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
плоскости: |
и |
|||
a |
a |
|
|
2 |
||||
|
φ |
|
|
|
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
l |
|
|
l |
2 |
|
|
|
|
a1 |
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.11. |
131 |
|
|
|
|
|
|
|
|
Рис. 8.12. |
|
|
|
|
|
|
|

Теорема 8.1. Проекция вектора a на ось l равна произведению модуля вектора a на косинус угла φ между вектором a и осью l, т.е. прl a a cos .
Доказательство. Рассмотрим три случая: 1) 0 2 . Тогда прl a a1 a cos .
2) 2 . Тогда прl a a1 a cos a cos .
3) 2 . Тогда прl a 0 a cos .
Следствие 8.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол –
прямой.
Следствие 8.2. Проекции равных векторов на одну и ту же ось равны.
Предложение 8.2. Пусть заданы векторы a , b и ось l. Линейные операции над
проекциями вектора на ось обладают следующими свойствами:
1). прl a b прl a прl b , |
2). прl a прl a , где R . |
Следствие 8.3. Проекция линейной комбинации векторов a , b на ось l равна |
|
линейной комбинации проекций векторов a , |
b на ось l: |
прl a b прl a прl b , |
, R . |
8.5. Базис и координаты вектора. Ориентация базиса.
8.5.1. Базис и координаты вектора на прямой.
Пусть даны прямая l и ненулевой вектор a , лежащий на ней (Рис. 8.13). По лемме о коллинеарных векторах любой вектор b , также лежащий на прямой l,
может быть представлен в виде b a , R и
такое представление единственно. Это означает, что
l
любой вектор на прямой l, с использованием операции умножения вектора на число может быть
однозначно выражен через вектор a .
132

Определение 8.16. Базисом на прямой l называется любой ненулевой вектор a ,
лежащий на этой прямой.
Пусть b a , тогда число R будем называть координатой вектора b в
базисе a и обозначать b ( ) .
Таким образом, базисом на прямой является любой ненулевой вектор. Отметим,
что геометрическая размерность прямой равняется единице.
8.5.2. Базис и координаты вектора на плоскости и в пространстве.
Рассмотрим более общий случай плоскости или пространства и попытаемся ответить на следующий вопрос: сколько и каких векторов нужно задать, чтобы через них с помощью операции сложения векторов и умножения вектора на число можно было бы однозначно выразить любой другой вектор? Ответ на этот вопрос дают следующие две теоремы, доказательство которых можно найти в стандартных школьных учебниках.
Теорема 8.2. Любой вектор, лежащий на плоскости π, можно разложить по двум данным неколлинеарным векторам, лежащим в этой же плоскости, притом единственным образом.
Теорема 8.3. Любой вектор в пространстве можно разложить по трем некомпланарным векторам и притом единственным образом.
Определение 8.17. Базисом на плоскости называется любая упорядоченная
пара неколлинеарных векторов.
Определение 8.18. Базисом в пространстве называется любая упорядоченная
тройка некомпланарных векторов. |
|
Что означает упорядоченная? |
|
Рассмотрим некоторую плоскость π и три вектора a , b , c . Пусть a , b - |
|
неколлинеарны. Тогда по теореме 8.2. можно записать: |
|
c a b , |
(8.1) |
где , R . |
|
133

Будем считать a - первым, b - вторым. Тогда запись , в базисе a , b
однозначно определяет вектор c .
Определение 8.19. Числа , называются координатами вектора c в базисе a , b . Обозначение: c , .
А если будем считать вектор b - первым, a - вторым, тот же самый вектор c
можно записать в виде c = , .
Легко видеть, что запись вектора c через и , которые называются
координатами вектора c в заданном базисе, зависит от того, какой вектор считать первым, а какой вторым. Таким образом, для заданной пары неколлинеарных
векторов a и b существует 2 базиса: a , b и b , a на плоскости.
Впространстве принципиально ничего не меняется, только вместо (8.1) имеем
всоответствии с теоремой 8.3. следующее разложение:
d a b c , |
(8.2) |
где a , b , c - некомпланарные векторы, , , R . |
|
Определение 8.20. Числа , , называются |
координатами вектора d в |
базисе a , b , c . Обозначение: d , , .
Замечание. Плоскость является геометрическим пространством размерности 2 и
базис состоит из 2 векторов. Пространство имеет размерность 3 и базис состоит из 3
векторов.
Упражнение. Сколько базисов существует для трех заданных некомпланарных векторов в пространстве?
Определение 8.21. Базис называется ортогональным, если все базисные векторы попарно перпендикулярны.
Замечание. Будем считать, что нулевой вектор ортогонален любому вектору.
Определение 8.22. Ортогональный базис, у которого длины всех базисных векторов равны единице, называется ортонормированным.
134

|
|
|
Пример 8.1. На плоскости базис i, j |
такой, что |
i j , |
|
i |
1, |
|
j |
1 образует |
|||||||||
ортонормированный базис. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример |
|
8.2. В пространстве базис |
i, j, k такой, |
что |
i j , |
|
i k , |
j k , |
|||||||||
|
i |
|
1, |
|
j |
|
1, |
|
k |
|
1 образует ортонормированный базис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.5.3. Ориентация базиса.
Введем понятие ориентации тройки некомпланарных векторов. Пусть даны два ортонормированных базиса e1 ,e2 ,e3 и f1 , f2 , f3 . Можно ли совместить эти базисы при помощи перемещения в пространстве?
Понятно, что векторы e1 и f1 можно всегда совместить. Тогда совпадут плоскости векторов e1 ,e2 и f1 , f2 . Поворачивая эту плоскость вокруг направления e1 , всегда можно совместить векторы e2 и f2 . Так как базисы ортонормированные,
то, следовательно, e3 будет коллинеарен f3 .
Видно, что возможны два случая: e3 f3 и e3 f3 .
В первом случае при помощи перемещения в пространстве базисы e1 ,e2 ,e3 и f1 , f2 , f3 совмещаются, а во втором случае нет.
Предположим, что эти базисы не совмещаются, т.е. e3 f3 и рассмотрим еще один ортонормированный базис g1 , g2 , g3 . Совершая описанную выше процедуру совмещения, мы получим, что этот базис совпадает либо с базисом e1 ,e2 ,e3 , либо с базисом f1 , f2 , f3 . Таким образом, множество всех ортонормированных базисов распадается на два класса. Базисы, принадлежащие одному классу, совмещаются друг с другом перемещением, а базисы, принадлежащие различным классам, не совмещаются. Эти классы называются классами ориентации или просто
ориентацией базисов.
Результат: Базисов много, ориентаций – две.
135
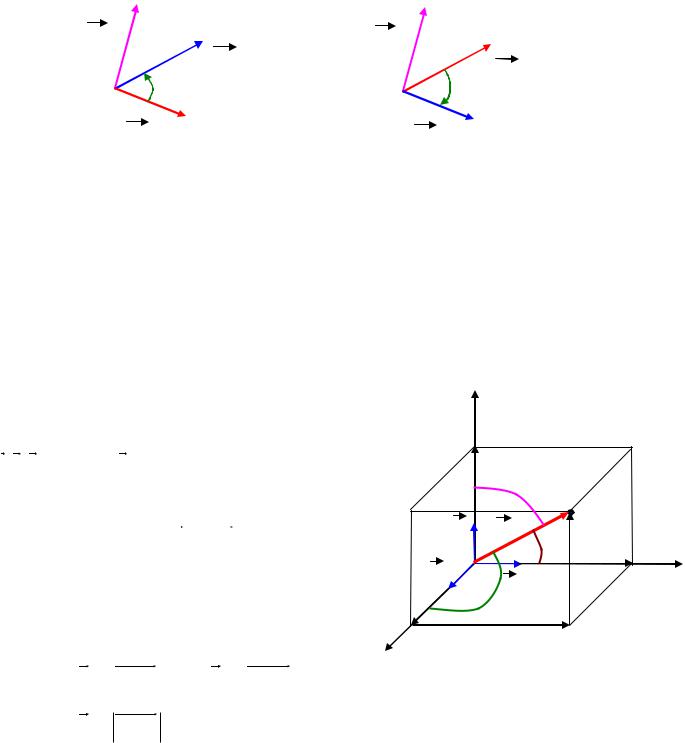
Определение 8.23. Упорядоченная тройка некомпланарных векторов в пространстве называется правоориентированной (или правой), если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае, тройка называется левоориентированной (или
левой). (Рис. 8.14а,б).
e3 |
|
|
|
|
|
|
|
|
|
e3 |
|
||
e1 |
e2 |
e1 |
||||
|
|
|
||||
|
|
|
||||
|
|
|
|
|||
|
|
|||||
|
|
|
|
e2 |
||
Рис. 8.14а. |
|
|
Рис. 8.14б. |
|||
Правая тройка. |
|
|
Левая тройка. |
|||
Выбрав базис, мы пространство превращаем в ориентированное пространство.
8.6. Разложение вектора по ортонормированному базису. Длина
вектора. Направляющие косинусы вектора.
8.6.1. Разложение вектора по ортонормированному базису.
Пусть в пространстве задана ДПСК |
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Охyz с ортонормированным |
базисом |
|
|
|
|
|
M3 |
|
|
|
|
||||||||||||||||
i, j, k . Пусть |
a - произвольный вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|||||
пространства. |
Совместим |
его |
начало |
с |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
началом координат: |
a OM (Рис. |
8.15). |
|
|
k |
a |
|
|
|
|
|
|
|||||||||||||||
|
|
|
β |
|
|
|
|||||||||||||||||||||
|
|
O |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M1 , M 2 , M3 - |
проекции |
точки |
М |
на |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
j |
|
|
M2 |
y |
||||||||||||||||||||||
|
|
α |
|
|
|
|
|||||||||||||||||||||
координатные |
оси |
Ox, |
Oy, |
|
|
|
Oz |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
соответственно. Тогда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||
прOx a |
|
OM1 |
|
, прOy a |
|
OM 2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Рис. 8.15. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прOz a OM 3 .
136
