Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Модуль 2 Векторная алгебра

.pdf

Скачиваний:

Добавлен:

30.03.2015

Размер:

758 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Из прямоугольного параллелепипеда получим a OM1 M1P PM , откуда

a OM1 OM 2 OM3 .

Т.к. OM1

OM1

i , OM 2

OM 2

j ,

OM 3

k , то

OM1

OM 2

OM3

k .

(8.3)

Обозначим через ax , ay , az проекции вектора a OM на координатные оси Ox,

Oy, Oz соответственно: ax

OM1

, ay

OM 2

OM 3

Тогда выражение

(8.3) примет следующий вид:

a ax i ay j az k .

(8.4)

По теореме 8.3. представление вектора a в виде (8.4) единственно.

Определение 8.24. Представление

вектора

в виде

(8.4) называется

разложением вектора a по ортонормированному базису i, j, k .

ax , ay , az - координаты вектора a в базисе i, j, k , т.е. a ax , ay , az .

8.6.2. Длина вектора. Направляющие косинусы вектора.

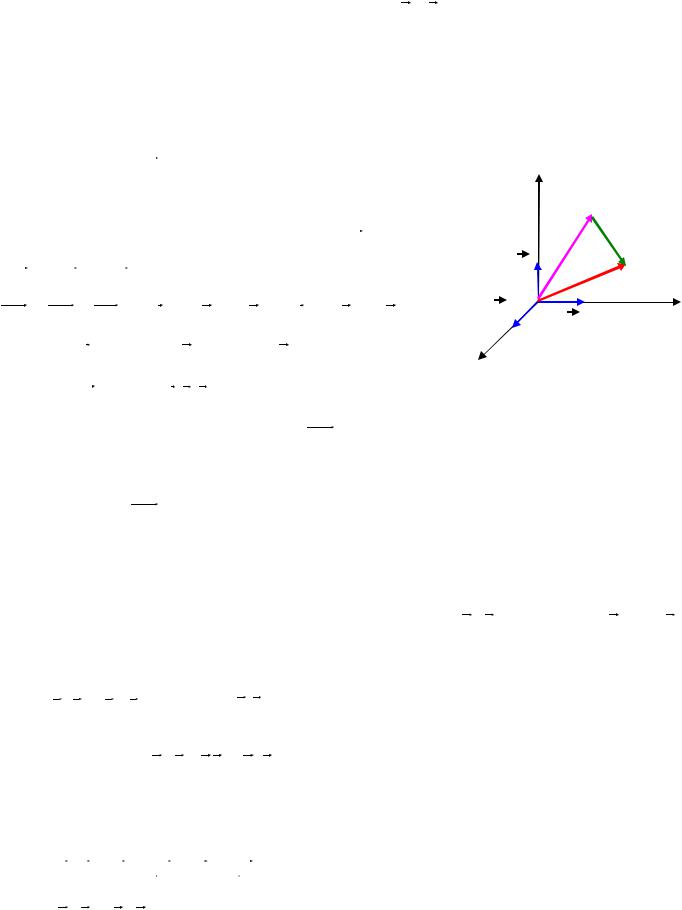
Найдем длину вектора a . Из прямоугольного параллелепипеда (Рис. 8.15)

2 a2

имеем

, т.е.

. Окончательно

ax2

ay2 az2 .

(8.5)

Пример 8.3. Найдите длину вектора a 2i 3 j k .

Решение. ax 2, ay 3, az 1. По формуле (8.5) имеем:

22 32 1 2

14 .

Ответ.

Пусть , , - углы между вектором a 0 и координатными осями Ox, Oy, Oz

соответственно. По теореме 8.1. имеем

cos , ay

cos , az

cos .

(8.6)

Из выражения (8.6) получим:

137

cos

, cos

(8.7)

Определение 8.25. Числа cos , cos , cos

называются

направляющими

косинусами вектора a .

Подставив

выражения

(8.6) в

равенство

2 a2 a2

a2 ,

получим

следующее важное соотношение:

cos2 cos2 cos2 1.

(8.8)

Таким образом, направление вектора в заданной системе координат

определяется его направляющими косинусами.

Легко видеть, что координатами единичного вектора

являются

направляющие косинусы: e (cos , cos , cos ) .

Пример 8.4. Найдите направляющие косинусы вектора a 2i 3 j k .

2, ay

3, az

Решение.

14 . По формуле (8.7) имеем:

cos

, cos

8.7. Действия над векторами в координатной форме.

Пусть даны векторы a ax , ay , az ,		b bx , by , bz в координатной форме.
1.	Линейные операции над векторами в координатной форме.
Предложение 8.3. Справедливы следующие свойства:
1.	a b ax bx , ay by , ay by ;	2. a ax , ay , az .
Доказательство. 1. a b ax i ay		j az k bx i by j bz k
ax bx i ay by j az bz k ax bx , ay by , ay by .
2.	a ax i ay j az k ax i ay j az k ax , ay , az .
2.	Равенство векторов: a b ax	bx , ay by , az bz .
	138

	Условие коллинеарности двух векторов: a \|\| b	ax	ay	az
3.					.
		bx	by	bz
4.	Координаты вектора.

Пусть в пространстве задана ДПСК Охyz и М – произвольная точка.

Определение 8.26. Координатами точки М называются координаты ее

радиус-вектора OM .
Пусть даны две точки	A x1 , y1 , z1 ,		B x2 , y2 , z2		z	A
Пусть даны две точки	A x1 , y1 , z1 ,		B x2 , y2 , z2			A
(Рис. 8.16). Найдем координаты вектора			AB . Имеем
OA AB OB . Откуда получим:					k	B
OA AB OB . Откуда получим:					O
AB OB OA x2 i y2 j z2 k x1i y1 j z1 k
				i
				i	j	y
x2 x1 i y2 y1 j z2	z1 k	-	разложение x		j	y
x2 x1 i y2 y1 j z2	z1 k	-	разложение x		Рис. 8.16.
					Рис. 8.16.
вектора AB в базисе i, j, k .
Таким образом, если	вектор	AB	задан началом	A x1 , y1 , z1		и концом

B x2 , y2 , z2 , то его координаты равны разностям соответствующих координат его конца и начала: AB x2 x1, y2 y1, z2 z1 .

8.8. Скалярное произведение векторов, его свойства.

8.8.1. Определение скалярного произведения.

Определение 8.27. Скалярным произведением a b векторов a и b

называется число, равное произведению длин этих векторов на косинус угла между



ними: a b	a	b			(8.9)
ними: a b	a	b	cos , a,b .		(8.9)

Обозначение: a b , ab ,				a, b .

8.8.2. Свойства скалярного произведения.

Предложение 8.4. Скалярное произведение обладает следующими свойствами:

1. a b

прb a

прa b ,

(8.10)

2. a b b a (коммутативность),

139

3.a b c a b a c ,

4.a b a b , R ,

5.a2 a 2 ,

6.a b 0 a b .

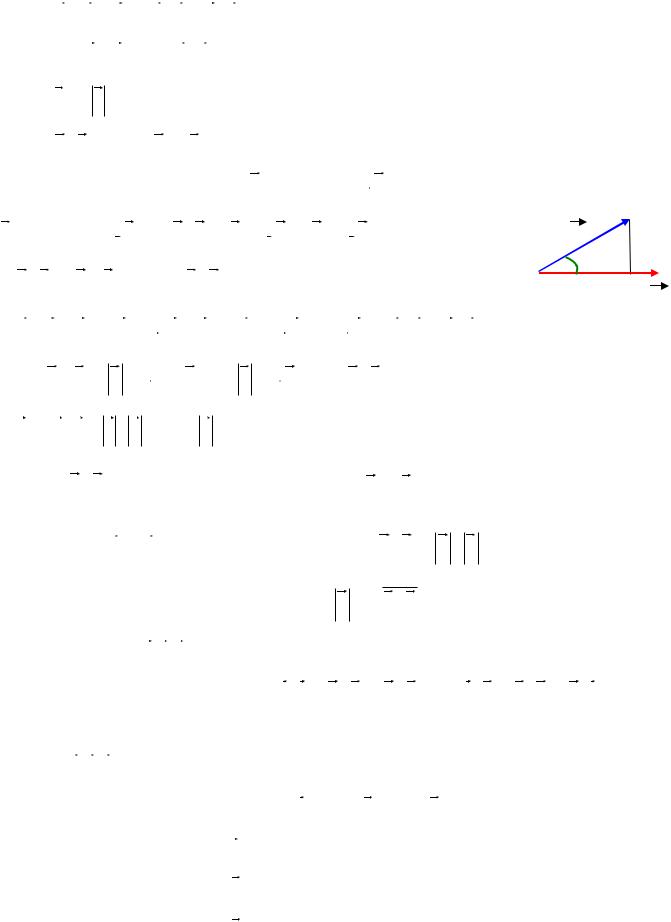
Доказательство. 1. Т.к.

cos прb a (Рис. 8.17)

cos прa b , то a b

прb a

прa b .

a b

cos b a .

a b c

прa b c

прa b прa c a b a c .

Рис. 8.17.

4. a b b прb a b прb a a b .

5. a2 a a a a cos0 a 2 .

6. Пусть a b 0 cos 0 a b .

Теперь пусть a b		cos 0 a b a b 0 0 .
	2

Замечание. Из свойства 5 имеем, что a a a .

Пусть задан i, j, k - ортонормированный базис. Используя свойства 5	и 6,
получим для базисных векторов i i j j k j 1, i j j k k i 0 .	Для

наглядности составим таблицу вычисления скалярного произведения базисных векторов i, j, k :

	i		j	k

i	1		0	0
i

j	0		1	0
j

k	0		0	1
k

		140

8.8.3. Вычисление скалярного произведения (в координатной форме).

Пусть в пространстве задана ДПСК с ортонормированным базисом i, j, k . Пусть

заданы векторы a ax i ay j az k ,

b bx i by j bz k . Найдем скалярное

произведение этих векторов:

a b ax i ay j az k bx i by j bz k axbx ii axby i j axbz ikaybx ji ayby j j aybz jk azbx ki azby k j azbz k k axbx ayby azbz ,

a b axbx

ayby azbz .

(8.11)

8.8.4. Некоторые приложения скалярного произведения.

1. Длина вектора.

Пусть задан вектор a ax , ay , az . Подставив (8.11) в равенство

a a ,

получим формулу для вычисления длины вектора a ax , ay , az :

a2 a2 a2 .

(8.12)

2. Угол между двумя векторами.

Пусть

заданы

ненулевые

векторы a ax , ay , az ,

b bx , by , bz . Из

определения

скалярного произведения

a b

cos имеем

cos

Используя формулы (8.11) и (8.12), получим:

cos

axbx ay by az bz

(8.13)

b2 b2

3. Условие перпендикулярности ненулевых векторов.

Из (8.13) получим условие перпендикулярности векторов

a ax , ay , az ,

b bx , by , bz :

a b axbx ayby az bz

0 .

(8.14)

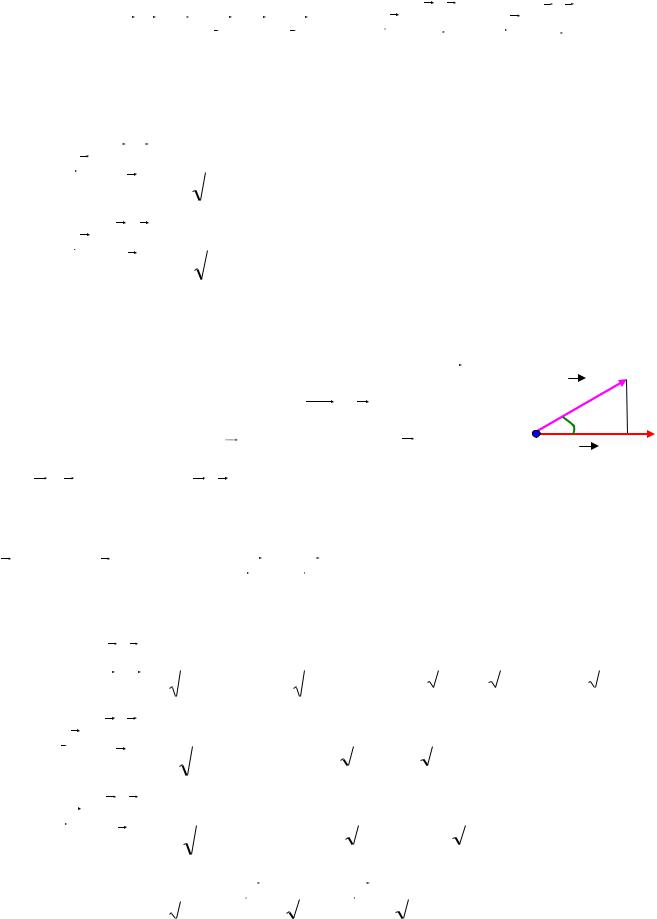
4. Проекция вектора на направление другого вектора.

141

пр a

Так как a b

пр

пр b , то

пр

. Используя

(8.11) и (8.12), получим формулы для вычисления проекции вектора на направление другого вектора:

пр b

a b

axbx ayby

azbz

(8.15)

пр a

a b

axbx ayby

azbz

(8.16)

5. Работа постоянной силы.

Пусть материальная точка перемещается прямолинейно из положения А в

положение

под

действием

постоянной

силы

F ,

AB S (Рис. 8.18).

образующей угол φ с перемещением

Известно, что работа силы F при перемещении S равна

A F S .

cos , т.е.

Рис. 8.18.

Пример

8.5.

Найдите

угол

между

векторами

a 2,1,0 ,

b 1, 1,3 и прa b ,

прb a .

Решение.

2, ay

1, az

0 ,

1, by

1, bz

cos

a b

axbx ay by az bz

2 1

ax2 ay2 az2

bx2 by2 bz2

4 1 1 1 9

прa b

a b

axbx ayby azbz

2 1

ax2 ay2 az2

4 1

прb a

a b

axbx ayby azbz

2 1

bx2 by2 bz2

1 1 9

Ответ. cos

, пр

пр a

142

Пример 8.6. Вычислите работу, произведенную силой F 4,2,3 , если точка ее приложения перемещается прямолинейно из положения A 2;4;6 в положение

B 3;5;7 . Под каким углом к АВ направлена сила F ?

Решение. S AB 1;1;1 . Значит, A F S 4 2 3 9 (ед. работы).

Найдем угол φ между векторами F и S по формуле:

cos	F S			9				9		9	, arccos		9	.
cos											, arccos			.
	F	S	16	4 9 1 1 1				29	3	87		87
						9
Ответ. A 9			(ед.работы), arccos			9	.

					87
					87

8.9. Векторное произведение векторов, его свойства.

8.9.1. Определение векторного произведения.

Определение 8.28. Векторным произведением вектора a на вектор b

называется вектор c , удовлетворяющий условиям:

1) c a, c b (вектор c перпендикулярен каждому из векторов a и b );

2)c a b sin , где φ – угол между векторами a и b ;

3)упорядоченная тройка векторов a , b , c образует правую тройку.

Обозначение. c a b или c a, b .

Замечание. Приведенные условия однозначно определяют векторное произведение, если векторы a и b - неколлинеарны. Если a , b - коллинеарны, то векторное произведение по определению есть нулевой вектор.

Замечание. Векторное произведение определяется только в трехмерном ориентированном пространстве.

8.9.2. Геометрический смысл векторного произведения.

Из условия 2 определения 8.28. вытекает важное геометрическое следствие:

векторное произведение a b по абсолютной величине численно равно площади

143

параллелограмма, построенного		на векторах	a	и b :
a b a b sin Sпар . (Рис. 8.19).					axb		b
							b

Предложение 8.4. Справедлива следующая формула:							φ	Sпар
Предложение 8.4. Справедлива следующая формула:							φ
a b	a 2 b 2 a b 2 .	(8.17)						a
							Рис. 8.19.
Доказательство.
a b 2 a 2	b 2 sin 2 a 2 b 2 1 cos2
	a 2	b 2 a 2 b 2	cos2 a 2		b 2	a b 2 .

Пример 8.7. Найдите, используя формулу (8.17), площадь параллелограмма,

построенного на векторах

a 1, 1,2 ,

b 0, 1,0 .

Решение.

2 6;

1; a b 1. Подставив полученные значения в

(8.17),

2 a b 2

получим: Sпар

a b

36 1 35 .

Ответ. Sпар

35 .

8.9.3. Свойства векторного произведения.

Предложение 8.6. Справедливы следующие свойства векторного произведения:

1)a b b a (антикоммутативность),

2)a b c a c b c ,

3)a b a b , R ,

4)a b 0 a || b.

Доказательство. 1) Векторы a b

и b a - коллинеарны, имеют одинаковую

длину, противоположно направлены,

так как тройки a , b , a b и

a , b ,b a

образуют противоположные ориентации. Следовательно, a b b a .

4) Необходимость. Пусть a b 0

a b

sin 0

или

0 ,

или sin 0 . В первом и втором случаях один из сомножителей – нулевой вектор.

a || b. Если sin 0 , то 0 или , откуда следует a || b.

144

Достаточность. a || b 0 или sin 0 a b 0 a b 0.

Из свойств 2 и 3 векторного произведения получим соотношение, называемое

свойством линейности векторного произведения по первому сомножителю:

a b c a c b c , , R .

Векторное произведение линейно и по второму сомножителю.

Пусть задан i, j, k - ортонормированный базис. Из определения векторного произведения вытекают следующие соотношения для базисных векторов: i j k ,

j k i , k i j . Пользуясь свойством 1 векторного произведения, получим еще

три равенства: j i k , k j i , i k j . Из свойства 4 имеем:

i i j j k k 0 . Для наглядности составим таблицу вычисления векторного

произведения базисных векторов i, j, k			(векторы левого столбца умножаются на
соответствующие векторы верхней строки):

		i		j		k

	i	0		k		- j

	j	- k		0		i

	k	j		- i		0
							i
Удобно пользоваться следующей			схемой		(Рис. 8.20): если		i
направление кратчайшего пути от первого вектора ко второму
совпадает с направлением стрелки, то				векторное произведение k			j
равно третьему вектору, если не совпадает – третий вектор берется							Рис. 8.20.
							Рис. 8.20.

со знаком «минус».

8.9.4. Вычисление векторного произведения (в координатной форме).

Пусть в пространстве задана ДПСК с ортонормированным базисом i, j, k . Пусть

заданы векторы a ax i ay j az k ,

b bx i by j bz k . Найдем векторное

произведение этих векторов:

145

a b a i a j a k b i b j b k

axbx i i axby i j axbz i k aybx j i ayby j j

aybz j k azbx k i azby k j azbz k k

0 axby k axbz j aybx k 0 aybz i azbx j azby i 0

aybz azby i axbz azbx j axby aybx k .zz x yx y

Легко видеть, что aybz azby i axbz azbx j axby aybx k

Окончательно получим формулу для вычисления векторного произведения:

	i	j	k
a b	ax	ay	az	.	(8.18)
	bx	by	bz
Пример		8.8.	Вычислите векторное произведение векторов		a 1,2,0 ,

b 2,3, 5 .

Решение. Используя формулу (8.18), получим:

	i	j	k
a b	1	2	0	10i ( 5) j ( 1)k 10i 5 j k 10,5, 1 .
	2	3	5

Ответ. a b 10,5, 1 .

8.9.5. Некоторые приложения векторного произведения.

1. Нахождение площади параллелограмма и треугольника.

Площадь параллелограмма, построенного на векторах a и b , вычисляется по формуле: Sпар a b . Площадь треугольника, построенного на векторах a и b ,

вычисляется по формуле: Sтреуг 12 Sпар 12 a b . 146

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.03.20162.2 Mб49Моделирование - Лекция.pdf
#
13.03.20161.08 Mб27Моделирование - Нелинейные уравнения.pdf
#
13.03.2016786.52 Кб17Моделирование - Эмпирические модели.pdf
#
30.03.201589.6 Кб12модель смарт.doc
#
30.03.20151.83 Mб129Модуль 1 Линейная алгебра.pdf
#
30.03.2015758 Кб20Модуль 2 Векторная алгебра.pdf
#
30.03.201559.98 Кб18Модуль 2.docx
#
30.03.2015176.94 Кб4моё-1.docx
#
30.03.2015229.63 Кб6моё.docx
#
25.12.2018330.24 Кб9мои ответы.doc
#
03.12.20184.22 Mб30мой kursov.doc