
Модуль 2 Векторная алгебра
.pdf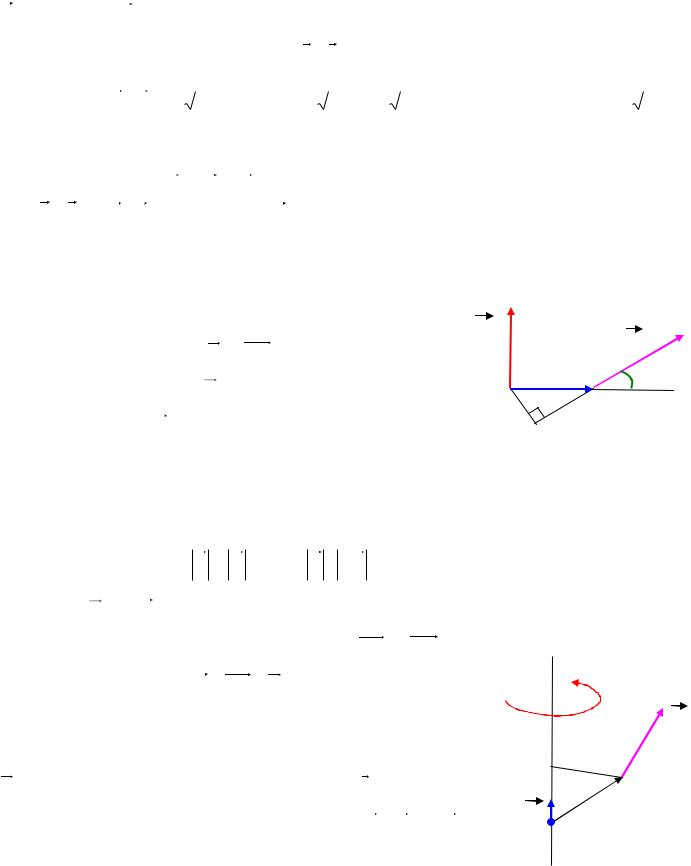
Пример 8.9. Найдите |
площадь |
|
треугольника, |
построенного |
на векторах |
||||||||||||||||||||||||||||||||||||
a 1,2,0 и b 2,3, 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. Из примера 8.8 имеем: a b 10,5, 1 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
S |
треуг |
|
|
a b |
|
|
100 25 1 |
|
|
126 |
|
14 . |
|
Ответ. S |
треуг |
|
14 . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2. Условие коллинеарности векторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
j |
k |
|
|
|
|
a |
|
|
|
ay |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a || b a b |
a |
|
|
a |
|
a |
|
0 |
x |
|
|
|
z |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bx |
bz |
|
|
|
bz |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
bx |
by |
bz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. Нахождение момента силы относительно точки. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Пусть в пространстве заданы точки А и М. Пусть в |
m |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB (Рис. 8.21). Известно, |
|
|
|
F |
|
|
|||||||||||||||||||||
точке А приложена сила F = |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
|
что моментом |
силы |
F |
относительно |
точки |
М |
M |
A |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
называется вектор m , который: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|||||||||||||||
1) проходит через точку М, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.21. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2)перпендикулярен плоскости, проходящей через точки М, А, В,
3)численно равен m F MN F MA sin , где MN – плечо, φ – угол между
векторами F и MA ,
4) образует правую тройку с векторами MA и AB .
Откуда имеем, что m = MA F .
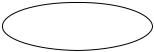
4. Нахождение линейной скорости вращения.
Пусть твердое тело вращается с угловой скоростью
вокруг неподвижной оси. Скорость v точки М
твердого тела находится по формуле Эйлера: v OM ,
где О – некоторая неподвижная точка оси (Рис. 8.22).
147
v
 M
M
ω
O
Рис. 8.22.
8.10. Смешанное произведение векторов, его свойства. |
|
|
|||||||
8.10.1. Определение смешанного произведения. Геометрический смысл |
|||||||||
смешанного произведения. |
|
|
|
|
|
|
|||
Определение 8.29. Смешанным произведением векторов a , b , c называется |
|||||||||
число, равное скалярному произведению вектора a на вектор b c . |
|
|
|||||||
Обозначение: a b c , abc или a,b,c . |
|
|
|
|
|
||||
Теорема 8.4. (Геометрический смысл смешанного произведения) Смешанное |
|||||||||
произведение |
некомпланарных |
векторов a , b , c по |
модулю |
равно |
объему |
||||
параллелепипеда, построенного на сомножителях. Оно положительно, если тройка |
|||||||||
a , b , c – правая, и отрицательно, если тройка |
a , b , c – левая. |
|
|
||||||
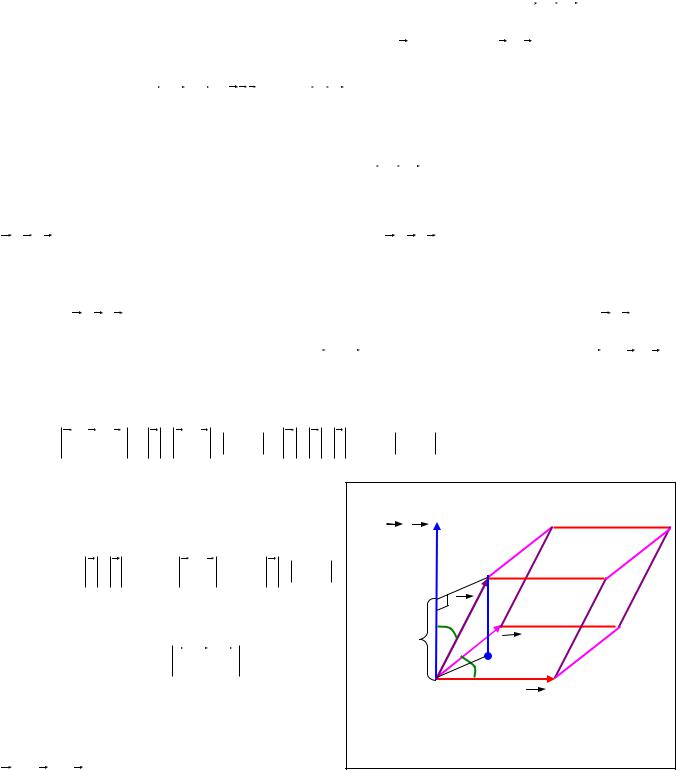
Доказательство. Построим параллелепипед, ребрами которого являются |
|||||||||
векторы a , b , c , основанием – параллелограмм, построенный на векторах b , c (Рис. |
|||||||||
8.23). Здесь φ – угол между векторами b и c ; |
θ - угол между векторами a и b c . |
||||||||
С одной стороны, по определению скалярного и векторного произведения |
|||||||||
имеем: |
a b c a b c cos |
a b c sin cos . |
|
|
|
||||
С |
другой |
стороны, |
объем |
|
|
|
|
|
|
параллелепипеда равен Vпаралл да |
Sосн h , |
bxc |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
где Sосн. b c sin b c , h a cos |
|
|
|
|
|
||||
- высота параллелепипеда. |
|
|
|
a |
|
|
|||
|
|
|
h |
|
|
||||
|
|
|
a b c Vпаралл да . |
|
|
|
|
||
Следовательно, |
h |
θ |
c |
|
|
||||
|
|
φ |
|
|
|||||
Итак, получили, что смешанное |
|
|
b |
|
|
||||
|
|
|
|
|
|||||
произведение |
некомпланарных |
векторов |
|
|
Рис. 8.23. |
|
|
||
|
|
|
|
|
|
|
|
|
|
a , b , c по модулю равно объему |
|
|
|
|
|
||||
параллелепипеда, построенного на сомножителях. |
|
|
|
|
|||||
148

Теперь докажем, что смешанное произведение положительно, |
если тройка |
|||||||||||||||
a , b , c – правая, и отрицательно, если тройка a , b , c – левая. |
|
|||||||||||||||
Из равенства |
|
a b c |
|
|
a |
|
|
|
b c |
|
|
|
cos |
|
видно, что знак |
смешанного |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
произведения совпадает со знаком cos . Смешанное произведение положительно,
когда вектор |
a направлен в ту же сторону от плоскости векторов b и c , что и |
вектор b c , |
т.е. тройка a , b , c - правая тройка. Аналогично доказывается, что |
смешанное произведение левой тройки отрицательно. |
|
Предложение 8.7. Справедливы следующие свойства смешанного |
|
произведения: |
|
1). Векторы a , b , c компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е. a,b,c =0.
2). Смешанное произведение не меняется при циклической перестановке его сомножителей: a b c = b c a = c a b .
3). Смешанное произведение не меняется при перемене местами знаков скалярного и векторного умножения: a b c = a b c .
4). Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей: a,b,c b,a,c b,c,a c,b,a c,a,b a,c,b .
5). Смешанное произведение линейно по первому сомножителю:
a1 a2 ,b,c a1 ,b,c a2 ,b,c .
(Аналогично имеет место линейность смешанного произведения по второму,
третьему сомножителю).
Доказательство. 1). Необходимость. Пусть a,b,c компланарны. Тогда вектор b c будет перпендикулярен плоскости, в которой лежат векторы a , b , c . Значит, b c перпендикулярен вектору a , откуда имеем: a b c =0, т.е. a,b,c =0.
149

Достаточность. Пусть a,b,c =0. Равенство |
a,b,c |
|
a |
|
|
|
b |
|
|
|
c |
|
sin cos 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возможно в следующих случаях:
1.Хотя бы один из векторов нулевой, тогда векторы a,b,c компланарны,
2.sin =0, тогда b , c - коллинеарны. Значит, векторы a,b,c компланарны,
3.cos =0, тогда a b c . Значит, a параллелен плоскости векторов b , c . Это означает, что a,b,c компланарны. Свойство 1 доказано.
2). Данное свойство верно, так как в этом случае не меняется ни объем пераллелепипеда, ни ориентация его ребер.
3). Из свойства скалярного произведения имеем: a b c = c a b . По предыдущему свойству c a b = a b c . Окончательно имеем: a b c = a b c .
4). Верно в силу антикоммутативности векторного произведения и коммутативности скалярного произведения.
5) Доказывается с использованием свойства линейности скалярного произведения.
8.10.2. Вычисление смешанного произведения (в координатной форме).
Пусть в пространстве задана ДПСК с ортонормированным базисом i, j, k . Пусть
заданы векторы a ax i ay j az k , b bx i by j bz k , c cx i cy j cz k .
Найдем смешанное произведение этих векторов, используя выражения в координатах для скалярного и векторного произведений:
a b c ax i ay j az k |
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
||||||
bx |
|
by |
|
bz |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
cx |
|
cy |
|
cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
i |
|
b |
b |
|
j |
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a i a j a k |
|
|
y |
z |
|
|
x |
z |
|
|
x |
|
y |
k |
|||||||
x |
y |
z |
|
|
cy |
cz |
|
|
|
cx |
cz |
|
|
|
cx |
cy |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
||

a |
|
by |
|
bz |
|
a |
|
bx |
bz |
|
a |
|
bx |
by |
|
|
ax |
ay |
az |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
b b |
|
b |
. |
|
|
|
|
||||||||||||||||||
|
x |
cy |
|
cz |
|
|
y |
cx |
cz |
|
|
|
z |
cx |
cy |
|
|
|
x |
|
y |
|
z |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cx |
cy |
cz |
|
|
|
|
|
||
Итак, смешанное |
|
произведение векторов a ax , ay , az , |
b bx , by , bz , |
|||||||||||||||||||||||||||||
c cx , cy , cz вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a, b, c |
|
ax |
ay |
|
az |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
bx |
by |
|
bz |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.19) |
|||||||||
|
|
|
|
cx |
cy |
|
cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 8.10. Вычислите |
смешанное |
|
|
произведение векторов a 1,2,0 , |
||||||||||||||||||||||||||||
b 2,3, 5 , c 1,0,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Используя формулу (8.19), получим: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a, b, c |
|
ax |
ay |
az |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 0 |
|
|
||||||||||||
|
|
|
|
|
1 2 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
bx |
by |
bz |
|
|
2 |
|
3 |
5 |
II 5 III |
3 |
3 |
0 |
|
9 . |
|||||||||||||||||
|
|
|
|
|
|
cx |
cy |
cz |
|
|
|
|
1 0 1 |
|
|
|
|
|
|
|
1 0 1 |
|
|
|||||||||
Ответ. a, b, c 9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8.10.3. Некоторые приложения смешанного произведения. |
|
|
|
|
||||||||||||||||||||||||||||
1. Определение взаимной ориентации векторов в пространстве. |
|
|||||||||||||||||||||||||||||||
Если |
a, b, c 0 , |
то a , b , c – |
правая тройка, |
если |
a, b, c 0 , |
то a , b , c – |
||||||||||||||||||||||||||
левая тройка. |
|
|
|
|
2. Условие компланарности векторов: |
|
|
|
|
|
|
|
|
|
Векторы a , b , c компланарны a, b, c 0 |
ax |
ay |
az |
|
bx |
by |
bz |
0 . |
|
|
cx |
cy |
cz |
|
|
|
|
|
|
3. Нахождение объемов параллелепипеда и треугольной пирамиды.
Объем параллелепипеда, построенного на векторах a , b , c , равен модулю смешанного произведения этих векторов: Vпаралл да = a,b,c .
151

Объем треугольной пирамиды, построенной на векторах a , b , c , вычисляется по формуле: Vпирам = 16 a,b,c .
Пример 8.11. Определите ориентацию векторов: a 1,2,0 , b 2,3, 5 , c 1,0,1 .
Решение. Из примера 8.10. имеем: a, b, c 9 . Значит, упорядоченная тройка
векторов a , b , c является правоориентированной (правой). |
|
|||||||||
Ответ. a , b , c - правая тройка. |
|
|
|
|
||||||
Пример 8.12. Проверьте, компланарны ли векторы: a 1,2,0 , |
b 2,4,0 , |
|||||||||
c 1,0,1 . |
|
|
|
|
|
|
|
|
||
Решение. Если a, b, c 0 , то векторы a , b , c - компланарны. Вычислим |
||||||||||
a, b, c |
|
ax |
ay |
az |
|
|
2 |
0 |
|
|
|
|
1 |
|
|
||||||
|
bx |
by |
bz |
|
2 |
4 |
0 |
0 векторы a , b , c - компланарны. |
||
|
|
cx |
cy |
cz |
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. Векторы a , b , c - компланарны. |
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 8.13. Найдите |
объем |
параллелепипеда, построенного на |
векторах |
|||||||||||||||||
a 1,2,0 , b 3,1,5 , |
c 2,1,0 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Vпаралл да = |
|
a,b,c |
. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a, b, c |
|
ax |
ay |
|
az |
|
|
2 |
0 |
|
|
|
a,b,c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
bx |
by |
|
bz |
|
3 |
1 |
5 |
5 |
Vпаралл да = |
|
|
|
5 |
|
|
5 . |
|||
|
|
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
cx |
cy |
|
cz |
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. Vпаралл да =5.
152

№272. По данным векторам a , b постройте векторы:
1)3a 12 b , 2) a 4b , 3) 2 a b , 4) 23 a 2b a b .
№273. Дан треугольник АВС, М – точка пересечения медиан
треугольника, AM a , AC b . Разложите AB и BC по векторам a , b .
№ |
274. |
Даны |
две точки A 2,1, 1 , |
B 3, 4,1 . Найдите координаты |
||
векторов AB и BA . |
|
|
|
|||
№ 275. Даны вершины |
A 1, 2,3 , B 3,2,1 , |
С 6,4,4 параллелограмма |
||||
ABCD. Найдите координаты вершины D. |
|
|
||||
№ |
276. |
При |
каких |
значениях |
, |
векторы a i 6 j 2k , |
b 2i 3 j k коллинеарны? |
|
|
||||
№277. Разложите вектор c 9,4 по векторам a 2, 3 и b 1,2 .
№278. Представьте вектор d 4,12, 3 в виде линейной комбинации векторов a 2,3,1 , b 5,7,0 , b 3, 2,4 .
153
