2. Математические модели сау

Математические модели САУ представляются в виде дифференциальных уравнений. Существует два подхода к составлению математических моделей САУ:

- в переменных «вход – выход»;

- в переменных состояния.

При рассмотрении математических моделей в переменных «вход – выход» часто используют символическую форму записи линейных дифференциальных уравнений. Например, пусть дифференциальное уравнение, описывающее поведение САУ, имеет вид

, (1)

где y(t) - выходной сигнал;

u(t) - входной (управляющий) сигнал;

f(t) - помеха, действующая на САУ.

Введём для операции дифференцирования обозначение «р», т.е. , при этом- символ интегрирования.

Используя этот символ, дифференциальное уравнение (1) примет вид

. (2)

При использовании символ р и необходимо иметь в виду, что они допускают следующие математические операции: сложение, вычитание, умножение, возведение в целую степень. Арифметические действия с символами р иобладают свойством дистрибутивности и не обладают свойством коммутативности в отношении функции времени, к которым применён символ «р».

Свойство дистрибутивности позволяет выносить за скобки функцию времени, образовывать полиномы и дробно-рациональные функции символа «р».

Учитывая это свойство, запишем уравнение (2) в виде

(3)

Введем следующие обозначения:

- собственный оператор;

- операторы воздействия.

Передаточная функция в операторной форме – это отношение оператора воздействия к собственному оператору:

- передаточная функция по управляющему воздействию;

- передаточная функция по возмущающему воздействию.

Используя передаточные функции, исходное уравнение можно записать в виде

(4)

Индексы у передаточной функции обычно обозначают входной и выходной сигналы.

Если линейная САУ имеет несколько входов, то при определении передаточной функции относительно одной входной величины остальные полагаются равными нулю.

Довольно часто передаточная функция записывается в форме изображения Лапласа, т.е. отношение изображения выходной величины к изображению входной величины при нулевых условиях.

Преобразование Лапласа даёт соответствие между вещественным переменным x(t) (оригинал) и функцией комплексного переменного – изображение – X(s), . Иногда используется символическая запись:

,

где L - оператор Лапласа.

Применим преобразование Лапласа к уравнению (1):

.

Используя свойства преобразования Лапласа при нулевых начальных условиях, получим

(5)

Из соотношений (5) имеем:

Таким образом, передаточные функции в форме изображения Лапласа с точностью до обозначений совпадают с передаточными функциями в операторной форме. Это сходство передаточных функций чисто внешнее и является справедливым только для стационарных линейных систем.

Передаточные функции являются одним из основных инструментов для изображения структурных схем (рис. 9).

Рис. 9

Представление математических моделей САУ в переменных «входы - выходы» имеет в основном технические преимущества: исследователь имеет дело с переменными, имеющими физический смысл, и имеет возможность сопровождать теоретические исследования экспериментом. Однако, при таком представлении математические описания различных систем и блоков являются разнотипными в зависимости от порядков числителей и знаменателей их передаточных функций.

Более единообразное математическое описание САУ можно получить, если ввести вместо выходных переменных «y» другие переменные «х», получившие название «переменных состояния».

Описание системы в этих переменных даётся системой дифференциальных уравнений первого порядка, разрешённых относительно первых производных, т.е. уравнений в форме Коши

, (6)

где векторную переменную называют вектором состояния, а компоненты вектораx₁, x₂…x_n - переменными состояния.

Таким образом, состояние линейной САУ в данный момент времени однозначно характеризуется вектором состояния , удовлетворяющим дифференциальному уравнению:

(7)

где A(t), B(t) и C(t) - матрицы размера nn, mn и nr (mn, rn);

- вектор входных воздействий;

- вектор начальных условий;

- вектор измерений.

Обычно предполагается, что векторно-матричное уравнение описывает объект управления, а уравнениехарактеризует тот факт, что измерить в реальной САУ удаётся только часть компонент вектора состояния.

Различные преобразования системы уравнений (7) связаны с действиями над матрицами, и в большинстве случаев нагляднее рассматривать эти преобразования с помощью структурных схем. Структурная схема это графическое условное изображение взаимосвязанных элементов или звеньев, составляющих систему и различающихся своими динамическими свойствами.

Рис. 10

На структурной схеме изображены следующие блоки (рис. 10):

- матричные блоки B(t), C(t), A(t) осуществляют линейное преобразование вектора входных сигналов в вектор выходных сигналов;

- интегрирующий блок, имеющий несколько входов и несколько выходов;

- суммирующий блок.

Вектор состояния определяется, как известно, выражением:

, (8)

где – матрица фундаментальных решений однородной системы, соответствующих (7).

Таким образом, математическая модель САУ в переменных состояния представляет собой совокупность уравнений первого порядка, допускающих получение в достаточной мере единообразных методов анализа и синтеза систем, а также алгоритмов для численных методов решения этих задач на ЭВМ.

При возникновении необходимости перехода от переменных «вход – выход» к переменным состояния могут быть получены уравнения в различной форме, т. к. разложение сложного звена на простейшие, как известно, не единственно.

В настоящее время в теории автоматического управления разработаны методы перехода к уравнениям в переменных состояния не только для систем с постоянными коэффициентами, но и для переменных коэффициентов и многосвязных систем. Кроме того, в ряде прикладных программ («Matlab» и др.) заложена возможность перехода от переменных «вход – выход» к переменным состояния и обратно.

Преобразование структурных схем

Математические модели САУ в переменных «вход – выход» обычно представляют в виде структурных схем, которые первоначально составляются в соответствии с принципом функционирования системы (рис. 11).

Приведем в качестве примера типичную следящую систему, в которой маломощное задающее воздействие отслеживается мощным исполнительным устройством – стабилизация ствола орудия, антенна радиолокатора и т.д.

Рис. 11

W₃, W_ус, W_к, W_дв, W_оу, W_ос - передаточные функции соответственно задающего устройства, усилителя, корректирующего звена, двигателя, объекта управления, датчика обратной связи;

(t) - угол поворота (входной сигнал);

U(t) - напряжение, пропорциональное (t);

f(t) - возмущение;

M_дв - момент;

(t) - угол поворота объекта управления (выходной сигнал);

U_oc - напряжение на выходе датчика обратной связи.

Передаточные функции каждого блока известны, но для дальнейшего

исследования структурную схему необходимо представить, например, в виде

рис. 12.

Рис. 12

Таким образом, необходимо производить эквивалентные преобразования структурных схем (эквивалентные, т.е. не нарушающие динамических свойств).

Для линейных стационарных систем существуют следующие правила преобразования структурных схем.

Последовательное соединение звеньев (рис. 13)

Рис. 13

Параллельное соединение звеньев (рис. 14)

Рис. 14

Контур с обратной связью (рис. 15)

Рис. 15

Перенос узла (точки разветвления сигнала) (рис. 16)

Рис. 16

Перенос точек суммирования (рис. 17)

Рис. 17

Типовые входные сигналы

Исследование динамических свойств САУ в большинстве случаев производится по анализу реакции САУ на типовые воздействия. Такими типовыми воздействиями являются ступенчатая функция, импульсная функция, гармоническая функция времени.

Ступенчатая функция:

(9)

где 1(t) - единичное ступенчатое воздействие.

Вид ступенчатой функции показан на рис. 18.

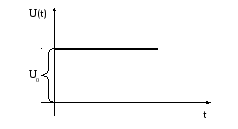
Рис. 18

Реакция САУ на ступенчатое воздействие называется переходной функцией h(t).

Функция h(t) характеризует переход системы из одного установившегося режима в другой. При построении h(t) принимают, как правило, u₀=1. Пусть передаточная функция САУ имеет в общем случае вид

(10)

Отыскание h(t) представляет собой процесс решения неоднородного дифференциального уравнения, вследствие чего

(11)

где

c_i - произвольные постоянные интегрирования;

_I - корни характеристического уравнения.

Для устойчивой САУ

т.е. теоретически время переходного процесса стремится к бесконечности.

Одним из способов построения переходного процесса является использование преобразования Лапласа.

Если учесть, что изображением ступенчатой функции будет

то решение неоднородного дифференциального уравнения равноценно определению оригинала по изображению .

Типичный вид переходного процесса показан на рис. 19.

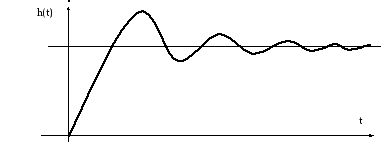
Рис. 19

Импульсная функция и (t) - функция

В этом случае

(12)

где

A - постоянная (обычно принимается А=1);

- импульс бесконечно большой величины и бесконечно малой длительности, так что.

Часто используется (t) - функция, которая в отличие от является двухсторонней и при этом

Путем предельного перехода вводится понятие производных

и т.д.,

Отметим также, что изображение . Реакция системы на импульсную функцию называется импульсной переходной функциейили весовой функцией(t).

Естественно, что и, соответственно, если найдена переходная функцияh(t) , то весовая функция находится путем дифференцирования, т.е.

(13)

Типичный вид импульсной переходной функции показан на рис. 20.

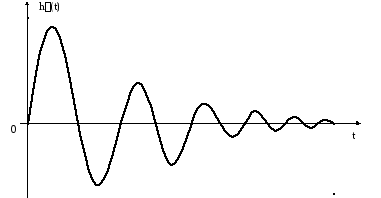
Рис. 20

Гармоническая функция времени

Входной сигнал в комплексной форме имеет вид

(14)

В этом случае рассматривается только частное решение неоднородного уравнения, соответствующего передаточной функции (10), которое отображает вынужденные установившиеся колебания.

Вынужденные колебания линейной стационарной САУ будут совершаться по гармоническому закону с той же частотой, что и входное воздействие u(t), но с амплитудой и фазой, отличающихся от амплитуды и фазы u(t).

Зависимость амплитуды и фазы выходного сигнала САУ от частоты определяются по амплитудно-частотным и фазочастотным характеристикам.

Частное решение дифференциального уравнения, соответствующего передаточной функции, при входном гармоническом сигнале имеет вид

Амплитудно-фазовая характеристика или комплексный коэффициент усиления определяется как отношение

т.е. амплитудно-фазовая характеристика может быть получена путём замены символа р на i в передаточной функции

(15)

Выражение W(i) можно записать в показательной форме

(16)

где - амплитудно-частотная характеристика;

() - фазочастотная характеристика.

Учитывая, что W(i) дробно-рациональная функция, W() равен отношению модулей числителя и знаменателя

(17)

где R - вещественная часть;

J - мнимая часть;

Фазочастотная характеристика определяется по выражению:

(18)

Представление W(i) в виде суммы действительной и мнимой частей даёт еще два вида частотных характеристик

(19)

где U() - вещественная частотная характеристика;

V() - мнимая частотная характеристика.

Очевидно, что

(20)

U() и V() вычисляются по выражениям

В теории автоматического управления широко используется графическое построение функции W(i) в комплексной плоскости U и iV при изменении  от «0» до «».

Вектор при изменении меняется по модулю и направлению, в результате чего конец вектора описывает кривую (годограф).

Если a₀0 и b₀0, то . Типичный вид амплитудно-фазовой характеристики показан на рис. 21.

Рис. 21

В теории САУ широко используются логарифмические частотные характеристики. При логарифмировании выражения получим

(21)

Вместо функции используется функция, которая называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Отметим также, что() - фазочастотная характеристика (ЛФЧХ), при этом в L() и () по оси абсцисс откладывается , но записывается значение и используются понятия изменения  в 2 раза (октава) и в 10 раз (декада).

По оси ординат для L() откладываются относительные логарифмические величины в децибелах (дБ), так, например, изменение амплитуды в 10 раз соответствует 20 дБ, в 100 раз – 40 дБ и т.д.

При построении ЛФЧХ по оси ординат фаза откладывается в обычном масштабе.

На рис. 22 показана логарифмическая шкала для ЛАЧХ.

lg

Рис. 22

В заключение этого раздела отметим, что если вычислена весовая функция (t), то реакцию САУ на входной сигнал произвольного вида можно определить с помощью интеграла Дюамеля (интеграла свёртки)

(22)