Уравнение поверхности и линии в пространстве

Пусть задана ДСК в пространстве. Уравнением поверхности называется такое уравнение с тремя переменными, которому удовлетворяют координаты каждой точки данной поверхности и не удовлетворяют координаты любой другой точки. Переменныеназываются текущими координатами точек поверхности.

Линию в пространстве можно рассматривать как линию пересечения поверхностей:

Плоскость описывается общим уравнением вида

,

где хотя бы один из коэффициентов отличен от нуля.

3. 4. Дано: точка , вектор.

Найти: уравнение плоскости, проходящей через точку перпендикулярно вектору.

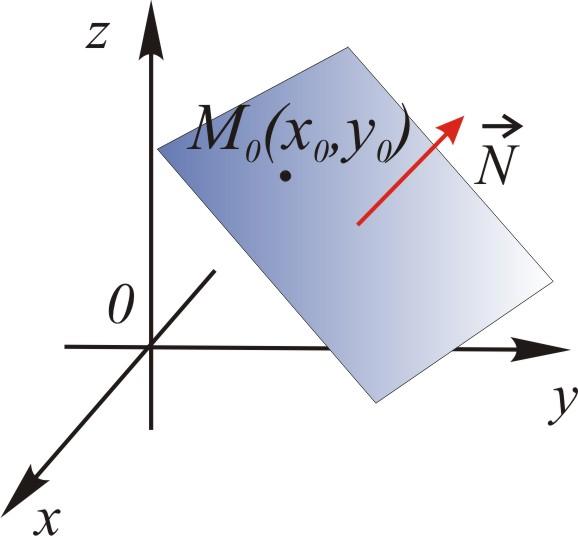
Решение. Выберем на плоскости произвольно точку с текущими координатами. Тогда векторперпендикулярен вектору. Т.е.. Получим

– уравнение плоскости по точке и нормали (любой ненулевой вектор, перпендикулярный плоскости, будем называть нормалью).

Приведем без доказательства еще два вида уравнений плоскости.

Уравнение плоскости, проходящей через точки (не лежащие на одной прямой):

.

Уравнение плоскости, отсекающей на осях координат ненулевые «отрезки» .

.

Замечания.

- Если в уравнении плоскости свободный член , то плоскость проходит через начало координат.

- Если в уравнении отсутствует какая-либо координата, то плоскость проходит параллельно соответствующей оси.

- Коэффициенты при в общем уравнении – координаты нормали плоскости.

- Уравнения координатных плоскостей имеют вид соответственно.

Построить плоскость по ее уравнению

1. . Все коэффициенты в уравнении отличны от нуля, поэтому удобно преобразовать его к уравнению в отрезках: .
2. . Уравнение не содержит переменную , значит, плоскость параллельна оси, и ее направляющей служит прямая.
3. . Это плоскость, параллельная осям и, иначе говоря, параллельная плоскости , проходящая «на высоте 3».

Прямая в пространстве задается каноническим, параметрическим или общим уравнениями.

1. Найдем уравнение прямой, проходящей через заданную точку параллельно заданному вектору.

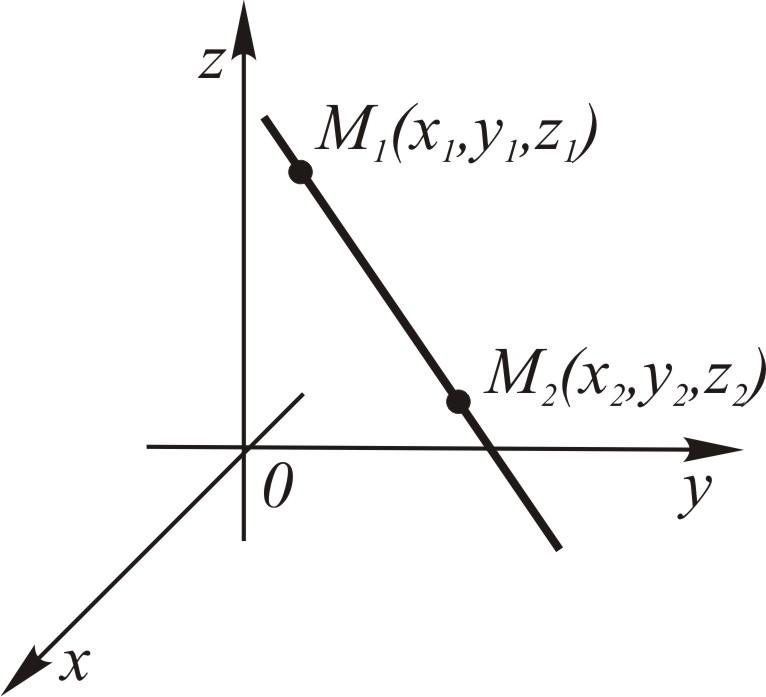
Выберем на прямой произвольно точку с текущими координатами. Тогда векторпараллелен вектору:

.

Это уравнение называется каноническим уравнением прямой в пространстве.

1а. Рассуждая аналогично, получим уравнение прямой по двум ее точкам :

.

2. Введем в каноническом уравнении параметр :

.

Уравнение прямой в таком виде называется параметрическим. При фиксированном значении параметра получаем соответствующую точку прямой. Придавая все значения из числового промежутка, получим соответствующий отрезок прямой.

3. Также прямую можно задать как линию пересечения непараллельных плоскостей.

Такое уравнение называется общим. Почему «альфа»???

Для решения задач, необходимо уметь переходить от одной формы записи прямой к другой.

Найти расстояние от точки до прямой. рис. Не такой!!!

Решение. Убедимся, что . Подставив ее координаты в уравнение прямой, мы видим:(если хотя бы одно из равенств не выполнено, то точка не принадлежит прямой). Обозначим– проекцияна. Тогда расстояние отдо

.

Точку найдем как пересечение заданной прямойи перпендикулярной к ней плоскости, проходящей через. Из рисунка видно, что вектор, направляющий прямую, является длянормалью, т.е. можно воспользоваться уравнением плоскости по точке и нормали:

.

Тогда .

Чтобы решить систему, предварительно приведем уравнение прямой к параметрическому виду:

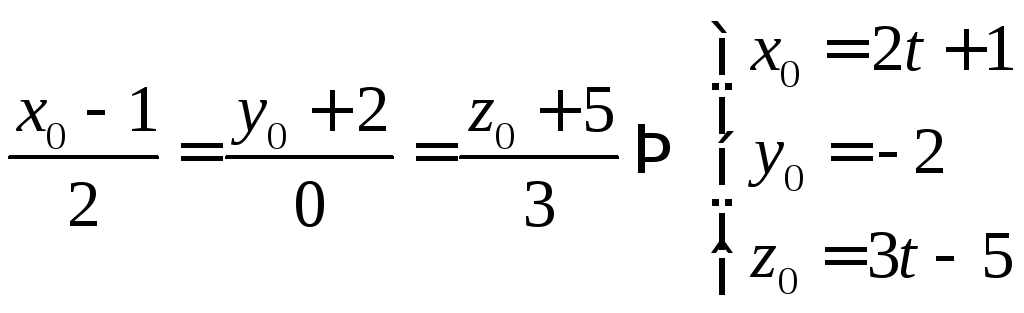
И затем решим ее методом подстановки.

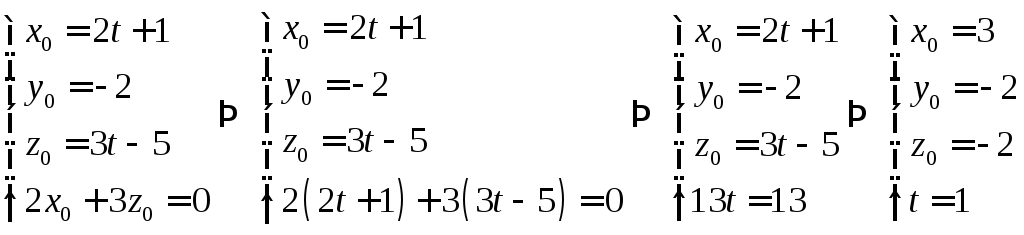
Таким образом .