- •Предварительные сведения
- •I. Символы и обозначения
- •III. Основные алгебраические соотношения
- •IV. Основные тригонометрические соотношения рис
- •Раздел 1. Линейная алгебра
- •§1. Матрицы
- •1.1. Основные понятия. Сложение, вычитание, произведение матрицы на число, произведение матриц
- •1.3. Определитель. Действия над квадратными матрицами
- •1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1.
- •§ 2. Системы линейных алгебраических уравнений
- •2.1. Основные понятия
- •2.2. Методы решения слау
- •Раздел 2. Векторная алгебра
- •§ 1. Векторы. Основные понятия
- •1.1. Геометрические векторы. Линейные операции
- •1.2. Проекция вектора на ось
- •§2. Координатное представление вектора
- •2.1. Разложение вектора по декартову базису. Координаты вектора
- •2.2. Скалярное произведение векторов
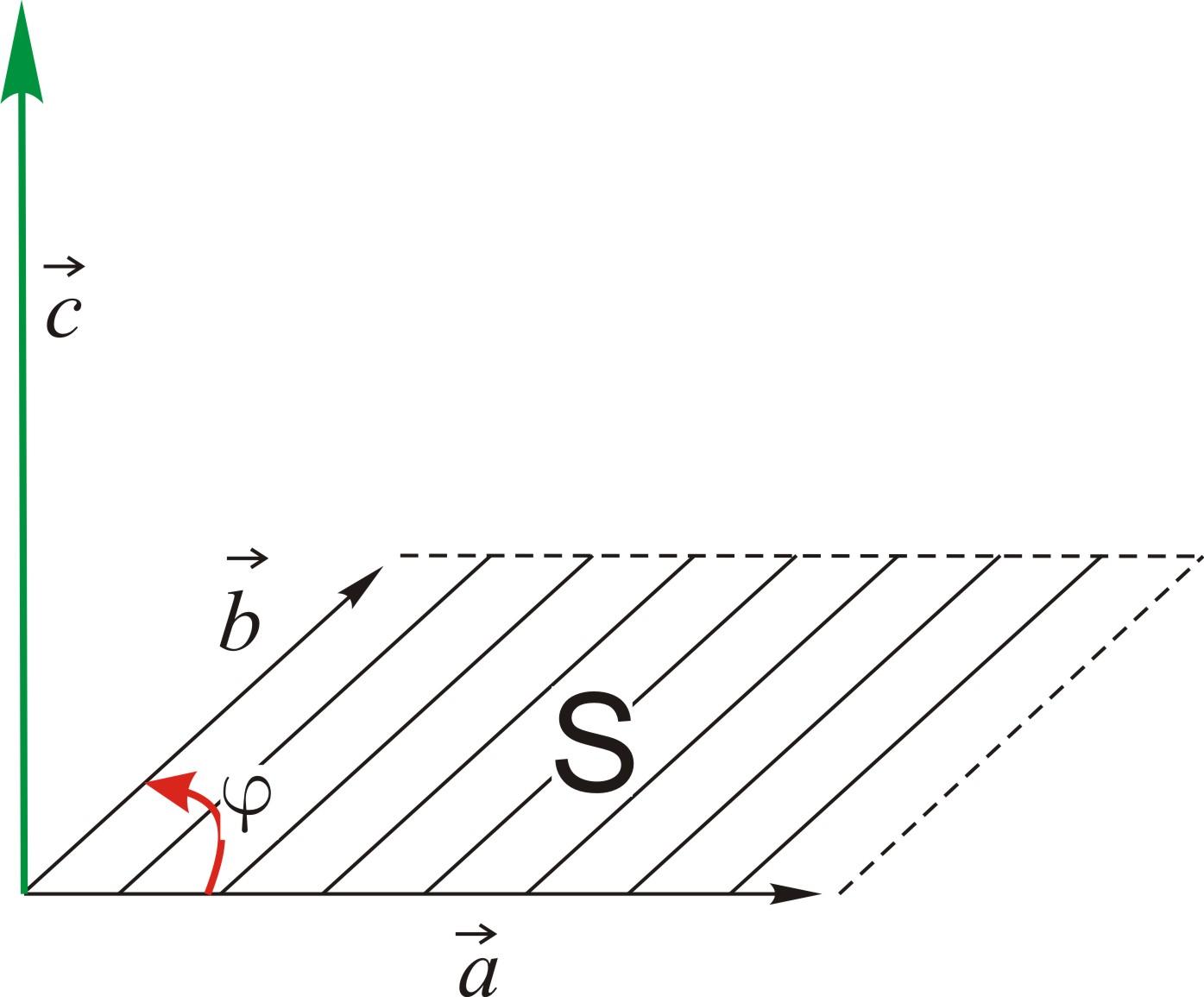
- •2.3. Векторное произведение векторов
- •2.4. Смешанное произведение векторов
- •2.5. Пространство .
- •Раздел 3. Аналитическая геометрия Уравнение линии на плоскости
- •Угловой коэффициент прямой на плоскости. Уравнение прямой с угловым коэффициентом
- •Практические приемы отыскания уравнения прямой
- •Кривые второго порядка
- •Уравнение поверхности и линии в пространстве
- •Поверхности второго порядка
2.2. Скалярное произведение векторов
р ис
Скалярным произведением
вектора
ис
Скалярным произведением
вектора
![]() на вектор
на вектор![]() называетсячисло
называетсячисло
![]() ,
,
где
![]() .
.
Например,
![]()
Свойства скалярного произведения.
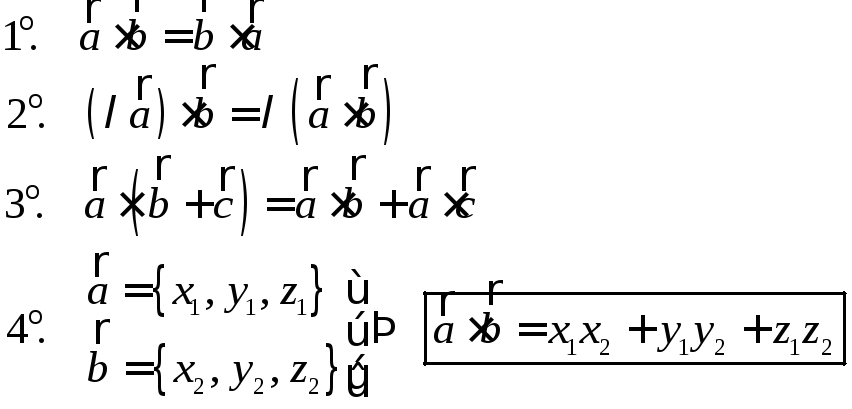
Приложения скалярного произведения
1.
![]() .
.
2.
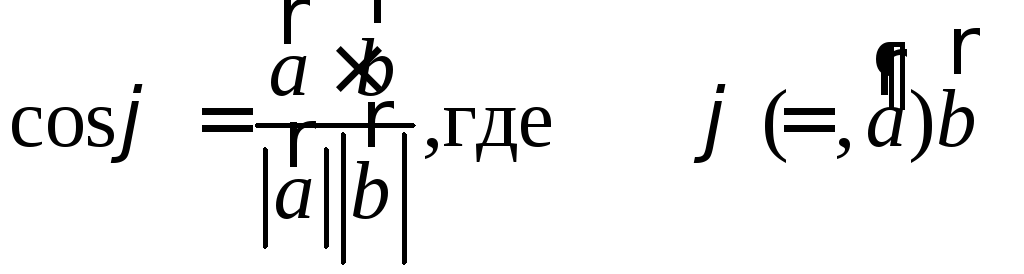 .
.
2а.
![]() .
.
3.
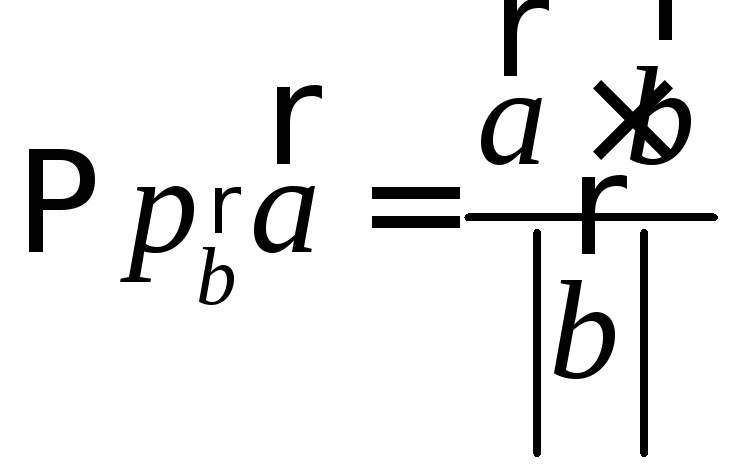
4. Работа постоянной
силы
![]() при
перемещении вдоль
вектора
при
перемещении вдоль
вектора
![]() равна
равна![]() .
.
Пример 2.3. Найти
угол между векторами
![]() и
и
![]() .
.
Решение.
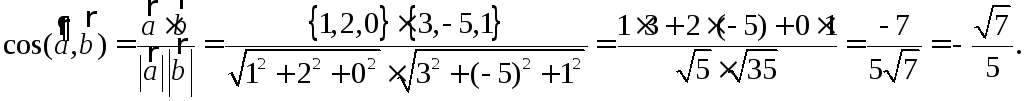
Ответ:
![]()
2.3. Векторное произведение векторов
Т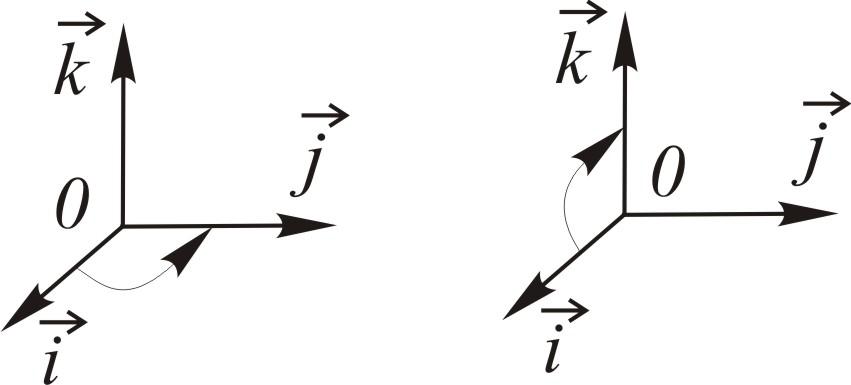 ройка
некомпланарных (не лежащих в одной
плоскости) векторов
ройка
некомпланарных (не лежащих в одной
плоскости) векторов![]() в указанном порядке образуетправую
тройку, если
с конца третьего вектора
в указанном порядке образуетправую
тройку, если
с конца третьего вектора
![]() кратчайший поворот от первого вектора
кратчайший поворот от первого вектора![]() ко второму вектору
ко второму вектору![]() наблюдается против часовой стрелки. В
противном случае тройка называетсялевой.
наблюдается против часовой стрелки. В
противном случае тройка называетсялевой.
Например,
![]() – правая тройка,
– правая тройка,![]() – левая.
– левая.
 Рис
Векторным произведением
Рис
Векторным произведением
![]() вектора
вектора![]() на вектор
на вектор![]() называетсявектор
называетсявектор
![]() такой, что
такой, что
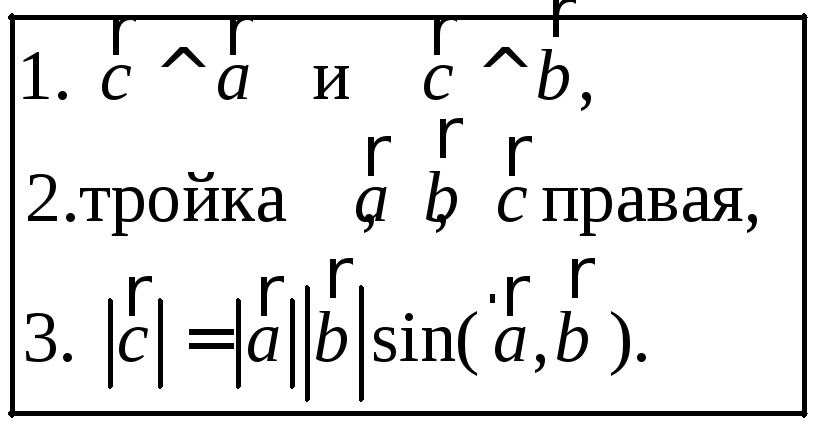
Свойства векторного произведения.
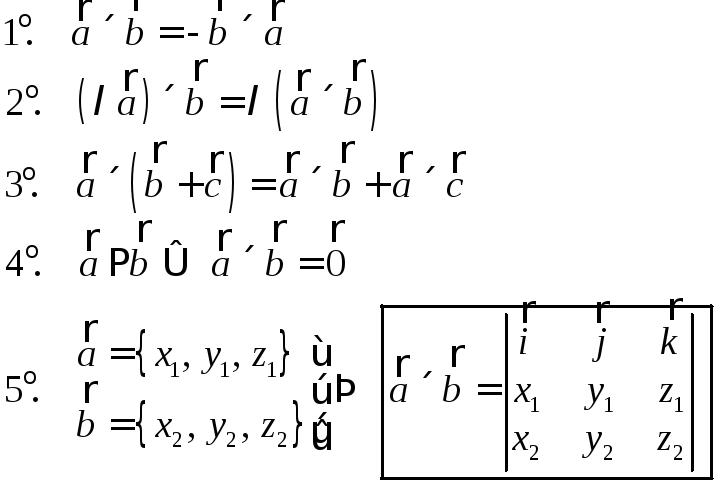
Приложения векторного произведения
|
1.
Площадь параллелограмма, построенного
на векторах
|
|
|
2.
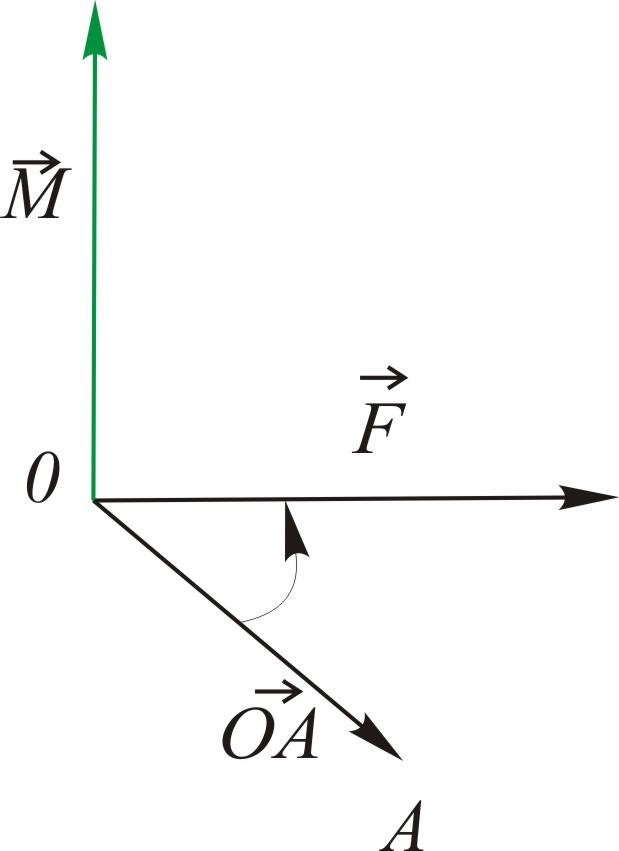
Момент силы
|
|
Пример 2.3. Найти
векторное произведение векторов
![]() ,
если известны координаты точек
,
если известны координаты точек![]() .
.
Решение. Сначала найдем координаты векторов по правилу «конец минус начало»:
![]() .
Далее возможны два способа решения.
.
Далее возможны два способа решения.
I
способ. Запишем векторы в виде
![]() и, с учетом свойств
и, с учетом свойств![]() получим:
получим:
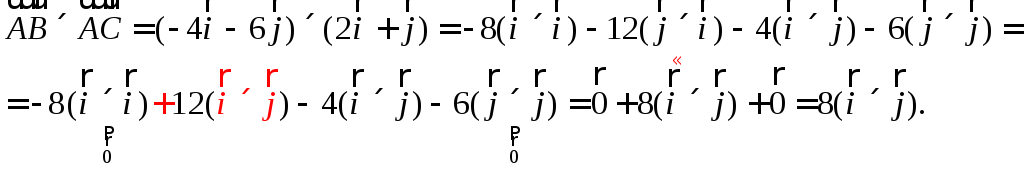
Всем пунктам
определения векторного произведения
![]() отвечает вектор
отвечает вектор![]() ,
таким образом
,
таким образом![]() .
.
II
способ. Векторы
![]() заданы в базисе
заданы в базисе![]() .
Если ввести третью координату (например,
0), то можно найти их векторное произведение,
пользуясь свойством
.
Если ввести третью координату (например,
0), то можно найти их векторное произведение,
пользуясь свойством![]() :
:
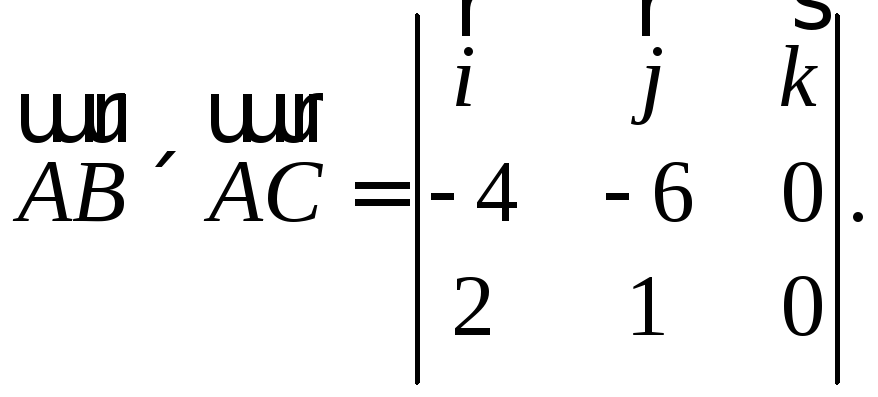
Определитель в правой части
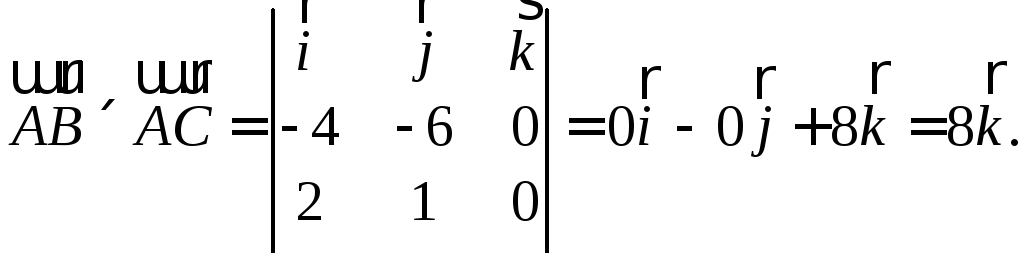
Ответ:
![]()
2.4. Смешанное произведение векторов
Смешанным
произведением
векторов
![]() называетсячисло
называетсячисло
![]() .
.
Свойства вытекают из свойств скалярного и векторного произведений. В частности
 .
.
П риложения
смешанного произведениярис
риложения
смешанного произведениярис
1. Объем параллелепипеда,
построенного на векторах
![]() ,
равен
,
равен![]() .
.
1а. Векторы
![]() компланарны
компланарны![]() .
.
2. Тройка
![]() правая
правая![]() ;
тройка
;
тройка![]() левая
левая![]() .
.
Пример
2.4. Выяснить, лежат ли векторы![]() в одной плоскости. Найти
смешанное произведение векторов
в одной плоскости. Найти
смешанное произведение векторов
![]() ,
если
,
если
Решение.
I
способ. Воспользуемся результатом
примера 2.3 и вычислим смешанное
произведение по определению:
![]()
найденным ранее (см.) произведением
II
способ. С учетом правила «конец
минус начало»,
замечания… и свойства
![]() ,
получим:
,
получим:
2.5. Пространство .
Последовательность
![]() из
из
![]() действительных чисел, расположенных в
определенном порядке, называется
действительных чисел, расположенных в
определенном порядке, называется![]() -мерным
вектором.
Совокупность всех
-мерным
вектором.
Совокупность всех
![]() -мерных
векторов
-мерных
векторов
![]() (
(![]() )
обозначим
)
обозначим![]() . Введем в
. Введем в![]() операции сложения и умножения на
вещественное число поэлементно:
операции сложения и умножения на
вещественное число поэлементно:
![]() ,
,
нуль-вектором
назовем вектор, все координаты которого
равны нулю:
![]() .
.
Множество, на
котором введены операции сложения и
умножения на число, удовлетворяющие
обычным свойствам арифметических
действий, называется линейным
пространством.
Таким образом, множество
![]() с введенными выше операциями является
линейным пространством.
с введенными выше операциями является
линейным пространством.
Совокупность из
![]() векторов пространства
векторов пространства![]() будем называтьлинейно
независимой,
если их линейная комбинация
будем называтьлинейно
независимой,
если их линейная комбинация
![]() (*)
(*)
лишь при условии
![]() .В противном
случае, т.е. если существуют такие числа
.В противном
случае, т.е. если существуют такие числа
![]() не все
равные нулю, что выполняется равенство
(*), совокупность
не все
равные нулю, что выполняется равенство
(*), совокупность
![]() назовемлинейно
зависимой.
назовемлинейно
зависимой.
Так, например,
векторы
![]() в пространстве
в пространстве![]() являются линейно зависимыми, т.к.
существует их нетривиальная (не все
являются линейно зависимыми, т.к.
существует их нетривиальная (не все
![]() равны
нулю) линейная комбинация, равная
нуль-вектору:
равны
нулю) линейная комбинация, равная
нуль-вектору:
![]() .
.
Обозначим
![]() – вектор
из
– вектор
из
![]() ,
все координаты которого равны нулю, за
исключением
,
все координаты которого равны нулю, за
исключением![]() -
ой, которая равна
-
ой, которая равна![]() :
:
![]() .
.
Эта система
векторов линейно независима, и любой
вектор
![]() единственным
образом
можно представить в виде линейной
комбинации этих векторов:
единственным
образом
можно представить в виде линейной
комбинации этих векторов:
![]() .
.
Любая система
![]() векторов, обладающих такими свойствами,
называетсябазисом
пространства
векторов, обладающих такими свойствами,
называетсябазисом
пространства
![]() .
.
В случаях
![]() вектор
вектор![]() можно рассматривать как вектор, заданный
своими проекциями на оси координат.
Тогда в «привычных» обозначениях:
система
можно рассматривать как вектор, заданный
своими проекциями на оси координат.
Тогда в «привычных» обозначениях:
система![]() является базисом в пространстве
является базисом в пространстве![]() ,
а
,
а![]() – в
– в![]() .
.
В
![]() существует бесконечное множество
базисов. В частности, в
существует бесконечное множество
базисов. В частности, в![]() –
это любая пара неколлинеарных, а в
–
это любая пара неколлинеарных, а в![]() –
любая тройка некомпланарных векторов.
–
любая тройка некомпланарных векторов.
![]() Покажем, что
векторы
Покажем, что
векторы
![]() образуют базис в
образуют базис в![]() ,
и найдем разложение вектора
,
и найдем разложение вектора![]() по базису
по базису![]()
1. Составим
линейную комбинацию
![]() .
Выясним условия на
.
Выясним условия на![]() ,
при которых эта комбинация дает
,
при которых эта комбинация дает![]() .
.
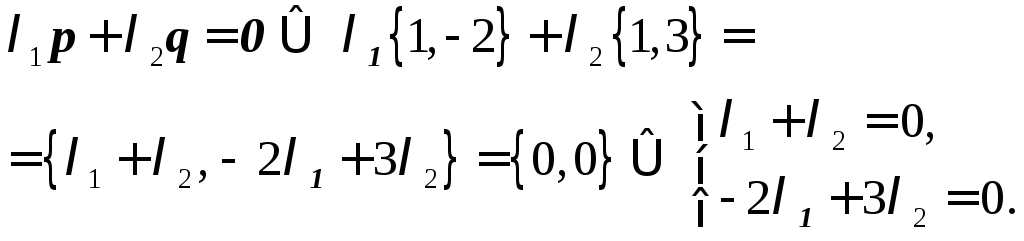

Определитель
полученной однородной системы
![]() ,
значит (см.
замечание к теме «СЛАУ»)
она имеет только тривиальное решение
,
значит (см.
замечание к теме «СЛАУ»)
она имеет только тривиальное решение
![]() .
.
2. Найдем координаты
вектора в этом базисе:
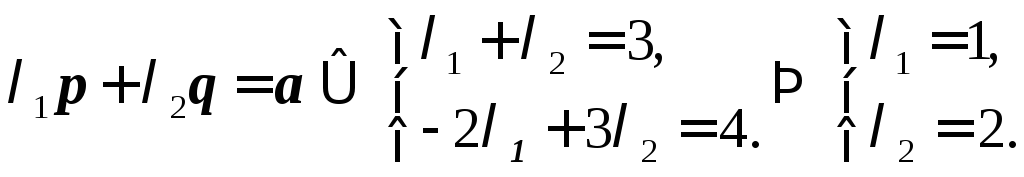 .
.
Ответ:
![]() .
(На рис результат проиллюстрирован
геометрически.)
.
(На рис результат проиллюстрирован
геометрически.)