
- •Предварительные сведения
- •I. Символы и обозначения
- •III. Основные алгебраические соотношения
- •IV. Основные тригонометрические соотношения рис
- •Раздел 1. Линейная алгебра
- •§1. Матрицы
- •1.1. Основные понятия. Сложение, вычитание, произведение матрицы на число, произведение матриц
- •1.3. Определитель. Действия над квадратными матрицами
- •1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1.
- •§ 2. Системы линейных алгебраических уравнений
- •2.1. Основные понятия
- •2.2. Методы решения слау
- •Раздел 2. Векторная алгебра
- •§ 1. Векторы. Основные понятия
- •1.1. Геометрические векторы. Линейные операции
- •1.2. Проекция вектора на ось
- •§2. Координатное представление вектора
- •2.1. Разложение вектора по декартову базису. Координаты вектора
- •2.2. Скалярное произведение векторов
- •2.3. Векторное произведение векторов
- •2.4. Смешанное произведение векторов
- •2.5. Пространство .
- •Раздел 3. Аналитическая геометрия Уравнение линии на плоскости
- •Угловой коэффициент прямой на плоскости. Уравнение прямой с угловым коэффициентом
- •Практические приемы отыскания уравнения прямой
- •Кривые второго порядка
- •Уравнение поверхности и линии в пространстве
- •Поверхности второго порядка
§ 2. Системы линейных алгебраических уравнений
2.1. Основные понятия
Системой линейных алгебраических уравнений (СЛАУ) называется система вида
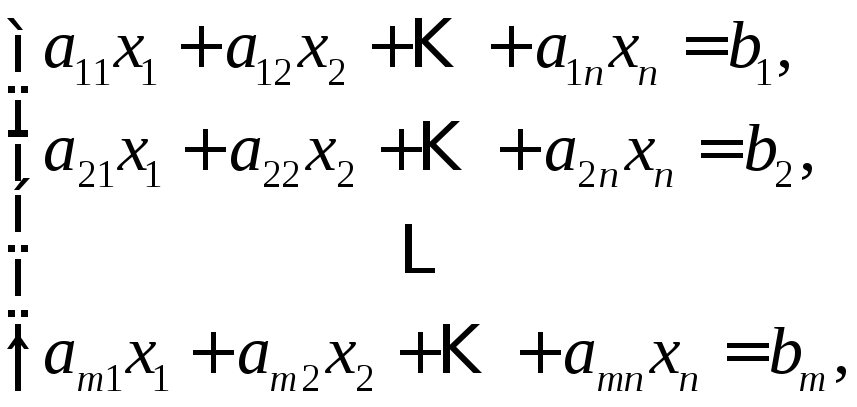 (1.4)
(1.4)
где числа
![]() – коэффициенты системы,
– коэффициенты системы,![]() – свободные члены,
– свободные члены,![]() –
неизвестные (подлежат нахождению).
–
неизвестные (подлежат нахождению).
Решением
системы
(1.4) называется
![]() значений неизвестных
значений неизвестных![]() ,
при подстановке которых все уравнения
системы обращаются в верные равенства.
,
при подстановке которых все уравнения
системы обращаются в верные равенства.
Известно, что СЛАУ может
-не иметь решений (система называется несовместной);
-иметь единственное решение (система называется определенной);
-иметь бесконечное множество решений (система называется неопределенной).
Решить систему – значит найти все ее решения или доказать, что она несовместна.
Систему (4) можно записать в виде
![]() .
.
Здесь
![]() -основная
матрица
системы,
-основная
матрица
системы,
 –столбец
неизвестных,
–столбец
неизвестных,
 –
столбец свободных членов.
–
столбец свободных членов.
Приведем некоторые метода решения СЛАУ.
Эквивалентные СЛАУ
Напомним следующее свойство СЛАУ. Если
- переставить местами уравнения,
- умножить любое уравнение системы на ненулевое число,
- заменить какое-либо уравнение суммой этого уравнения с другим уравнением системы,
- внести в систему или вычеркнуть из системы уравнение, представляющее собой тождество,
- вычеркнуть из системы одно из пропорциональных уравнений,
то полученная после одного или нескольких таких преобразований система будет иметь то же решение, что и исходная или являться несовместной, как и исходная.
Системы, множество решений которых совпадает, называются эквивалентными.
2.2. Методы решения слау
Матричный метод
Рассмотрим
квадратную (число уравнений равно числу
неизвестных), невырожденную (![]() )
СЛАУ
)
СЛАУ![]() .
При указанных условиях существует
матрица, обратная к
.
При указанных условиях существует
матрица, обратная к![]() .
Чтобы найти неизвестную
.
Чтобы найти неизвестную![]() ,
умножим обе части слева на
,
умножим обе части слева на![]() .
Тогда
.
Тогда

Отсюда получим
формулу для отыскания
![]() :
:
![]()
Пример 1.7.
Решить СЛАУ

Решение. Обозначим
 .
.
Для отыскания
![]() можно применить полученную выше формулу,
т.к. основная матрица системы
можно применить полученную выше формулу,
т.к. основная матрица системы![]() – квадратная, и ее определитель –основной
определитель
–
– квадратная, и ее определитель –основной
определитель
–
![]() (см. пример 1.6). Таким образом
(см. пример 1.6). Таким образом

(матрица
![]() была найдена в примере 1.6).
была найдена в примере 1.6).
Ответ:
![]() .
.
Убедимся в
правильности результата – подставим
![]() в каждое уравнение системы:
в каждое уравнение системы:
![]() .
.
Все уравнения обратились в тождества, что и требовалось доказать.
Замечание. Ответ
к задаче можно дать в другом виде:
 или просто
или просто![]()
Формулы Крамера
Из системы
![]() найдем
в общем виде, например,
найдем
в общем виде, например,![]() .
Здесь
.
Здесь
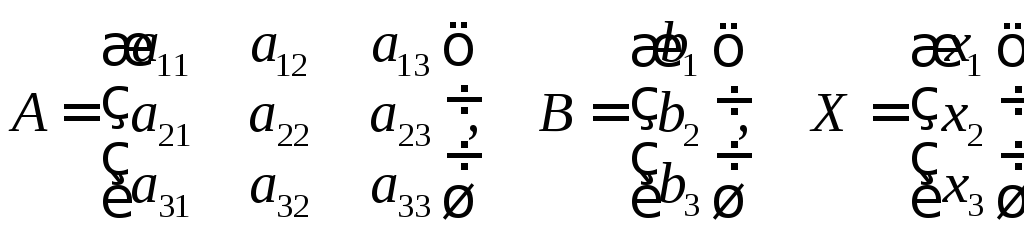 .
.
 ,
,
![]() .
.
Это равенство
можно записать в виде
![]() ,
где обозначено
,
где обозначено
 .
.
Вообще, при
![]() ,
для решений СЛАУ справедливыформулы
Крамера:
,
для решений СЛАУ справедливыформулы
Крамера:
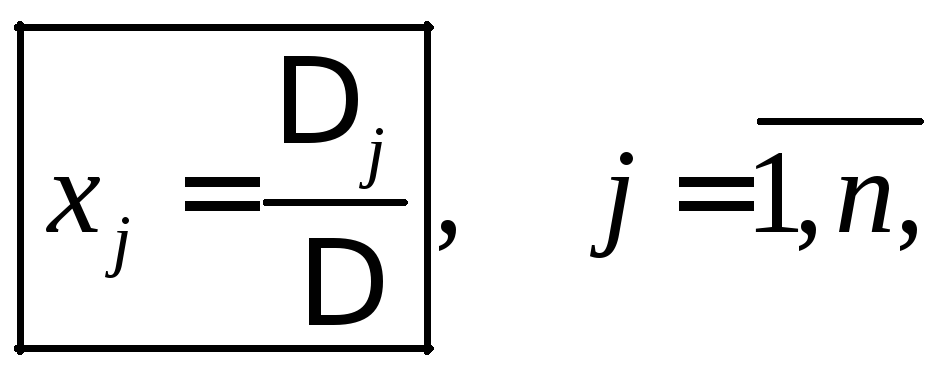
где
![]() – определитель основной матрицы системы,
– определитель основной матрицы системы,![]() получается из
получается из![]() заменой
заменой![]() -го
столбца столбцом свободных членов.
-го
столбца столбцом свободных членов.
Например, систему
 можно решить по формулам Крамера, т.к.
это система двух линейных уравнений с
двумя неизвестными, и
можно решить по формулам Крамера, т.к.
это система двух линейных уравнений с
двумя неизвестными, и![]() .
.
Вычислим
вспомогательные определители![]() .
.
Отсюда
![]() .
.
Ответ:
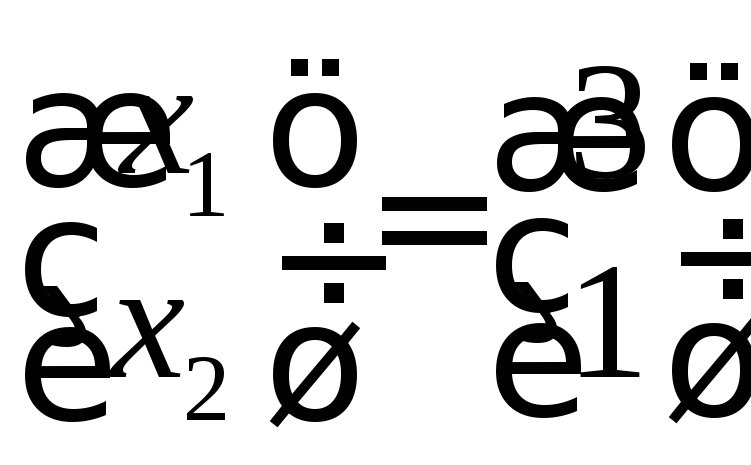 .
.
Метод подстановки
Проиллюстрируем этот метод на простом примере «треугольной» системы.
Пример 1.8. Решить
СЛАУ методом подстановки

Решение. Из
третьего уравнения найдем неизвестную
![]() и подставим ее значение во второе
уравнение, откуда вычислим
и подставим ее значение во второе
уравнение, откуда вычислим![]() :
:
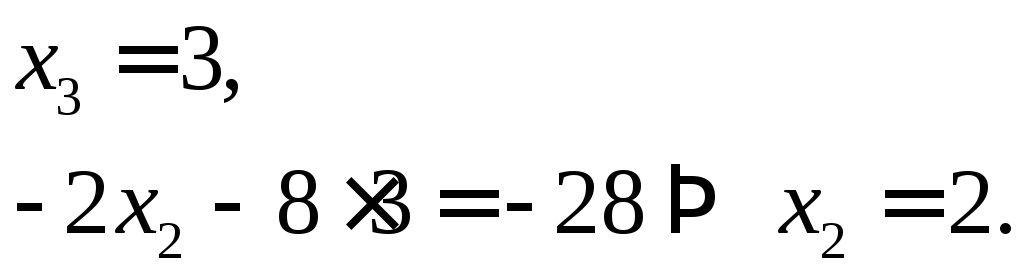 .
.
Далее подставим
значения
![]() и
и![]() в первое уравнение, откуда найдем
в первое уравнение, откуда найдем![]() :
:
![]() .
.
Ответ:
![]() .
.
Метод Гаусса
Рассмотрим систему (1.4)
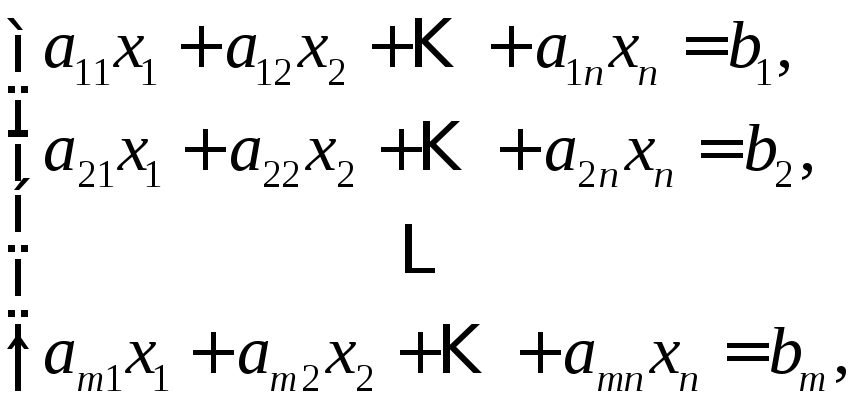 ,
,
где
![]() ,
,![]() не обязательно равно
не обязательно равно![]() ,
а в случае
,
а в случае![]() не обязательно отличен от нуля.
не обязательно отличен от нуля.
Суть метода Гаусса – последовательный переход от исходной системы к эквивалентной ей «треугольной » системе
 ,
,
которая без труда решатся методом подстановки .
Всю информацию о системе содержит так называемая расширенная матрица СЛАУ, она имеет вид:
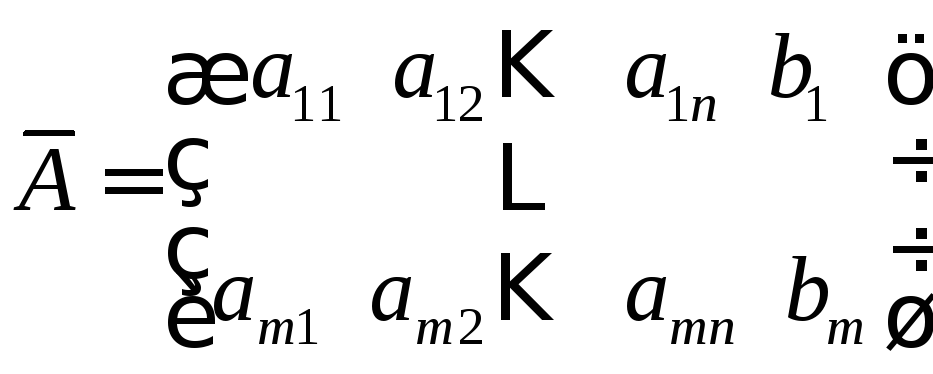 .
.
Будем выделять прямой и обратный ход метода Гаусса.
I. Прямой ход. Элементарными преобразованиями над строками приводим расширенную матрицу системы к «трапециевидной».
II. Обратный ход. По последней матрице восстанавливаем СЛАУ, которая, очевидно, эквивалентна исходной, и приводим ее к треугольному виду. Решаем ее методом подстановки «снизу вверх».
Пример 1.9. Решить СЛАУ методом Гаусса
1.9а.

Решение.
I.
Прямой ход.


II. Обратный ход.

Эта система была решена в (см. пример 1.8).
Ответ:
![]()
1.9б.

Решение.
I.
Прямой ход.

II. Обратный ход.

Третье и четвертое уравнения одинаковые, и мы вычеркнули одно из них:

Последнее уравнение не имеет решений, значит, и вся система не имеет решения.
Ответ: система несовместна.
1.9в.

Решение.
I. Прямой ход.
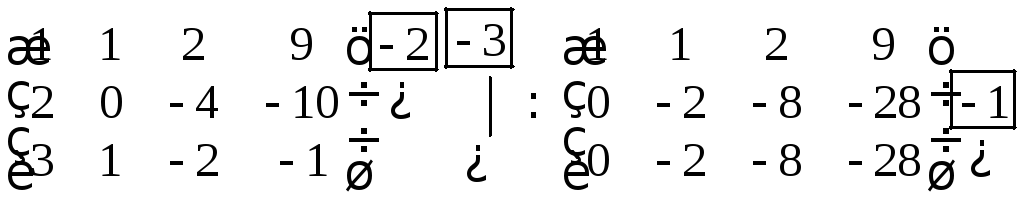

II. Обратный ход.

Последнему уравнению
удовлетворяет любое действительное
число, обозначим
![]() .
Выражая последовательно из второго
уравнения
.
Выражая последовательно из второго
уравнения![]() :
:
![]()
а затем из третьего
–
![]() :
:
![]() ,
,
получим бесконечное множество решений.
Ответ:
 .
.
1.9г.

Решение.
I. Прямой ход.

II. Обратный ход.

Чтобы привести
систему к треугольной, внесем в нее два
тождества
![]() :
:
|
|
|
Ответ:

Замечания:
-
Однородная система, т.е. система (1.4), где
![]() ,
всегда совместна. Она имеет как минимум
одно решение
,
всегда совместна. Она имеет как минимум
одно решение![]() ,
так называемоетривиальное
решение. В частности, при
,
так называемоетривиальное
решение. В частности, при
![]() и
и![]() – однородная СЛАУ имеет нетривиальные
решения.
– однородная СЛАУ имеет нетривиальные
решения.
- При решении однородных систем столбец свободных членов после элементарных преобразований не меняется, поэтому достаточно преобразовывать основную матрицу системы.


