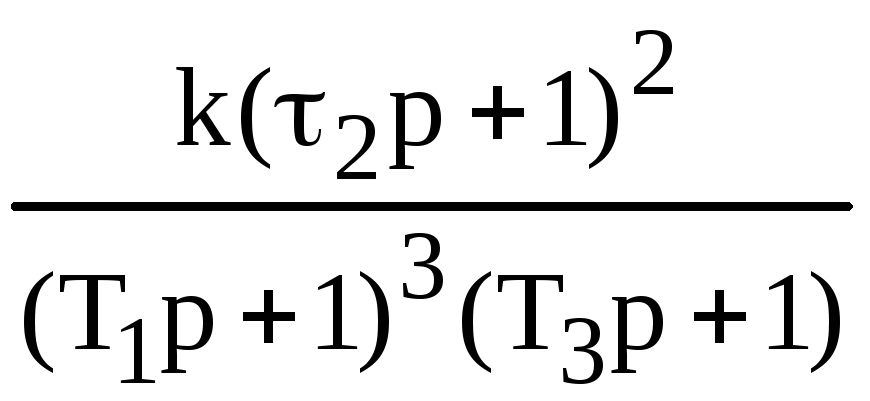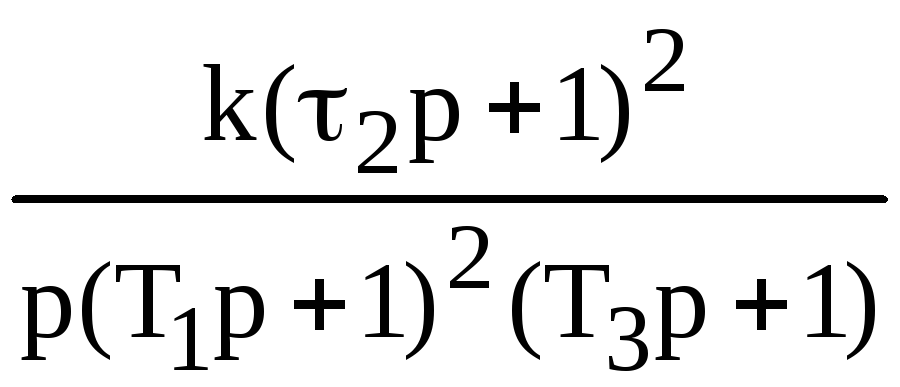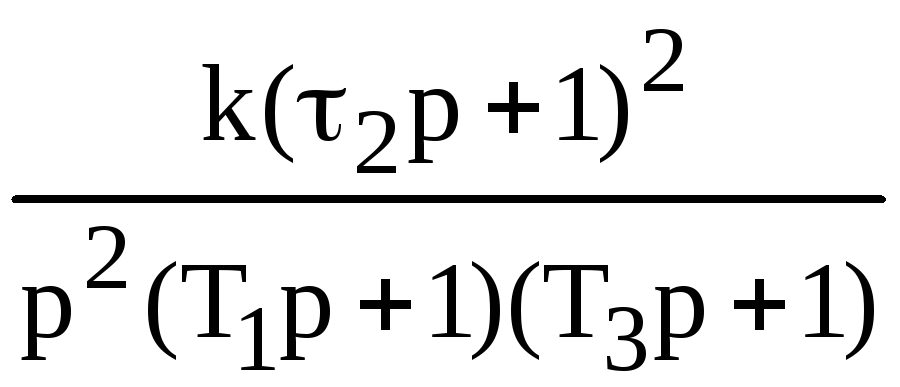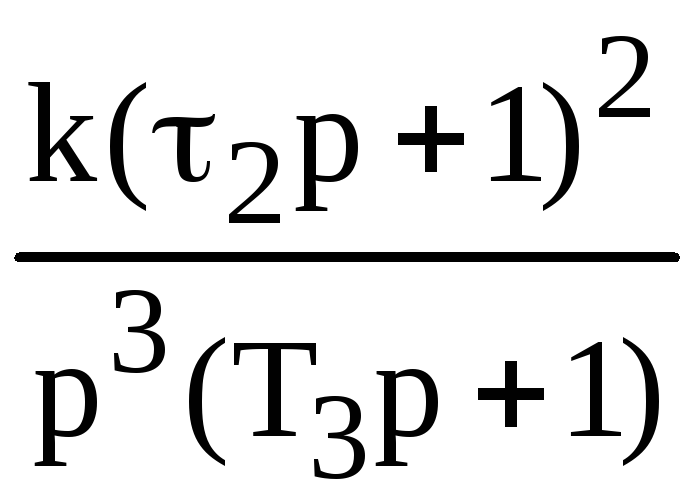- •В. Л. Федоров, а. В. Бубнов теория автоматического управления
- •Введение
- •1. Основные понятия теории автоматического управления
- •1.1. Классификация объектов управления
- •1.2. Принципы автоматического управления
- •1.2.1. Разомкнутые сау (принцип разомкнутого управления)
- •1.2.2. Принцип компенсации (управление по возмущению)
- •1.2.3. Принцип обратной связи. Регулирование по отклонению
- •1.2.4. Комбинированное управление (сочетание принципов замкнутой и разомкнутой систем)
- •1.3. Понятие о качестве систем автоматического управления
- •1.4. Классификация систем автоматического управления
- •1.4.5. Классификация по свойствам объекта управления и регулятора
- •1.4.6. Классификация по идеализации математического описания
- •1.4.7. Классификация по количеству регулируемых величин
- •1.4.8. Классификация по свойствам в установившемся режиме (величине ошибки регулирования)
- •1.5. Типовая функциональная схема сау
- •2. Линейные системы автоматического управления
- •2.1. Передаточные функции
- •2.2. Частотные характеристики
- •2.3. Логарифмические частотные характеристики
- •2.4. Типовые динамические звенья сау
- •2.4.1. Усилительное звено (идеальное усилительное, безынерционное, пропорциональное)
- •2.4.2. Апериодическое звено (инерционное, апериодическое первого порядка)
- •2.4.3. Интегрирующее звено
- •2.4.4. Дифференцирующее звено (идеальное дифференцирующее звено)
- •2.4.5. Форсирующее звено (форсирующее звено первого порядка)
- •2.4.6. Реальное дифференцирующее звено (не типовое звено)
- •2.4.7. Колебательное звено
- •2.4.8. Звено чистого запаздывания
- •2.5. Структурные схемы сау
- •2.5.1. Правила преобразования структурных схем
- •2.6. Передаточные функции замкнутой сау по задающему воздействию и возмущению
- •2.7. Построение логарифмических характеристик сау
- •2.8. Устойчивость линейных сау
- •2.8.1. Критерий устойчивости Гурвица
- •2.8.2. Критерий устойчивости Найквиста
- •2.8.3. Логарифмический критерий устойчивости
- •2.8.4. Запасы устойчивости по амплитуде и фазе
- •2.9. Точность сау в установившихся режимах
- •2.9.1. Точность сау в статическом стационарном режиме
- •2.9.1.2. Система управления с регулятором вида
- •2.9.2. Точность сау в динамическом стационарном режиме
- •2.9.3. Коэффициенты ошибок
- •2.9.4. Определение установившейся ошибки при движении сау по гармоническому закону
- •2.10. Повышение статической точности сау
- •2.10.1. Повышение коэффициента передачи k разомкнутой цепи
- •2.10.2. Повышение порядка астатизма сау
- •2.11. Синтез систем автоматического управления
- •2.11.1. Основные этапы синтеза сау.
- •2.11.2. Частотный синтез. Типовые лах
- •2.11.3. Выбор желаемой типовой лах
- •2.11.4. Связь параметров типовых лах между собой и с показателями качества переходного процесса
- •2.11.5. Определение передаточной функции корректирующего устройства
- •2.11.6. Пример синтеза сау
- •2.12. Корректирующие устройства сау
- •2.12.1. Виды корректирующих устройств
- •Библиографический список
- •Содержание
- •2. Линейные системы автоматического управления 24
2.11. Синтез систем автоматического управления
2.11.1. Основные этапы синтеза сау.
Процесс синтеза САУ состоит из трех этапов.
1. Исходя из требований к назначению системы и особенностей ее конструкции следует выбрать функционально необходимые элементы (ФНЭ) – объект управления, датчики сигналов, задающие устройства, элементы сравнения, усилители мощности, исполнительные элементы. При выборе ФНЭ учитываются мощность, необходимая для управления объектом, предельные значения скоростей и ускорений выходных величин ОУ, допустимые ошибки, требуемый порядок астатизма. В результате решения этой задачи основа структуры проектируемой САУ становится известной.
2. На основании сведений о задающих и возмущающих воздействиях, об ограничениях, накладываемых на ход процесса управления, требований к точности и быстродействию необходимо определить желаемые динамические характеристики САУ. Последние являются компромиссным решением между качеством и точностью, с одной стороны, и простотой технической реализации и надежностью, – с другой.
3. На последнем этапе необходимо выбрать (рассчитать) корректирующие устройства (КУ), которые приближают с заданной степенью точности характеристики системы, состоящей из функционально необходимых элементов, к характеристикам желаемой системы.
Существует большое количество методов синтеза систем управления. Это объясняется как разнообразием исходных данных и требований к САУ, так и сложностью задачи синтеза. Необходимо учитывать, что задача не имеет однозначного решения и нельзя ожидать высокой точности получаемых результатов.
Широкое распространение получили частотные методы синтеза. В этом случае желаемые динамические характеристики САУ представляются в виде логарифмических частотных характеристик. При построении желаемых ЛАХ (ЖЛАХ) удобно пользоваться так называемыми типовыми (стандартными) ЛАХ, параметры которых связаны с показателями качества и точностью системы.
2.11.2. Частотный синтез. Типовые лах
Если в САУ не входят колебательные и дифференцирующие звенья второго порядка, то типовым ЛАХ (рис. 2.90) в общем случае соответствует передаточная функция вида
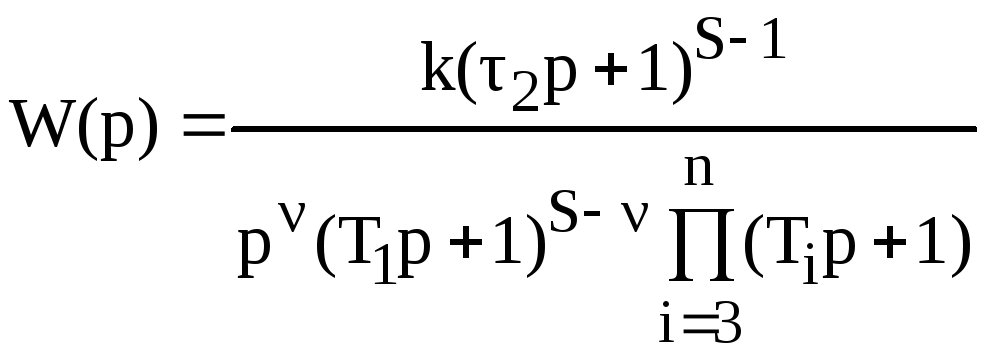 ,
(2.257)
,
(2.257)
где S = const.
В типовых ЛАХ выделяют четыре основных области..
1.
Область очень
низких частот
![]() .
Наклон ЛАХ на интервале
.
Наклон ЛАХ на интервале![]() определяется порядком астатизма САУ
определяется порядком астатизма САУ![]() (количеством интегрирующих звеньев).
(количеством интегрирующих звеньев).
2.
Область
низких частот
![]() .
Наклон ЛАХ определяется числом
апериодических звеньев с постоянной
времени
.
Наклон ЛАХ определяется числом
апериодических звеньев с постоянной
времени![]() .
.
Первые две области определяют в основном точность воспроизведения медленно меняющихся воздействий и статическую точность САУ.
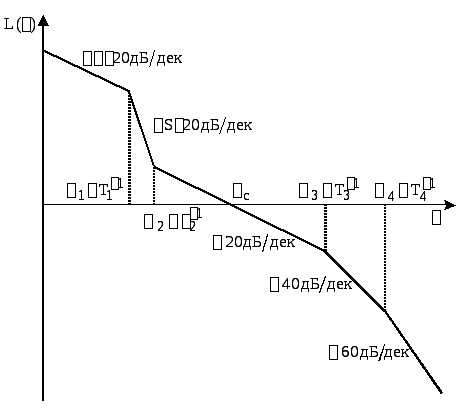
Рисунок 2.90
3.
Область
средних частот
![]() .
Наклон ЛАХ в этом интервале определяет
запасы устойчивости по амплитуде и фазе
и в значительной мере качество системы
в переходном режиме. Для обеспечения
приемлемых запасов устойчивости наклон
ЛАХ принимается равным (
.
Наклон ЛАХ в этом интервале определяет
запасы устойчивости по амплитуде и фазе
и в значительной мере качество системы
в переходном режиме. Для обеспечения
приемлемых запасов устойчивости наклон
ЛАХ принимается равным (![]() ).
).
Протяженность
среднечастотного участка ЛАХ влияет
на колебательность САУ. Так, если его
ширина примерно равна одной декаде, то
перерегулирование
![]() (20
– 30)%.
(20
– 30)%.
В
области средних частот располагается
частота среза
![]() .
Чем больше
.
Чем больше![]() ,
тем меньше время регулирования
,
тем меньше время регулирования![]() .
.
4.
Область
высоких частот
![]() .
Наклон ЛАХ в этой области определяется
количеством апериодических звеньев с
постоянными времени
.
Наклон ЛАХ в этой области определяется
количеством апериодических звеньев с
постоянными времени![]() (формула (2.249)). Высокочастотная часть
незначительно влияет на динамические
свойства системы управления. Ее наклон
желательно выбирать как можно большим,
что уменьшает требуемую мощность
исполнительных элементов и влияние
высокочастотных помех.
(формула (2.249)). Высокочастотная часть
незначительно влияет на динамические
свойства системы управления. Ее наклон
желательно выбирать как можно большим,
что уменьшает требуемую мощность
исполнительных элементов и влияние
высокочастотных помех.
Классификация
типовых ЛАХ осуществляется по величинам
порядка астатизма
![]() и коэффициентаS,
определяющим наклоны участков ЛАХ.
Обозначение типовой характеристики
имеет вид: ЛАХ –
и коэффициентаS,
определяющим наклоны участков ЛАХ.
Обозначение типовой характеристики
имеет вид: ЛАХ –
![]() .
Возможные сочетанияS
и
.
Возможные сочетанияS
и
![]() и соответствующие им передаточные
функции приведены в таблице 2.
и соответствующие им передаточные
функции приведены в таблице 2.
Таблица 2
|
|
1/0 |
1/1 |
2/0 |
|
|
|
|
|
|
|
2/1 |
2/2 |
3/0 |
|
|
|
|
|
|
|
3/1 |
3/2 |
3/3 |
|
|
|
|
|
С
целью упрощения записи передаточных
функций (табл. 2) опущены малоинерционные
звенья, постоянные времени которых
![]() .
.
Графики некоторых типовых ЛАХ приведены на рисунках 2.91–2.93.
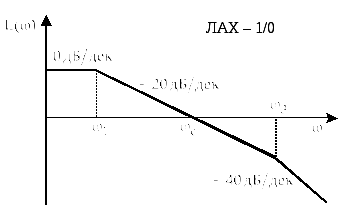
Рисунок 2.91
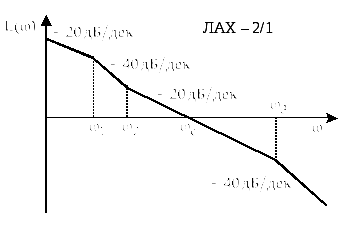
Рисунок 2.92
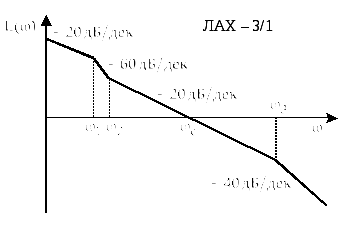
Рисунок 2.93