
- •В. Л. Федоров, а. В. Бубнов теория автоматического управления
- •Введение
- •1. Основные понятия теории автоматического управления
- •1.1. Классификация объектов управления
- •1.2. Принципы автоматического управления
- •1.2.1. Разомкнутые сау (принцип разомкнутого управления)
- •1.2.2. Принцип компенсации (управление по возмущению)
- •1.2.3. Принцип обратной связи. Регулирование по отклонению
- •1.2.4. Комбинированное управление (сочетание принципов замкнутой и разомкнутой систем)
- •1.3. Понятие о качестве систем автоматического управления
- •1.4. Классификация систем автоматического управления
- •1.4.5. Классификация по свойствам объекта управления и регулятора
- •1.4.6. Классификация по идеализации математического описания
- •1.4.7. Классификация по количеству регулируемых величин
- •1.4.8. Классификация по свойствам в установившемся режиме (величине ошибки регулирования)
- •1.5. Типовая функциональная схема сау
- •2. Линейные системы автоматического управления
- •2.1. Передаточные функции
- •2.2. Частотные характеристики
- •2.3. Логарифмические частотные характеристики
- •2.4. Типовые динамические звенья сау
- •2.4.1. Усилительное звено (идеальное усилительное, безынерционное, пропорциональное)
- •2.4.2. Апериодическое звено (инерционное, апериодическое первого порядка)
- •2.4.3. Интегрирующее звено
- •2.4.4. Дифференцирующее звено (идеальное дифференцирующее звено)
- •2.4.5. Форсирующее звено (форсирующее звено первого порядка)
- •2.4.6. Реальное дифференцирующее звено (не типовое звено)
- •2.4.7. Колебательное звено
- •2.4.8. Звено чистого запаздывания
- •2.5. Структурные схемы сау
- •2.5.1. Правила преобразования структурных схем
- •2.6. Передаточные функции замкнутой сау по задающему воздействию и возмущению
- •2.7. Построение логарифмических характеристик сау
- •2.8. Устойчивость линейных сау
- •2.8.1. Критерий устойчивости Гурвица
- •2.8.2. Критерий устойчивости Найквиста
- •2.8.3. Логарифмический критерий устойчивости
- •2.8.4. Запасы устойчивости по амплитуде и фазе
- •2.9. Точность сау в установившихся режимах
- •2.9.1. Точность сау в статическом стационарном режиме
- •2.9.1.2. Система управления с регулятором вида
- •2.9.2. Точность сау в динамическом стационарном режиме
- •2.9.3. Коэффициенты ошибок
- •2.9.4. Определение установившейся ошибки при движении сау по гармоническому закону
- •2.10. Повышение статической точности сау
- •2.10.1. Повышение коэффициента передачи k разомкнутой цепи
- •2.10.2. Повышение порядка астатизма сау
- •2.11. Синтез систем автоматического управления
- •2.11.1. Основные этапы синтеза сау.
- •2.11.2. Частотный синтез. Типовые лах
- •2.11.3. Выбор желаемой типовой лах
- •2.11.4. Связь параметров типовых лах между собой и с показателями качества переходного процесса
- •2.11.5. Определение передаточной функции корректирующего устройства
- •2.11.6. Пример синтеза сау
- •2.12. Корректирующие устройства сау
- •2.12.1. Виды корректирующих устройств
- •Библиографический список
- •Содержание
- •2. Линейные системы автоматического управления 24
2.9.3. Коэффициенты ошибок
Если
функция
![]() дифференцируема и после окончания
переходного процесса существенное
значение имеет только конечное числоi
ее производных, то установившуюся ошибку
можно определить следующим образом.
дифференцируема и после окончания
переходного процесса существенное
значение имеет только конечное числоi
ее производных, то установившуюся ошибку
можно определить следующим образом.
Положим
для простоты, что возмущающее воздействие
отсутствует
![]() .
В соответствии с выражением (2.126) запишем
изображение ошибки:
.
В соответствии с выражением (2.126) запишем
изображение ошибки:
![]() .
(2.218)
.
(2.218)
Разложим
передаточную функцию замкнутой системы
относительно ошибки по задающему
воздействию
![]() в ряд Тэйлора, тогда выражение (2.218)
принимает вид
в ряд Тэйлора, тогда выражение (2.218)
принимает вид
![]() ,
(2.219)
,
(2.219)
где
![]() ,
,![]() ,
…,
,
…,![]() – коэффициенты ошибок.
– коэффициенты ошибок.
Переходя от изображения ошибки (2.219) к оригиналу, получим
![]() .
(2.220)
.
(2.220)
Коэффициенты ошибок можно определить следующими способами.
I. Воспользоваться известными формулами:
 ;
(2.221)
;
(2.221)
 ;
(2.222)
;
(2.222)
 ;
(2.223)
;
(2.223)
……………………..;
 .
(2.224)
.
(2.224)
Рассмотрим в качестве примера простейшую САУ, структурная схема которой приведена на рисунке 2.83.

Рисунок 2.83
Передаточная функция прямой цепи рассматриваемой системы
![]() .
(2.225)
.
(2.225)
Тогда передаточная функция замкнутой системы относительно ошибки по задающему воздействию имеет вид
![]() .
(2.226)
.
(2.226)
Определим
коэффициенты
![]() ,
,![]() ,
,![]() .
Согласно выражению (2.221), величина
.
Согласно выражению (2.221), величина![]() будет
будет
 .
(2.227)
.
(2.227)
Для
расчета коэффициента
![]() возьмем первую производную от передаточной
функции (2.226):
возьмем первую производную от передаточной
функции (2.226):
![]() .
(2.228)
.
(2.228)
В
соответствии с формулой (2.213) коэффициент
![]() будет
будет
![]() .
(2.229)
.
(2.229)
Для
определения коэффициента
![]() возьмем вторую производную от передаточной
функции (2.226):
возьмем вторую производную от передаточной
функции (2.226):
 .
(2.230)
.
(2.230)
Тогда
на основании формулы (2.223) коэффициент
![]() будет
будет
![]() .
(2.231)
.
(2.231)
II.
Если
![]() является дробно-рациональной функцией
вида (2.3), то ее разложение в ряд Тэйлора
с последующим выделением коэффициентов
ошибок можно осуществить простым
делением полинома числителя на полином
знаменателя, располагая члены полиномов
в порядке возрастания степеней.
является дробно-рациональной функцией
вида (2.3), то ее разложение в ряд Тэйлора
с последующим выделением коэффициентов
ошибок можно осуществить простым
делением полинома числителя на полином
знаменателя, располагая члены полиномов
в порядке возрастания степеней.
Разделим полином числителя (2.226) на полином знаменателя:
![]() (2.232)
(2.232)
Сравнивая (2.232) и (2.219), получим
![]() ,
(2.233)
,
(2.233)
![]() ,
(2.234)
,
(2.234)
![]() .
(2.235)
.
(2.235)
Из формулы (2.235) следует
![]() .
(2.236)
.
(2.236)
Покажем,
как можно определить
![]() с помощью коэффициентов ошибок на
примере САУ (см. рис. 2.83).
с помощью коэффициентов ошибок на
примере САУ (см. рис. 2.83).
Пусть на вход системы подается задающее воздействие вида
![]() .
(2.237)
.
(2.237)
В соответствии с формулой (2.220) необходимо взять первую производную от задающего воздействия (2.237)
![]() .
(2.238)
.
(2.238)
Тогда, согласно формуле (2.220), величина установившейся ошибки
![]() ,
(2.239)
,
(2.239)
или
![]() .
(2.240)
.
(2.240)
Учитывая выражения (2.233) и (2.234), окончательно получим
![]() .
(2.241)
.
(2.241)
Полученный
результат подтверждает вывод, сделанный
в пп. 2.9.2: если
степень временной функции задающего
воздействия
m
(в рассмотренном
примере m
= 1) больше
порядка астатизма системы
![]() (
(![]() ),
то с течением времени ошибка неограниченно
возрастает:
),
то с течением времени ошибка неограниченно
возрастает:
![]() .
.
Так,
на рисунке 2.84 приведены графики изменения
во времени задающего воздействия
(2.237), выходной величины
![]() и ошибки регулирования
и ошибки регулирования![]() в системе (см. рис. 2.83).
в системе (см. рис. 2.83).

Рисунок 2.84
Данное
обстоятельство (неограниченный рост
ошибки при
![]() )
необходимо учитывать при проектировании
систем управления соответствующим
выбором порядка астатизма САУ.
)
необходимо учитывать при проектировании
систем управления соответствующим
выбором порядка астатизма САУ.
Отметим,
что результат вычисления установившейся
ошибки
![]() с помощью формулы (2.220) справедлив только
после окончания переходного процесса
в системе (рис. 2.85).
с помощью формулы (2.220) справедлив только
после окончания переходного процесса
в системе (рис. 2.85).
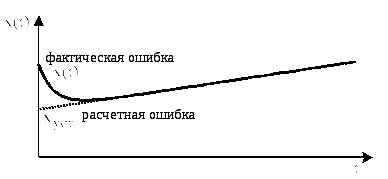
Рисунок 2.85
