2.9. Точность сау в установившихся режимах

Существует два вида установившихся (стационарных) режимов САУ – статический и динамический.

Статический стационарный режим характеризуется тем, что все внешние воздействия и параметры самой системы не изменяются во времени.

Динамический стационарный режим – режим, при котором приложенные к системе внешние воздействия изменяются по некоторому установившемуся закону, в результате чего система переходит в режим установившегося вынужденного движения.

Критерием качества работы САУ в установившемся режиме служат ошибки, вызванные задающим и возмущающим воздействиями.

Будем анализировать точность САУ на примере структурной схемы (рис. 2.79).

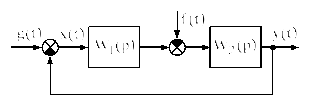
Рисунок 2.79

На рисунке: – передаточная функция регулятора,

–передаточная функция объекта управления.

Пусть

, (2.179)

где , (2.180)

–нормированные полиномы (с равным единице свободным членом). (2.181)

2.9.1. Точность сау в статическом стационарном режиме

Как уже отмечалось ранее, в этом режиме внешние воздействия

, .

2.9.1.1. Система управления с пропорциональным регулятором. Пусть

. (2.182)

Тогда передаточная функция прямой цепи (смотри (2.139)) принимает вид

, (2.183)

где – коэффициент передачи разомкнутой цепи.

В соответствии с формулами (2.138), (2.179), (2.182) и (2.183) изображение ошибки регулирования

, (2.184)

где ;(изображения постоянных величин).

После простых преобразований выражения (2.184) получим изображение составляющей ошибки от задающего воздействия:

. (2.185)

Поскольку знаменатель в формуле (2.185) имеет сомножитель p, то, согласно теореме разложения, ошибка содержит установившуюся (принужденную) составляющую

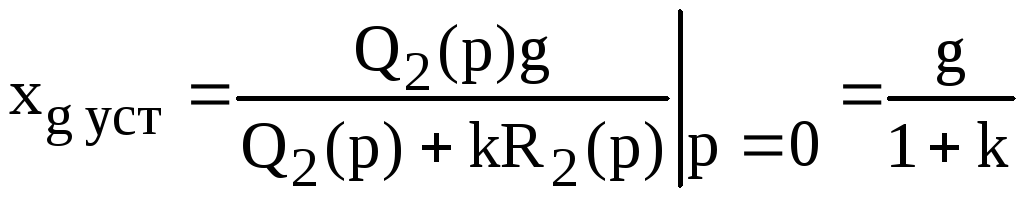. (2.186)

Изображение составляющей ошибки от возмущающего воздействия также получается из выражения (2.184):

. (2.187)

В соответствии с теоремой разложения, принужденная составляющая ошибки будет

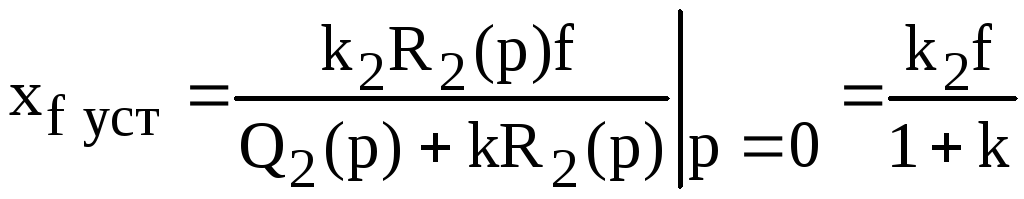. (2.188)

Окончательно в системе управления с П-регулятором установившаяся (статическая) ошибка

. (2.189)

Таким образом, пропорциональный регулятор создает постоянную статическую ошибку, которая тем меньше, чем больше коэффициент усиления разомкнутой САУ. Однако с увеличением k уменьшаются запасы устойчивости по амплитуде и фазе (см. рис. 2.76), и при k, большем некоторого граничного значения, система оказывается неустойчивой. Всегда существует противоречие между точностью и устойчивостью, и необходимо находить компромиссное решение.

2.9.1.2. Система управления с регулятором вида

, (2.190)

где ;– нормированные полиномы (с равным единице свободным членом).

Особенностью регулятора (2.190) является то, что он не содержит интегральную составляющую преобразования ошибки регулирования в управляющее воздействие.

Передаточная функция прямой цепи

. (2.191)

В соответствии с формулами (2.179), (2.184) и (2.191) изображение ошибки регулирования

, (2.192)

где– (2.193) – характеристический полином замкнутой САУ с регулятором.

Нетрудно убедиться, что и в этом случае установившаяся (статическая) ошибка САУ повторяет результат (2.189).

Таким образом, рассмотренные САУ с регуляторами (2.182) и (2.190) являются статическими относительно задающего воздействия и возмущения.

2.9.1.3. Система управления с интегральным регулятором. Пусть . (2.194)

Тогда передаточная функция прямой цепи принимает вид

. (2.195)

В соответствии с формулами (2.179), (2.184) и (2.195) изображение ошибки регулирования

(2.196)

или

, (2.197)

где –характеристический полином (2.198) замкнутой САУ с регулятором (2.194).

Согласно теореме разложения, принужденная составляющая ошибки отсутствует:

. (2.199)

Следовательно, данная САУ с интегральным регулятором является астатической относительно задающего воздействия и возмущения.

Поскольку в передаточной функции разомкнутой САУ (2.195) величина (смотри (2.154)), то говорят: «Система с астатизмом первого порядка».

Таким образом, интегральный регулятор обеспечивает астатизм системы. Однако при этом регулятор вносит дополнительный фазовый сдвиг , что приводит к уменьшению запасов устойчивости по амплитуде и фазе.

Кроме того, интегральное регулирование не обеспечивает астатизм системы относительно всех возмущений.

Пусть, например, в рассматриваемой системе с интегральным регулятором появилось дополнительное возмущение (рис. 2.80).

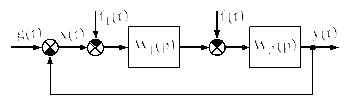
Рисунок 2.80

Изображение составляющей ошибки относительно возмущения будет

. (2.200)

В соответствии с теоремой разложения, принужденная составляющая ошибки будет

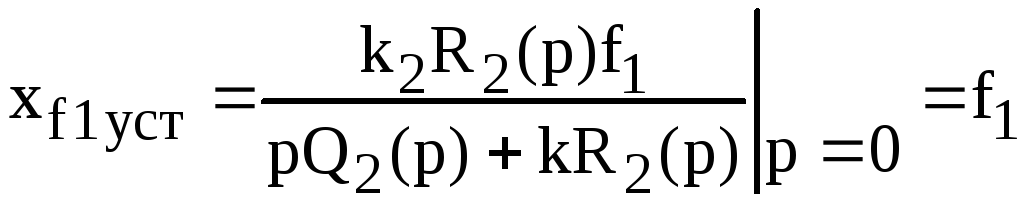, (2.201)

т.е. система является статической относительно возмущения .

Для того чтобы интегральный регулятор мог устранить статическую ошибку от действия какого-либо возмущения, необходимо, чтобы интегратор был включен в прямую цепь передачи управляющего воздействия на ОУ до места приложения данного возмущения (левее).

Отсюда ясно, что интегральный регулятор принципиально не способен устранить ошибку элемента сравнения, которую можно рассматривать как возмущение.

2.9.1.4 Система управления (рис. 2.79) с регулятором вида

. (2.202)

Данный регулятор содержит интегральную составляющую преобразования ошибки регулирования в управляющее воздействие.

Передаточная функция прямой цепи имеет вид

. (2.203)

В соответствии с формулами (2.179), (2.184) и (2.203) изображение ошибки регулирования

(2.204)

или

, (2.205)

где – характеристический полином замкнутой САУ с регулятором (2.202). (2.206)

Согласно теореме разложения, принужденная составляющая ошибки отсутствует:

. (2.207)

По-прежнему система обладает астатизмом первого порядка относительно задающего воздействия и возмущения.